Introduction
Think of a maze in which you are now alone; your aim is to come out as faster as possible but how many ways are there? Now imagine, if you are given a map where you can highlight areas which are worth pursuing and which ones are not! That’s exactly the part heuristic functions serve in algorithms of artificial intelligence. These intelligent instruments assist the AI systems to arrive at better and more prompt decisions, thus deeply simplifying the performance complexity. In this article, we shall discuss the concept of Heuristic function and its place in AI and how these make a massive difference in the time taken to solve problems by how much they enhance the efficiency – making them indispensable in the shelf of tools that coming with Artificial Intelligence.

Learning Outcomes
- Comprehend how heuristic functions work with AI and its role in search algorithms.
- Find out how AI problem solving is improved by the use of heuristic functions.
- See what types of heuristic functions can be found in AI and how they are used.
- Reveal the issues and drawbacks related to heuristic functions.
- Understand ways of evaluation and optimization of heuristic functions in AI.
Table of contents
What is a Heuristic Function?
A heuristic function estimates the cost or distance between a specific state and the goal in a search strategy. It provides a way to select the most promising paths, increasing the likelihood of an effective solution. In other words, a heuristic function gives the algorithm guidance on which direction to take, helping it reach the goal with fewer steps. By doing so, it minimizes the search space and improves the efficiency of the search process.
Types of Heuristic Functions
Heuristic functions come in various forms depending on their ability to estimate the cost and their impact on algorithm performance. Let’s explore these types in detail:
Admissible Heuristics
An admissible heuristic is one that never overestimates the actual cost of reaching the goal. It always provides a lower or equal estimate, ensuring the algorithm can find the shortest path. This type of heuristic is crucial in algorithms like A*, where finding the optimal solution is necessary.
Example: In the A* algorithm, a heuristic that estimates the straight-line distance (Euclidean distance) from one node to another is admissible, as it doesn’t overestimate the true path.
Inadmissible Heuristics
Exogenous inadmissible heuristics can overestimate the cost needed to reach the goal. Although they may not always provide the best solutions, they are valuable when speed is more important than quality.
Example: There are some cases where an inadmissible heuristic can be beneficial in terms of the amount of computation performed, and obtain a non-optimal solution.
Consistent (or Monotonic) Heuristics
A heuristic is admissible if, for every node, the estimated cost to the goal node is no more than the cost of moving from the node to an adjacent node and then to the goal node from the neighbor. Admissible heuristics include consistent heuristics and guarantee that the estimated cost decreases as the algorithm progresses towards the goal.
Example: In a maze-solving problem, the cost of getting from one room to an adjacent room should prove prohibitively high, at least as compared with getting from the previous room and then into the goal room.
Dominating Heuristics
A dominating heuristic is a stronger heuristic function that dominates another if it provides higher values without overestimating the cost. The better the heuristic, the fewer paths the algorithm needs to explore.
Example: In graph traversal, a heuristic estimating both straight-line distance and terrain difficulty would dominate a heuristic that only considers straight-line distance.
Path Finding with Heuristic Functions
Heuristic functions are quite vital in path finding algorithms such as the A* (A-star) which finds great application in GPS navigation, robotics, and gaming among others. Now, let’s illustrate the use of heuristic function in the A* algorithm for path finding step by step. We will describe it with code sample and further describe what heuristic functions do to make the search better.
Problem Setup
We will encode a grid where empty spaces are represented by 0 and walls or any form of obstruction is represented by 1. The purpose of the task is to go from the initial position (the top left of the graph) to the final state (the bottom right of the graph) while being unable to pass through obstacles. This heuristic function will be used to control the path that the algorithm will choose.
Heuristic Function: Euclidean Distance
In this example, we use the Euclidean distance as our heuristic. This heuristic estimates the cost from the current node to the goal node as the straight-line distance, calculated as:
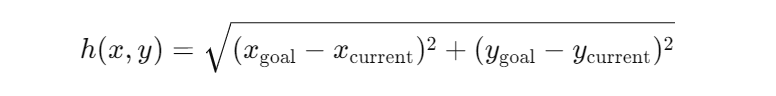
This function gives the algorithm an estimate of how far a node is from the goal, helping it prioritize which node to explore next.
Detailed Walkthrough of the A Algorithm with Heuristic Function*
Let us explore basic steps of A* algorithm heuristic function.
Step1: Heuristic Function
The heuristic function (Euclidean distance) is critical in the A* algorithm. It helps estimate the “distance” from the current node to the goal. By using the heuristic value, the algorithm can prioritize nodes that are more likely to lead to the goal, reducing the total number of nodes explored.
Step2: Exploring Neighbors
The A* algorithm explores neighboring nodes by checking each possible movement direction. If a neighbor is within the bounds of the grid and isn’t blocked by an obstacle, it is added to the open_list for further exploration.
Step3: Prioritizing Nodes
The open_list is a priority queue that keeps track of nodes based on their total estimated cost (f = g + h). This ensures that nodes closer to the goal (in terms of the heuristic) are explored first.
Step4: Path Reconstruction
Once the algorithm reaches the goal node, it traces the path back to the start node using the came_from dictionary. This provides the shortest path, which is then printed.
Grid Representation and Heuristic Function
First, we represent the grid and define the heuristic function, which estimates the cost from the current node to the goal node. We’ll use the Euclidean distance as our heuristic.
import math
# Heuristic function: Euclidean distance
def heuristic(node, goal):
return math.sqrt((goal[0] - node[0])**2 + (goal[1] - node[1])**2)
# Example grid (0 = free, 1 = obstacle)
grid = [
[0, 0, 0, 1, 0],
[0, 1, 0, 1, 0],
[0, 1, 0, 0, 0],
[0, 0, 1, 1, 0],
[1, 0, 0, 0, 0]
]
start = (0, 0) # Starting point (top-left corner)
goal = (4, 4) # Goal point (bottom-right corner)A Algorithm Setup*
Next, we set up the A* algorithm by initializing the necessary variables and structures:
- Priority Queue (
open_list): This stores nodes that need to be explored. - Cost Tracking (
cost_so_far): This dictionary keeps track of the cost from the start node to each explored node. - Path Tracking (
came_from): This helps reconstruct the path once we reach the goal.
import heapq
# A* algorithm implementation
def astar(grid, start, goal):
# Directions for movement (up, down, left, right, and diagonals)
directions = [(-1, 0), (1, 0), (0, -1), (0, 1), (-1, -1), (-1, 1), (1, -1), (1, 1)]
# Priority queue to store nodes for exploration
open_list = []
heapq.heappush(open_list, (0 + heuristic(start, goal), 0, start))
# Tracking the cheapest cost to reach each node
came_from = {}
cost_so_far = {start: 0}
# A* algorithm loop
while open_list:
# Get the node with the lowest total cost (g + h)
current_f, current_g, current_node = heapq.heappop(open_list)
# Check if we've reached the goal
if current_node == goal:
return reconstruct_path(came_from, start, goal)
# Explore neighbors
for direction in directions:
neighbor = (current_node[0] + direction[0], current_node[1] + direction[1])
# Check if the neighbor is within bounds and not an obstacle
if 0 <= neighbor[0] < len(grid) and 0 <= neighbor[1] < len(grid[0]) and grid[neighbor[0]][neighbor[1]] == 0:
new_cost = cost_so_far[current_node] + 1 # Assume movement cost is 1
# If the neighbor is unvisited or a cheaper path is found
if neighbor not in cost_so_far or new_cost < cost_so_far[neighbor]:
cost_so_far[neighbor] = new_cost
f_score = new_cost + heuristic(neighbor, goal)
heapq.heappush(open_list, (f_score, new_cost, neighbor))
came_from[neighbor] = current_node
return [] # Return an empty list if no path is foundReconstructing the Path
Once we reach the goal, we need to reconstruct the path from the start to the goal using the came_from dictionary. This dictionary tracks where we came from for each node.
# Function to reconstruct the path from start to goal
def reconstruct_path(came_from, start, goal):
current = goal
path = [current]
while current != start:
current = came_from[current]
path.append(current)
path.reverse()
return pathRunning the A* Algorithm
Finally, we execute the A* algorithm using the astar() function and print the path found.
# Running the A* algorithm to find the path
path = astar(grid, start, goal)
if path:
print("Path found:", path)
else:
print("No path found.")Example Output:
Path found: [(0, 0), (1, 0), (2, 0), (3, 1), (4, 2), (4, 3), (4, 4)]Role of Heuristic Functions in AI
Heuristic functions play a critical role in AI, especially in search algorithms where they guide the decision-making process. Here’s a breakdown of their key roles:
Guiding Search Algorithms
Heuristic functions act as a compass for search algorithms by estimating the cost from the current state to the goal. This estimation helps algorithms focus on more promising paths, reducing the time and effort required to explore less fruitful options. In algorithms like A*, the heuristic function significantly accelerates the search by prioritizing nodes that are likely to lead to a solution.
Reducing Computational Complexity
Heuristic functions are important as failure may occur in which several options exist and the number increases exponentially with the expansion of the problem. Heuristics reduce this problem by sampling only the most plausible paths of search space since arbitrary paths lead to arbitrary solutions. This reduction in complexity is very important especially in the applications requiring real time solutions such as robotics.
Enhancing Problem-Solving Efficiency
Heuristic functions help search algorithms by providing specific information about the problem. This allows the algorithm to make educated guesses rather than trying all possible solutions. As a result, it leads to more efficient problem-solving in real-world situations. Heuristics are especially important in large-scale AI challenges like games, navigation, and optimization. They play a vital role in tackling complex problems more effectively.
Balancing Accuracy and Speed
Sometimes, heuristic functions are designed to be less accurate but faster than other algorithms. While admissible heuristics guarantee the identification of the shortest path, inadmissible heuristics provide near-optimal solutions more quickly. Indeed, this balance of optimization with regards to speed is particularly relevant in situations in which it is essential to find a solution fast rather than to focus on achieving an optimal solution.
Adapting to Domain-Specific Challenges
Heuristic functions are usually defined based on the specific problem domain. They rely on knowledge about the problems and objectives of the task. Because of this, they are useful in many AI applications. They help with route planning in design AIs and assessing options in game AIs.
Importance of Heuristic Functions in AI
Heuristic functions are essential to AI, especially when solving problems that involve large search spaces. Without heuristics, search algorithms would have to explore every possible solution, causing an exponential increase in time and computational resources. Here’s why they are critical:
- Efficiency: Heuristic functions dramatically reduce the number of paths an algorithm needs to evaluate. By guiding the algorithm toward the most promising routes, they cut down both time and space complexity, allowing AI systems to find solutions faster.
- Scalability: In case of actual applications like route finding, games and optimization, the size of the search domain can be enormous. Approximations assist in the scaling of the algorithms towards other larger problems for they only explore paths that will likely provide solutions rather than exploring the whole search space.
- Problem-Specific Insight: Heuristic functions leverage knowledge of the problem domain to become highly effective for specific issues. For example, in game AI, developers create heuristics to evaluate moves based on game rules, thereby enhancing decision-making during gameplay.
Applications of Heuristic Functions
Let us explore applications of Heuristic Functions below:
- Pathfinding Algorithms: Heuristic functions are widely used in pathfinding algorithms like A* and Dijkstra’s algorithm. In these algorithms, heuristics help estimate the shortest path between two points in a graph, making them essential in applications like GPS navigation systems.
- Game AI: In games like chess, heuristic functions evaluate the potential outcomes of different moves, helping the AI choose the most strategic options. These functions are crucial in scenarios where calculating all possible moves is computationally infeasible.
- Optimization Problems: Heuristics are employed in optimization problems, such as the traveling salesman problem, to find near-optimal solutions within a reasonable time frame. While these functions may not guarantee the optimal solution, they often provide solutions that are close enough for practical purposes.
- Constraint Satisfaction Problems: In problems like scheduling and resource allocation, heuristic functions guide the search for solutions that satisfy all constraints, improving the efficiency of the search process.
Challenges and Limitations
Despite their effectiveness, heuristic functions come with challenges that limit their application:
Design Complexity
One of the biggest challenges is designing an effective heuristic. A heuristic must accurately estimate the cost to the goal without being too conservative or too aggressive. A poorly designed heuristic can lead to inefficient searches or suboptimal solutions.
Problem-Specific Nature
Heuristic functions are often tailored to specific problems, which limits their generalization. A heuristic that works well for a particular scenario may not be applicable in a different context, requiring the design of new heuristics for each problem.
Computational Overhead
While heuristics reduce search space, calculating a complex heuristic at each step can introduce computational overhead. If the cost of computing the heuristic outweighs its benefits, it may not improve overall performance.
Risk of Suboptimal Solutions
Inadmissible heuristics, while faster, risk leading to suboptimal solutions. AI applications that require precision must carefully consider the trade-off between speed and accuracy.
Conclusion
Heuristic functions are crucial in AI. They form the backbone of many search algorithms and problem-solving techniques. By offering informed estimates, they help algorithms navigate complex search spaces efficiently. This makes AI systems more effective and practical in real-world applications. However, designing and optimizing heuristic functions require careful thought. Their effectiveness can greatly impact the performance of AI algorithms.
Frequently Asked Questions
A. In AI, a heuristic function estimates the cost or distance from a current state to a goal state, guiding search algorithms in their decision-making.
A. Heuristic functions are important because they help AI algorithms efficiently navigate complex search spaces by prioritizing the most promising paths.
A. Admissible heuristics are functions that never overestimate the cost to reach the goal, ensuring that the algorithm finds the shortest path.
A. Not always. While admissible heuristics guarantee optimal solutions, inadmissible heuristics may lead to suboptimal solutions but can offer faster results in certain scenarios.
A. People commonly use heuristic functions in pathfinding, game AI, optimization problems, and constraint satisfaction problems.





