What is an Eigenvector and Eigenvalues?

Linear algebra is a cornerstone of many advanced mathematical concepts and is extensively used in data science, machine learning, computer vision, and engineering. One of the fundamental concepts in linear algebra is eigenvectors, often paired with eigenvalues. But what exactly is an eigenvector, and why is it so important?

This article breaks down the concept of eigenvectors in a simple and intuitive manner, making it easy for anyone to grasp.

What is an Eigenvector?

A square matrix is associates with a special type of vector called an eigenvector. When the matrix acts on the eigenvector, it keeps the direction of the eigenvector unchanged and only scales it by a scalar value called the eigenvalue.

In mathematical terms, for a square matrix A, a non-zero vector v is an eigenvector if:

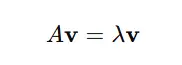
Here:

• A is the matrix.
• v is the eigenvector.
• λ is the eigenvalue (a scalar).

Intuition Behind Eigenvectors

Imagine you have a matrix A representing a linear transformation, such as stretching, rotating, or scaling a 2D space. When this transformation is applied to a vector v:

• Most vectors will change their direction and magnitude.
• Some special vectors, however, will only be scaled but not rotated or flipped. These special vectors are eigenvectors.

For example:

• If λ>1, the eigenvector is stretched.
• If 0<λ<1, the eigenvector is compressed.
• If λ=−1, the eigenvector flips its direction but maintains the same length.

Why Are Eigenvectors Important?

Eigenvectors play a crucial role in various mathematical and real-world applications:

1. Principal Component Analysis (PCA): PCA is a widely used technique for dimensionality reduction. Eigenvectors are used to determine the principal components of the data, which capture the maximum variance and help identify the most important features.
2. Google PageRank: The algorithm that ranks web pages uses eigenvectors of a matrix representing the links between web pages. The principal eigenvector helps determine the relative importance of each page.
3. Quantum Mechanics: In physics, eigenvectors and eigenvalues describe the states of a system and their measurable properties, such as energy levels.
4. Computer Vision: Eigenvectors are used in facial recognition systems, particularly in techniques like Eigenfaces, where they help represent images as linear combinations of significant features.
5. Vibrational Analysis: In engineering, eigenvectors describe the modes of vibration in structures like bridges and buildings.

How to Compute Eigenvectors?

To find eigenvectors, follow these steps:

• Set up the eigenvalue equation: Start with Av=λv and rewrite it as (A−λI)v=0, where I is the identity matrix. Solve for eigenvalues: Find eigenvectors:
• Solve for eigenvalues: Compute det⁡(A−λI)=0 to find the eigenvalues λ.
• Find eigenvectors: Substitute each eigenvalue λ into (A−λI)v=0 and solve for v.

Example: Eigenvectors in Action

Consider a matrix:

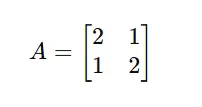
Step 1: Find eigenvalues λ.

Solve det⁡(A−λI)=0:

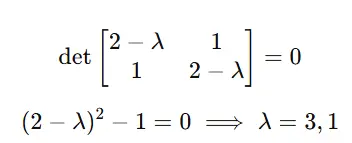
Step 2: Find eigenvectors for each λ.

For λ=3:

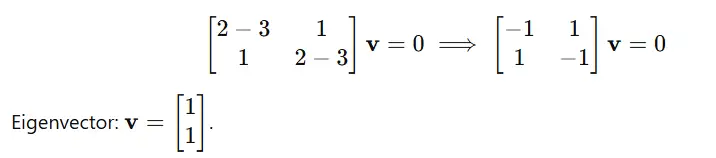
For λ=1:

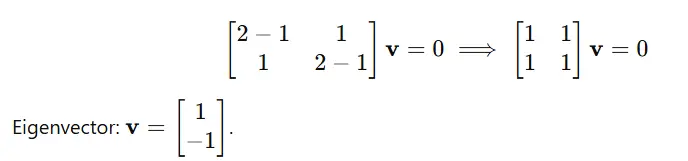
Python Implementation

Let’s compute the eigenvalues and eigenvectors of a matrix using Python.

Example Matrix

Consider the matrix:

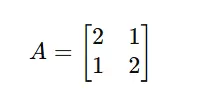
Code Implementation

import numpy as np

# Define the matrix
A = np.array([[2, 1], [1, 2]])

# Compute eigenvalues and eigenvectors
eigenvalues, eigenvectors = np.linalg.eig(A)

# Display results
print("Matrix A:")
print(A)

print("\nEigenvalues:")
print(eigenvalues)

print("\nEigenvectors:")
print(eigenvectors)

Output:

Matrix A:
[[2 1]
 [1 2]]

Eigenvalues:
[3. 1.]

Eigenvectors:
[[ 0.70710678 -0.70710678]
 [ 0.70710678  0.70710678]]

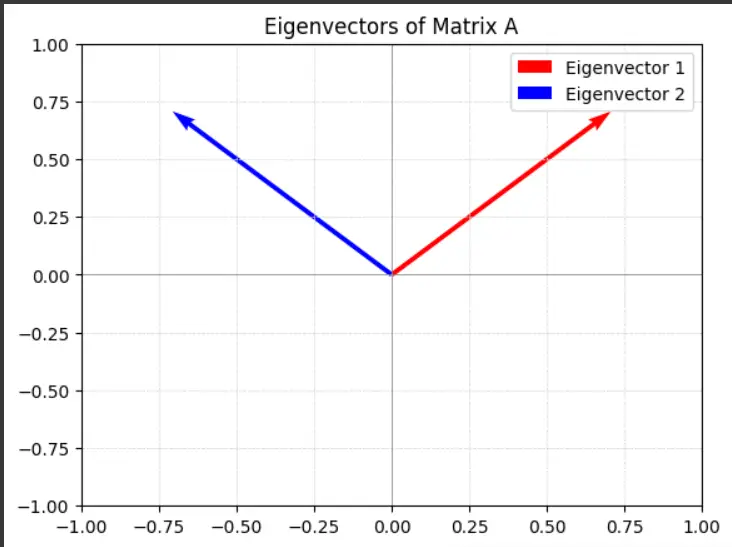
Visualizing Eigenvectors

You can visualize how eigenvectors behave under the transformation defined by matrix A.

Visualization Code

import matplotlib.pyplot as plt

# Define eigenvectors
eig_vec1 = eigenvectors[:, 0]
eig_vec2 = eigenvectors[:, 1]

# Plot original eigenvectors
plt.quiver(0, 0, eig_vec1[0], eig_vec1[1], angles='xy', scale_units='xy', scale=1, color='r', label='Eigenvector 1')
plt.quiver(0, 0, eig_vec2[0], eig_vec2[1], angles='xy', scale_units='xy', scale=1, color='b', label='Eigenvector 2')

# Adjust plot settings
plt.xlim(-1, 1)
plt.ylim(-1, 1)
plt.axhline(0, color='gray', linewidth=0.5)
plt.axvline(0, color='gray', linewidth=0.5)
plt.grid(color='lightgray', linestyle='--', linewidth=0.5)
plt.legend()
plt.title("Eigenvectors of Matrix A")
plt.show()

This code will produce a plot showing the eigenvectors of AAA, illustrating their directions and how they remain unchanged under the transformation.

Key Takeaways

• Eigenvectors are special vectors that remain in the same direction when transformed by a matrix.
• They are paired with eigenvalues, which determine how much the eigenvectors are scaled.
• Eigenvectors have significant applications in data science, machine learning, engineering, and physics.
• Python provides tools like NumPy to compute eigenvalues and eigenvectors easily.

Conclusion

Eigenvectors are a cornerstone concept in linear algebra, with far-reaching applications in data science, engineering, physics, and beyond. They represent the essence of how a matrix transformation affects certain special directions, making them indispensable in areas like dimensionality reduction, image processing, and vibrational analysis.

By understanding and computing eigenvectors, you unlock a powerful mathematical tool that enables you to solve complex problems with clarity and precision. With Python’s robust libraries like NumPy, exploring eigenvectors becomes straightforward, allowing you to visualize and apply these concepts in real-world scenarios.

Whether you’re building machine learning models, analyzing structural dynamics, or diving into quantum mechanics, a solid understanding of eigenvectors is a skill that will serve you well in your journey.

Frequently Asked Questions

Janvi Kumari

Hi, I am Janvi, a passionate data science enthusiast currently working at Analytics Vidhya. My journey into the world of data began with a deep curiosity about how we can extract meaningful insights from complex datasets.