Introduction
Variable selection is an important aspect of model building which every analyst must learn. After all, it helps in building predictive models free from correlated variables, biases and unwanted noise.
A lot of novice analysts assume that keeping all (or more) variables will result in the best model as you are not losing any information. Sadly, that is not true!
How many times has it happened that removing a variable from the model has increased your model accuracy ?
At least, it has happened to me. Such variables are often found to be correlated and hinder achieving higher model accuracy. Today, we’ll learn one of the ways of how to get rid of such variables in R. I must say, R has an incredible CRAN repository. Out of all packages, one such available package for variable selection is Boruta Package.
In this article, we’ll focus on understanding the theory and practical aspects of using Boruta Package. I’ve followed a step wise approach to help you understand better.
I’ve also drawn a comparison of boruta with other traditional feature selection algorithms. Using this, you can arrive at a more meaningful set of features which can pave the way for a robust prediction model. The terms “features”, “variables” and “attributes” have been used interchangeably, so don’t get confused!

What is Boruta algorithm and why such a strange name ?
Boruta is a feature selection algorithm. Precisely, it works as a wrapper algorithm around Random Forest. This package derive its name from a demon in Slavic mythology who dwelled in pine forests.
We know that feature selection is a crucial step in predictive modeling. This technique achieves supreme importance when a data set comprised of several variables is given for model building.
Boruta can be your algorithm of choice to deal with such data sets. Particularly when one is interested in understanding the mechanisms related to the variable of interest, rather than just building a black box predictive model with good prediction accuracy.
How does it work?
Below is the step wise working of boruta algorithm:
- Firstly, it adds randomness to the given data set by creating shuffled copies of all features (which are called shadow features).
- Then, it trains a random forest classifier on the extended data set and applies a feature importance measure (the default is Mean Decrease Accuracy) to evaluate the importance of each feature where higher means more important.
- At every iteration, it checks whether a real feature has a higher importance than the best of its shadow features (i.e. whether the feature has a higher Z score than the maximum Z score of its shadow features) and constantly removes features which are deemed highly unimportant.
- Finally, the algorithm stops either when all features gets confirmed or rejected or it reaches a specified limit of random forest runs.
What makes it different from traditional feature selection algorithms?
Boruta follows an all-relevant feature selection method where it captures all features which are in some circumstances relevant to the outcome variable. In contrast, most of the traditional feature selection algorithms follow a minimal optimal method where they rely on a small subset of features which yields a minimal error on a chosen classifier.
While fitting a random forest model on a data set, you can recursively get rid of features in each iteration which didn’t perform well in the process. This will eventually lead to a minimal optimal subset of features as the method minimizes the error of random forest model. This happens by selecting an over-pruned version of the input data set, which in turn, throws away some relevant features.
On the other hand, boruta find all features which are either strongly or weakly relevant to the decision variable. This makes it well suited for biomedical applications where one might be interested to determine which human genes (features) are connected in some way to a particular medical condition (target variable).
Boruta in Action in R (Practical)
Till here, we have understood the theoretical aspects of Boruta Package. But, that isn’t enough. The real challenge starts now. Let’s learn to implement this package in R.
First things first. Let’s install and call this package for use.
> install.packages("Boruta")
> library(Boruta)
Now, we’ll load the data set. For this tutorial I’ve taken the data set from Practice Problem Loan Prediction
> setwd("../Data/Loan_Prediction")
> traindata <- read.csv("train.csv", header = T, stringsAsFactors = F)
Let’s have a look at the data.
> str(traindata)
> names(traindata) <- gsub("_", "", names(traindata))
gsub() function is used to replace an expression with other one. In this case, I’ve replaced the underscore(_) with blank(“”).
Let’s check if this data set has missing values.
> summary(traindata)
We find that many variables have missing values. It’s important to treat missing values prior to implementing boruta package. Moreover, this data set also has blank values. Let’s clean this data set.
Now we’ll replace blank cells with NA. This will help me treat all NA’s at once.
> traindata[traindata == ""] <- NA
Here, I’m following the simplest method of missing value treatment i.e. list wise deletion. More sophisticated methods & packages of missing value imputation can be found here.
> traindata <- traindata[complete.cases(traindata),]
Let’s convert the categorical variables into factor data type.
> convert <- c(2:6, 11:13)
> traindata[,convert] <- data.frame(apply(traindata[convert], 2, as.factor))
Now is the time to implement and check the performance of boruta package. The syntax of boruta is almost similar to regression (lm) method.
> set.seed(123)
> boruta.train <- Boruta(LoanStatus~.-LoanID, data = traindata, doTrace = 2)
> print(boruta.train)
Boruta performed 99 iterations in 18.80749 secs.
5 attributes confirmed important: ApplicantIncome, CoapplicantIncome,
CreditHistory, LoanAmount, LoanAmountTerm.
4 attributes confirmed unimportant: Dependents, Education, Gender, SelfEmployed.
2 tentative attributes left: Married, PropertyArea.
Boruta gives a crystal clear call on the significance of variables in a data set. In this case, out of 11 attributes, 4 of them are rejected and 5 are confirmed. 2 attributes are designated as tentative. Tentative attributes have importance so close to their best shadow attributes that Boruta is not able to make a decision with the desired confidence in default number of random forest runs.
Now, we’ll plot the boruta variable importance chart.
By default, plot function in Boruta adds the attribute values to the x-axis horizontally where all the attribute values are not dispayed due to lack of space.
Here I’m adding the attributes to the x-axis vertically.
> plot(boruta.train, xlab = "", xaxt = "n")
> lz<-lapply(1:ncol(boruta.train$ImpHistory),function(i)
boruta.train$ImpHistory[is.finite(boruta.train$ImpHistory[,i]),i])
> names(lz) <- colnames(boruta.train$ImpHistory)
> Labels <- sort(sapply(lz,median))
> axis(side = 1,las=2,labels = names(Labels),
at = 1:ncol(boruta.train$ImpHistory), cex.axis = 0.7)
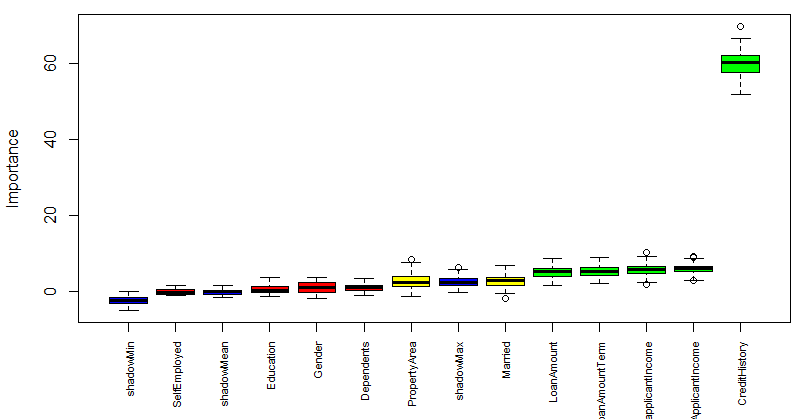
Blue boxplots correspond to minimal, average and maximum Z score of a shadow attribute. Red, yellow and green boxplots represent Z scores of rejected, tentative and confirmed attributes respectively.
Now is the time to take decision on tentative attributes. The tentative attributes will be classified as confirmed or rejected by comparing the median Z score of the attributes with the median Z score of the best shadow attribute. Let’s do it.
> final.boruta <- TentativeRoughFix(boruta.train)
> print(final.boruta)
Boruta performed 99 iterations in 18.399 secs.
Tentatives roughfixed over the last 99 iterations.
6 attributes confirmed important: ApplicantIncome, CoapplicantIncome,
CreditHistory, LoanAmount, LoanAmountTerm and 1 more.
5 attributes confirmed unimportant: Dependents, Education, Gender, PropertyArea,
SelfEmployed.
Boruta result plot after the classification of tentative attributes
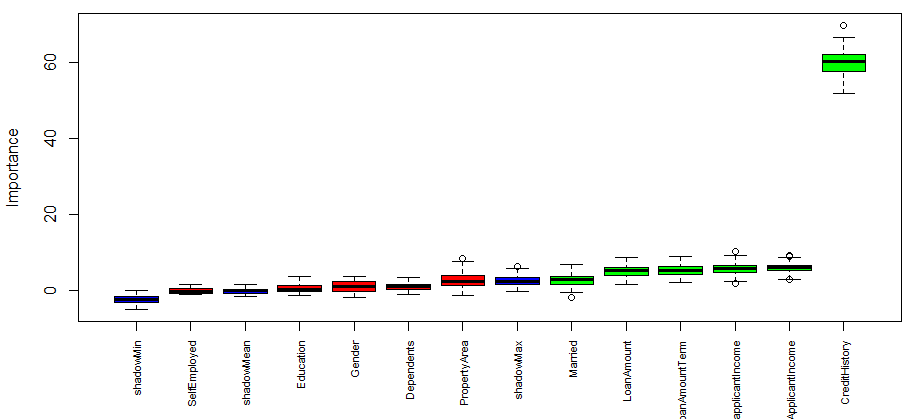
It’s time for results now. Let’s obtain the list of confirmed attributes
> getSelectedAttributes(final.boruta, withTentative = F)
[1] "Married" "ApplicantIncome" "CoapplicantIncome" "LoanAmount"
[5] "LoanAmountTerm" "CreditHistory"
We’ll create a data frame of the final result derived from Boruta.
> boruta.df <- attStats(final.boruta)
> class(boruta.df)
[1] "data.frame"
> print(boruta.df)
meanImp medianImp minImp maxImp normHits decision
Gender 1.04104738 0.9181620 -1.9472672 3.767040 0.01010101 Rejected
Married 2.76873080 2.7843600 -1.5971215 6.685000 0.56565657 Confirmed
Dependents 1.15900910 1.0383850 -0.7643617 3.399701 0.01010101 Rejected
Education 0.64114702 0.4747312 -1.0773928 3.745441 0.03030303 Rejected
SelfEmployed -0.02442418 -0.1511711 -0.9536783 1.495992 0.00000000 Rejected
ApplicantIncome 6.05487791 6.0311639 2.9801751 9.197305 0.94949495 Confirmed
CoapplicantIncome 5.76704389 5.7920332 1.9322989 10.184245 0.97979798 Confirmed
LoanAmount 5.19167613 5.3606935 1.7489061 8.855464 0.88888889 Confirmed
LoanAmountTerm 5.50553498 5.3938036 2.0361781 9.025020 0.90909091 Confirmed
CreditHistory 59.57931404 60.2352549 51.7297906 69.721650 1.00000000 Confirmed
PropertyArea 2.77155525 2.4715892 -1.2486696 8.719109 0.54545455 Rejected
Let’s understand the parameters used in Boruta as follows:
- maxRuns: maximal number of random forest runs. You can consider increasing this parameter if tentative attributes are left. Default is 100.
- doTrace: It refers to verbosity level. 0 means no tracing. 1 means reporting attribute decision as soon as it is cleared. 2 means all of 1 plus additionally reporting each iteration. Default is 0.
- holdHistory: The full history of importance runs is stored if set to TRUE (Default). Gives a plot of Classifier run vs. Importance when the plotImpHistory function is called.
For more complex parameters, please refer to the package documentation of Boruta.
Boruta vs Traditional Feature Selection Algorithm
Till here, we have learnt about the concept and steps to implement boruta package in R.
What if we used a traditional feature selection algorithm such as recursive feature elimination on the same data set. Do we end up with the same set of important features? Let us find out.
Now, we’ll learn the steps used to implement recursive feature elimination (RFE). In R, RFE algorithm can be implemented using caret package.
Let’s start by defining a control function to be used with RFE algorithm. We’ll load the required libraries:
> library(caret)
> library(randomForest)
> set.seed(123)
> control <- rfeControl(functions=rfFuncs, method="cv", number=10)
Here we have specified a random forest selection function through rfFuncs option (which is also the underlying algorithm in Boruta)
Let’s implement the RFE algorithm now.
> rfe.train <- rfe(traindata[,2:12], traindata[,13], sizes=1:12, rfeControl=control)
I’m sure this is self explanatory. traindata[,2:12] refers to selecting all independent variables except the ID variable. traindata[,13] selects only the dependent variable. It might take some time to run.
We can also check the outcome of this algorithm.
> rfe.train
Recursive feature selection
Outer resampling method: Cross-Validated (10 fold)
Resampling performance over subset size:
Variables Accuracy Kappa AccuracySD KappaSD Selected
1 0.8083 0.4702 0.03810 0.1157 *
2 0.8041 0.4612 0.03575 0.1099
3 0.8021 0.4569 0.04201 0.1240
4 0.7896 0.4378 0.03991 0.1249
5 0.7978 0.4577 0.04557 0.1348
6 0.7957 0.4471 0.04422 0.1315
7 0.8061 0.4754 0.04230 0.1297
8 0.8083 0.4767 0.04055 0.1203
9 0.7897 0.4362 0.05044 0.1464
10 0.7918 0.4453 0.05549 0.1564
11 0.8041 0.4751 0.04419 0.1336
The top 1 variables (out of 1):
CreditHistory
This algorithm gives highest weightage to Credit History. Now, we’ll plot the result of RFE algorithm and obtain a variable importance chart.
> plot(rfe.train, type=c("g", "o"), cex = 1.0, col = 1:11)
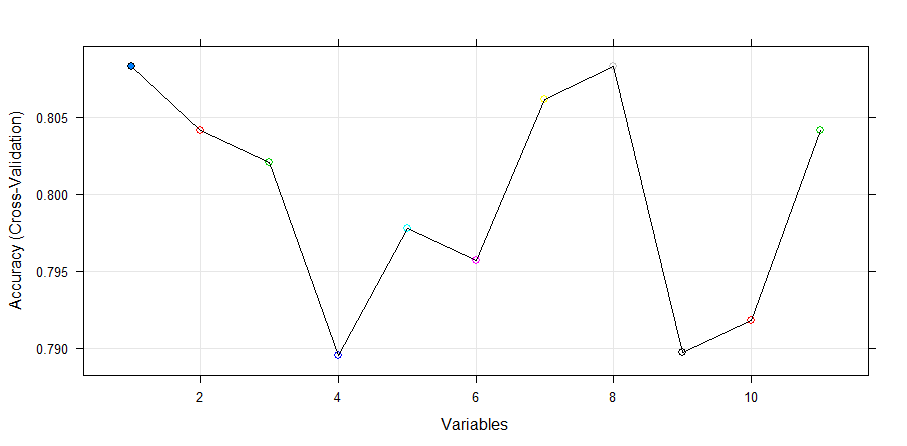
Let’s extract the chosen features. I am confident it would result in Credit History.
> predictors(rfe.train)
[1] "CreditHistory"
Hence, we see that recursive feature elimination algorithm has selected “CreditHistory” as the only important feature among the 11 features in the dataset.
As compared to this traditional feature selection algorithm, boruta returned a much better result of variable importance which was easy to interpret as well ! I find it awesome to work on R where one has access to so many amazing packages. I’m sure there would be many other packages for feature selection. I’d love to read about them.
End notes
Boruta is an easy to use package as there aren’t many parameters to tune / remember. You shouldn’t use a data set with missing values to check important variables using Boruta. It’ll blatantly throw errors. You can use this algorithm on any classification / regression problem in hand to come up with a subset of meaningful features.
In this article, I’ve used a quick method to impute missing value because the scope of this article was to understand boruta (theory & practical). I’d suggest you to use advanced methods of missing value imputation. After all, information available in data is all we look for ! Keep going.
Did you like reading this article ? What other methods of variable selection do you use? Do share your suggestions / opinions in the comments section below.
About the Author
 Debarati Dutta is MA Econometrics graduate from University of Madras. She has more than 3 years of experience in data analytics and predictive modeling across multiple domains. She has worked in companies such as Amazon, Antuit, Netlink. Currently, she’s based out of Montreal, Canada.
Debarati Dutta is MA Econometrics graduate from University of Madras. She has more than 3 years of experience in data analytics and predictive modeling across multiple domains. She has worked in companies such as Amazon, Antuit, Netlink. Currently, she’s based out of Montreal, Canada.
Debarati is the first winner of Blogathon. She won amazon voucher worth INR 5000.







Gr8 Share Debrati. I was looking for the same kind of info. Keep sharing. Thanks.
Thanks Sreenivas. Glad that it helped.
Beautiful, meaningful info, thanks a lot
Thank you so much Dr. Samuel.
Hi, This is not the best package for the determination of the importance of predictors. See this article.https://www.mql5.com/en/articles/2029
Hi Vlad, Thanks for the interesting article. Well, I would say "best" is more likely a relative term which depends a lot on the problem we have in hand as well as our needs. As mentioned in another comment, if prediction accuracy is your only concern, it might / might not be the best method for feature selection. But, if you are also interested in understanding the relationships in your data, it would do a much better job. Hence, application of machine learning techniques involve a lot of trial and error to arrive at the "best" method.