Can we create a flawless winning strategy in a Casino using Data Science?
Of course not! Otherwise, all the data scientists out there would be sitting on piles of cash and the casinos would shut us out!
But, in this article we will learn how to evaluate if a game in Casino is biased or fair. We will understand the biases working in a casino and create strategies to become profitable. We will also learn how can we control the probability of going bankrupt in Casinos.
To make the article interactive, I have added few puzzles in the end to use these strategies. If you can crack them there is no strategy that can make you hedge against loosing in a Casino.
Read on!!
Brain Teaser

Before we begin, let me ask you a couple of questions:
- How many times have you gambled in a Casino till now?
- How many times have you lost all your money in a Casino?
If your answer for second question is more than half of question one, then you fall in same basket as most of the players going to a Casino (and you make them profitable!).
Now here’s an interesting fact, for most of the games you play at a Casino, you will win the amount in line with your odds of winning. For example: If the probability of winning in a roulette table is 1/37, you will get 37X of the amount you had bet. Hence, the expected losses of a trade in Casino is almost equal to zero.
Expected gain from roulette = 1/37 * $X * 37 (amount you get if you win) – $X (amount you bet) = 0
So, where are we going wrong?
Why do our chances of gaining 100% or more are less than 50% but our chances of losing 100% is a lot more than 50%. Let’s start with my recent visit to a Casino.
My recent experience with BlackJack
Last week, I went to Atlantic City – the casino hub of US east coast. BlackJack has always been my favorite game because of a lot of misconceptions.
For the starters, let me take you through how BlackJack is played.
 There are few important things to note about BlackJack. If you know the game, you can skip the points below:
There are few important things to note about BlackJack. If you know the game, you can skip the points below:
- Every card has a value.
-
Ace card is counted as 1 or 11 points, numbered cards (2 to 9) are counted at face value. 10 numbered card and face cards are counted as 10 points.
-
The value of a hand is the sum of the point values of the individual cards. Except, a “blackjack” is the highest hand, consisting of an ace and any 10-point card, and it outranks all other 21-point hands.
-
If the sum exceeds 21, it is called a “burst” and whoever has a burst looses right away.
- After the players have played their bet, the dealer will give two cards to the each player and keeps one card for himself.
-
The dealer will ask the players for any further bet, and a player can choose to double the bet based on his 2 cards and dealer’s 1 card. Then the dealer will ask the player if he/she needs more cards. Player tries to maximize his score without being burst.
-
After the final bet, the dealer will open more card for him/her. Dealer will keep opening his/her cards, until the value reaches 17 (Dealer might have to open another card if he/she has an Ace card counted as 11, and total sum as 17 – this is called soft 17).
- Finally we count players points and dealers points. Higher point wins.
There are a few more complicated concepts like insurance and split, which is beyond the scope of this article. So, we will keep things simple.
I always thought that given the dealer has a constraint of opening cards till he/she reaches 17/18, they cannot stop taking more cards. Hence, a player has better odds of winning than the dealer as he/she has no such constraints. I was excited about all the winning I was about to get!!
As soon as I entered the Casino, I separated $X in my purse as “Casino money”, Got my cash converted into chips, and with in the next hour, I was bankrupt. I was not done yet – In hopes of recovering the money I lost, I donated another $2X in two rounds and I was finally convinced that the game was not as simple as I thought and I needed to pull out my data science hat to win it.
Pre-requisites for the article
Following are a few good to have skills to enjoy the article more:
- Understanding of basic probability will be a plus. I will try not to talk a lot in that language. So if you are scared of probabilities you are fine.
- If you know R, you will be able to run the simulations on your own. No knowledge of R is required to understand the output.
What to expect in this article?
Here are the questions, I will try to answer in this article. They can be broadly classified in three heads:
Category 1 – Gaming Strategy related questions
- What is the probability of a dealer going burst given I know which is the first card of the dealer?
- What is the best strategy for a player if he/she knows his/her first 2 cards and dealer’s 1 face-up card?
- Should the player hold at 2
- Should the player go ahead and take 3rd, 4th, 5th … card
- What is the probability of winning given I know a player’s final score and dealer’s single face-up card?
- What is the probability of winning BlackJack at this point when the cards are yet to be dealt? Is it more than 50% as I thought, or was I terribly wrong?
Category 2 – Betting Strategy
- Why do we lose / become bankrupt most of the time when we gamble in a Casino?
- Is there a betting strategy which can skew our chances of winning?
- When does this betting strategy work and when does it backfire?
- Using such a strategy, can we change the expected value of losses / gain compared to random betting (or single value betting)?
Category 3 – A few Fundamental Questions
- Can we win against Casinos?
- Did I uncover the secret of winning a million dollars in a Casino? I can certainly use that when I go to Casino the next time.
- Is it better to play BlackJack or simply win on a flip of coin/play roulette if the only objective is to win money?
Let’s get the ball rolling
Here is a situation, you see that dealer has a “4” open and following are your cards.

Your total score is “14”. What would you do?
By now, you will know that your cards are really poor but do you take another card and expose yourself to the risk of getting burst OR you will take the chance to stay and let the dealer get burst. A lot of people will recommend you to stay till dealer’s cards are as bad as yours – let us check out through simulations.
Simulation 1
Let us try to calculate the probability of the dealer getting burst. I will first define a few basic functions on R and then simulate dealer’s hand.
####This function will take input as the initial hand and draw a new card. Finally it returns the new full hand
card_draw <- function(dealers_hand_1){
next_card <- sample(deck,1)
dealers_hand_1 <- c(dealers_hand_1,next_card)
return(dealers_hand_1)
}
####This function will find the sum of cards making sure Ace is counted in the right capacity
find_sum <- function(hand){
aces <- hand[hand == 1]
num_aces <- length(aces)
sum_1 <- num_aces*10 + sum(hand)
count <- 1
while(sum_1 > 21 & count < num_aces +1){
sum_1 <- sum_1 - 10
count <- count + 1
}
return(sum_1)
}
###Here is the deck of 13 cards with their actual value in BlackJack
deck <- c(1,2,3,4,5,6,7,8,9,10,10,10,10)
### This is where I simulate the game 10,000 games of blackjack for the dealer.
###There are 6 possible outcomes for the dealers - getting a hard 17, 18,19, 20, 21 or getting burst.
###We will capture all probabilities in "matrix" which has 13 rows for each card in deck and 6+1 columns for outcomes
matrix <- matrix(0,13,7)
matrix[,1] <- deck
for(j in 1:13){
initial_card <- deck[j]
dealers_hand <- initial_card
sum_vector <- NULL
for (i in 1:10000){
dealers_hand_1 <- dealers_hand
second_card <- sample(deck,1)
dealers_hand_1 <- c(dealers_hand_1,second_card)
inital_sum <- find_sum(dealers_hand_1)
while(inital_sum < 17 | (inital_sum == 17 & inital_sum > sum(dealers_hand_1))) {
dealers_hand_1 <- card_draw(dealers_hand_1)
inital_sum <- find_sum(dealers_hand_1)
}
if(inital_sum > 21) {inital_sum = 0}
sum_vector <- c(sum_vector,inital_sum)
}
matrix[j,2:7] <- table(sum_vector)/10000
}
data <- as.data.frame(matrix)
colnames(data) <- c("Card","0","17","18","19","20","21")
data[,1] <- c("A","2","3","4","5","6","7","8","9","10","J","Q","K")
########Simulation ends here
So what did I find?
Here is the probability distribution given for the first card of the dealer.
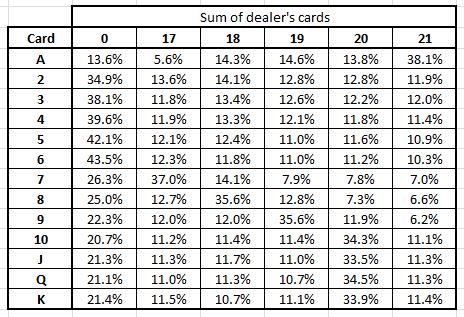
The probability of the dealer getting burst is 39.6%, which will be player’s probability of winning. This means you will loose 60% of times – Is that a good strategy? We can’t answer that question until unless I know what is the probability of winning if I take one more card and either increase or burst my score.
Insight 1 – Probability of the dealer getting burst given his/her first card (say is 4) can be found from the table above (39.6% in this case).
Simulation 2
Now we need to bring in player’s cards as well and find what is the probability of winning if the player has a “14” in hand. With this additional information, we can make refinement to the probability of winning given our 2 cards and dealers 1 card.
###Define the set for player's first 2+ sure card sum. It can be between 12-21. If the sum was less than 12, player will continuously take more cards till he is in this range.
initial_pair <- 12:21
###Define player win probability and tie probability matrix
player_win_matrix1 <- matrix(0,10,13)
player_win_matrix1[,1] <- initial_pair
tie_matrix1 <- matrix(0,10,13)
tie_matrix1[,1] <- initial_pair
###We assume here that player does not draw any additional cards
###Here is the simulation of 5000 games for each possible player final score and dealer's first card
for(i in 1:13){
for(j in 1:10){
initial_card <- initial_pair[j]
players_hand <- initial_card
result_vector <- NULL
player_hand_length <- 2
player_wins <- 0
ties <- 0
dealer_wins <- 0
###Player does not Draws a card!
for (x in 1:5000){
dealer_card <- deck[i]
dealers_hand_1 <- dealer_card
player_sum <- find_sum(players_hand)
dealer_sum <- find_sum(dealers_hand_1)
while(dealer_sum < 17 | (dealer_sum == 17 & dealer_sum > sum(dealers_hand_1))) {
dealers_hand_1 <- card_draw(dealers_hand_1)
dealer_sum <- find_sum(dealers_hand_1)
}
if(dealer_sum > 21) {dealer_sum = 0}
if (dealer_sum == 21 & length(dealers_hand_1) == 2) {dealer_sum = 22}
if (player_sum == 21 & player_hand_length == 2) {player_sum= 22}
if(dealer_sum > player_sum) {dealer_wins <- dealer_wins + 1} else {
if (dealer_sum == player_sum) {ties <- ties + 1} else {player_wins <- player_wins + 1}}
}
player_win_rate <- player_wins/length(result_vector)
tie_rate <- ties/length(result_vector)
player_win_matrix1[j,i] <- player_win_rate
tie_matrix1[j,i] <- tie_rate
}
}

The reason the row 21 has a lot of 100% is that with just 2 cards, 21 is a black jack. And if the dealer does not have the same, the Player is definite to win. The probability of winning for the player sum 12-16 should ideally be equal to the probability of dealer going burst. As this is the only way Player is going to win if he/she chooses to stay. Dealer will have to open a new card if it has a sum between 12-16. This is actually the case which validates that our two simulations are consistent. To decide whether it is worth opening another card, calls into question what will be the probability to win if player decides to take another card.
Insight 2 – If your sum is more than 17 and dealer gets a card 2-6, odds of winning is in your favor. This is even without including Ties.
Simulation 3
###In this simulation the only change from simulation 2 is that, player will pick one additional card.
player_win_matrix1_a_draw <- matrix(0,10,13)
player_win_matrix1_a_draw[,1] <- initial_pair
tie_matrix1_a_draw <- matrix(0,10,13)
tie_matrix1_a_draw[,1] <- initial_pair
for(i in 1:13){
for(j in 1:10){
result_vector <- NULL
player_hand_length <- 2
player_wins <- 0
ties <- 0
dealer_wins <- 0
###Player Draws a card!
for (x in 1:5000){
initial_card <- initial_pair[j]
players_hand <- initial_card
dealer_card <- deck[i]
dealers_hand_1 <- dealer_card
players_hand <- card_draw(players_hand)
player_hand_length <- 3
player_sum <- find_sum(players_hand)
dealer_sum <- find_sum(dealers_hand_1)
while(dealer_sum < 17 | (dealer_sum == 17 & dealer_sum > sum(dealers_hand_1))) {
dealers_hand_1 <- card_draw(dealers_hand_1)
dealer_sum <- find_sum(dealers_hand_1)
}
if(dealer_sum > 21) {dealer_sum = 0}
if(player_sum > 21) {player_sum = 0}
if (dealer_sum == 21 & length(dealers_hand_1) == 2) {dealer_sum = 22}
if (player_sum == 21 & player_hand_length == 2) {player_sum = 22}
if(dealer_sum > player_sum) {dealer_wins <- dealer_wins + 1} else {
if (dealer_sum == player_sum) { ties <- ties + 1 } else {player_wins <- player_wins + 1}}
result_vector <- c(result_vector,end_result)
}
player_win_rate <- player_wins/length(result_vector)
tie_rate <- ties/length(result_vector)
player_win_matrix1_a_draw[j,i] <- player_win_rate
tie_matrix1_a_draw[j,i] <- tie_rate
print(i)
}
}
To make this analysis simple, let’s say favorable probability is Chances to Win + 50% chances to Tie.
Favorable probability table if you choose to draw a card is as follows.

So what did you learn from here. Is it beneficial to draw a card at 8 + 6 or stay?
Favorable probability without drawing a card at 8 + 6 and dealer has 4 ~ 40%
Favorable probability with drawing a card at 8 + 6 and dealer has 4 ~ 43.5%
Clearly you are better off drawing a new card, which was so counter intuitive.
Here is the difference of %Favorable events for each of the combination that can help you design a strategy.

Cells highlighted in green are where you need to pick a new card. Cells highlighted in pink are all stays. Cells not highlighted are where player can make a random choice, difference in probabilities is indifferent.
Insight 2 – Follow the below grid to take a decision whether to stay(0’s) or “hit me” (1’s).

Simulation 4
player_strategy <- read.csv("strategy_1.csv")
strategy <- function(player_hand,dealer_first_card){
player_sum <- find_sum(player_hand)
player_strat <- player_strategy[player_sum - 11,dealer_first_card + 1]
while(player_strat == 1 & player_sum < 22) {
player_hand <- card_draw(player_hand)
player_sum <- find_sum(player_hand)
player_strat <- player_strategy[player_sum - 11,dealer_first_card + 1]
}
return(player_hand)
}
betting_strategy <- function(last_bet,money_left,last_result){
next_bet <- last_bet
return(next_bet)
}
simulate_games <- function(n_iter,total_cash = 100,bet_size_initial = 10){
player_wins <- 0
ties <- 0
dealer_wins <- 0
bet_size = bet_size_initial
cash_flow <- c(rep(total_cash,n_iter+1) )
for(i in 2:n_iter+1){
last_results <- cash_flow[i-1] - cash_flow[i-2]
if(i == 1){bet_size = bet_size_initial} else {bet_size = betting_strategy(bet_size,cash_flow[i-1],last_results)}
dealers_hand <- NULL
player_hand <- NULL
player_first_card <- sample(deck,1)
dealer_first_card <- sample(deck,1)
player_hand <- player_first_card
dealers_hand <- dealer_first_card
##Player gets second card
player_hand <- card_draw(player_hand)
dealer_sum <- find_sum(dealers_hand)
player_sum <- find_sum(player_hand)
while(player_sum < 12) {player_hand <- card_draw(player_hand)
player_sum <- find_sum(player_hand)}
##player's strategy
player_hand <- strategy(player_hand,dealer_first_card)
player_sum <- find_sum(player_hand)
#Dealer has to abide by rules
while(dealer_sum < 17 | (dealer_sum == 17 & dealer_sum > sum(dealers_hand))) {
dealers_hand <- card_draw(dealers_hand)
dealer_sum <- find_sum(dealers_hand)
}
if(dealer_sum > 21) {dealer_sum = 0}
if(player_sum > 21) {player_sum = -1}
if (dealer_sum == 21 & length(dealers_hand) == 2) {dealer_sum = 22}
if (player_sum == 21 & length(player_hand) == 2) {player_sum = 22}
if(dealer_sum > player_sum) {dealer_wins <- dealer_wins + 1
cash_flow[i] <- cash_flow[i-1] - bet_size} else {
if (dealer_sum == player_sum) { ties <- ties + 1
cash_flow[i] <- cash_flow[i-1]} else {player_wins <- player_wins + 1
cash_flow[i] <- cash_flow[i-1] + bet_size
}}
}
player_win_rate <- player_wins/n_iter
tie_rate <- ties/n_iter
player_loose_rate <- 1- (player_win_rate + tie_rate)
final_metrics <- as.data.frame(matrix(0,1,3))
colnames(final_metrics) <- c("Win Rate","TIE Rate","Loose Rate")
final_metrics[1,] <- c(player_win_rate,tie_rate,player_loose_rate)
return_object <- list(final_metrics,cash_flow,cash_flow[i])
return(return_object)
}
a <- simulate_games(n_iter = 100000,total_cash = 10000, bet_size_initial= 20)
Assuming the above simulation, here are the rates of win/loss/ties:
Win Rate = 41.4%
Tie Rate = 9.5%
Loss Rate = 49.1%
SHOCKER!!! Our win rate is far lower than the loss rate of the game. It would have been much better if we just tossed a coin. The biggest difference is that the dealer wins if both the player and the dealer gets burst. If you remove that single condition, here are the win/loss rate.
Win Rate = 41.4%
Tie Rate = 17.1%
Loss Rate = 41.5%
As you can see, both dealer and player burst in about 8% of the games. By just changing this small thing, Casino’s make sure that we loose much more frequently than the house do.
Insight 3 – Even with the best strategy, a player wins 41% times as against dealer who wins 49% times. The difference is driven by the tie breaker when both player and dealer goes burst.
This is consistent with our burst table, which shows that probability of the dealer getting burst is 28.4%. Hence, both the player and the dealer getting burst will be 28.4% * 28.4% ~ 8%.
Deep dive into betting strategy
Now we know what is the right gaming strategy, however, even the best gaming strategy can lead you to about 41% wins and 9% ties, leaving you to a big proportion of losses. Is there a betting strategy that can come to rescue us from this puzzle?
The probability of winning in blackjack is known now. To find the best betting strategy, let’s simplify the problem. We know that the strategy that works in a coin toss event will also work in black jack. However, coin toss event is significantly less computationally intensive.
Simulation 5
### We toss a coin, if it lands as per your call, you win 2X of the money you bet; Pocket is the initial amount you got for betting
### Min_bet is the minimum bet in this game; last victory is 1 if you won the last game.
simulation <- function(pocket = 100, min_bet = 1,games = 500){
win = 0;bet <- min_bet; last_victory <- 1;money_flow <- NULL
for (i in 1:games){
bet <- betting_strategy(bet,last_victory,min_bet,pocket)
if(sample(1:10,1) > 5) {win = win + 1
last_victory = 1
pocket <- pocket + bet} else {last_victory = -1
pocket <- pocket - bet}
money_flow <- c(money_flow,pocket)
}
return(c(pocket,win))
}
#Here is the first betting strategy- we bet only minimum bet untill unless player becomes bankrupt
betting_strategy <- function(last_bet,last_result,min_bet,left_bal){
next_bet <- min_bet
if(left_bal <= 0) {next_bet <- 0}
return(next_bet)
}
#Run a simple simulation
simple_bet <- matrix(0,1000,2)
for(i in 1:1000){
simple_bet[i,] <- simulation(pocket = 100,min_bet = 20,games = 100)
}
Avg. number of games won = 50
Avg. money you walk out of Casino = $99.74 ~ $100
Max money won = $780
%times person becomes bankrupt = 63.1%
Did any of the above 4 metrics shock you? What got me to thinking was that even though the average value of anyone leaving the casino is same as what one starts with, the percentage times someone becomes bankrupt is much higher than 50%. Also, if you increase the number of games, the percentage times someone becomes bankrupt increases. Why is that?
The reason is that we have a lower bound at $0 which is bankruptcy, but we don’t have an upper bound. On your lucky days, you can win as much as you can possibly win, and Casino will never stop you saying that Casino is now bankrupt. So in this biased game between you and Casino, for a non-rigged game, both you and Casino has the expected value of no gain no loss. But you have a lower bound and Casino has no lower bound. Simply put, let’s assume that you start with $100. If you win you can reach as high as $1000 or even $10k. But the expected value of your final amount is still $100 as the game was even. So, to pull the expected value down, a high number of people like you have to become bankrupt. Let us validate this theory through a simuation using the previously defined functions.
Simulation 6
final <- matrix(0,10,5)
final[,1] <- 1:10
for(j in 1:10){
simple_bet <- matrix(0,500,2)
for(i in 1:500){
simple_bet[i,] <- simulation(pocket = 100,min_bet = 20,games = j*50)
}
final[j,2] <- nrow(simple_bet[simple_bet[,1] == 0,])/nrow(simple_bet)
final[j,3] <- mean(simple_bet[,1])
final[j,4] <- max(simple_bet[,1])
final[j,5] <- mean(simple_bet[,2])/j*50
}
final <- as.data.frame(final)
colnames(final) <- c("#Games","Bankruptcy Rate","Mean earning", "Max earning","% wins")

In Mathematical style – Hence Proved!
Clearly the bankruptcy rate and maximum earning seem correlation. What it means is that the more games you play, your probability of becoming bankrupt and becoming a millionaire both increases simultaneously. So, if it is not your super duper lucky day, you will end up loosing everything. Imagine 10 people P1, P2, P3, P4 ….P10.
P10 is most lucky, P9 is second in line….P1 is the most unlucky.
If all of them start with $100, the first one becoming bankrupt will be P1, and his $100 is divided among the other 9. Next in line of bankruptcy is P2 and so on. So, you might think P3 is on his lucky day, but if he/she plays enough number of games after P4 is gone, he is now fueling the earning of P2 and P1. In no time, P1 and P2 would rob P3. Obviously P2 is next and finally P1 will leave the casino with $1000 in his/her pocket. Casino is just a medium to redistribute wealth if the games are fair and not rigged, which we have already concluded is not the case. If all P1-P10 are playing black jack, I won’t be surprised if all of them loose bankrupt as dealer has higher odds of winning a game.
Insight 4 – The more games you play, the chances of your bankruptcy and maximum amount you can win, both increases for a fair game (which itself is a myth).
Is there a way to control for this bankruptcy in a non-bias game? Fortunately YES!
What if we make the game fair. The lowest you can reach is a loss of $100. Let us now fix the highest profit you reach is also $100, and then you stop no matter what. Let’s try to simulate this.
Simulation 7
##Capping the total winning to 100%
betting_strategy <- function(last_bet,last_result,min_bet,left_bal){
next_bet <- min_bet
if(left_bal <= 0 | left_bal >= 200) {next_bet <- 0}
return(next_bet)
}
simple_bet <- matrix(0,1000,2)
for(i in 1:1000){
simple_bet[i,] <- simulation(pocket = 100,min_bet = 20,games = 100)
}
Avg. number of games won = 50
Avg. money you walk out of Casino = $99.34 ~ $100
Max money won = $200
%times person becomes bankrupt = 47.5%
BINGO! % times reaching $0 is 50% and other 50% reach $200. Now this looks fair! Let us run the same simulation we ran with the earlier strategy.

Again mathematician style – Hence Proved! The Bankruptcy rate clearly fluctuates around 50%. You can decrease it even further if you cap your earning at a lower % than 100%. But sadly, no one can cap their winning when they are in Casino. And not stopping at 100% makes them more likely to become bankrupt later.
Insight 5 – The only way to win in a Casino is to decide the limit of winning. On your lucky day, you will actually win that limit. If you do otherwise, you will be bankrupt even in your most lucky day.
Enough of this monologue, let’s try some hands-on exercise
Here are a few exercise you can try solving and reply back in the comment section.
Exercise 1 (Level : Low) – If you set your higher limit of earning as 50% instead of 100%, at what % will your bankruptcy rate reach a stagnation?
Exercise 2 (Level : High) – Martingale is a famous betting strategy. The rule is simple, whenever you loose, you make the bet twice of the last bet. Once you win, you come back to the original minimum bet. For instance, your start with $1. You win 3 games and then you loose 3 games and finally you win 1 game. So your series of wins will be
$1 + $1 + $1 + (- $1 - $2 - $4 + $8) = $1 + $1 + $1 + $1 = $4
Basically what happens is that if you break any loosing streak, you recover all the money you have invested with profit same a minimum bet. For such a betting strategy, find:
a. If the expected value of winning changes?
b. Does probability of winning changes at the end of a series of game? You can give the results as a function of number of games/minimum bet/total initial money in your pocket.
c. Is this strategy any better than our constant value strategy (without any upper bound)? Talk about bankruptcy rate, expect value at the end of series, probability to win more games, highest earning potential.
d. Does the strategy makes sense if you play a high number of matches or low number of matches for say – Minimum bet of $1 and Total initial money in pocket $100. High number of matches can be as high as 500, low number of matches can be as low as 10.
Exercise 3 (Level – Medium) – For the Martingale strategy, does it make sense to put a cap on earning at 100% to decrease the chances of bankruptcy? Is this strategy any better than our constant value strategy (with 100% upper bound with constant betting)? Talk about bankruptcy rate, expect value at the end of series, probability to win more games, highest earning potential.
End Notes
Casinos are the best place to apply concepts of mathematics and the worst place to test these concepts. As most of the games are rigged, you will only have fair chances to win while playing against other players, in games like Poker. If there was one thing you want to take away from this article before entering a Casino, that will be always fix the upper bound to %earning. You might think that this is against your winning streak, however, this is the only way to play a level game with Casino.
I hope you enjoyed reading this articl. If you use these strategies next time you visit a Casino I bet you will find them extremely helpful. If you have any doubts feel free to post them below.
Now, I am sure you are excited enough to solve the three examples referred in this article. Make sure you share your answers with us in the comment section.
Learn, compete, hack and get hired!






My brother applied the same and did win :)
Uumm. The odds in a casino are not in line with the odds of winning.. Your number will come 1/37, however you will be paid 1 to 35 = 36 when it comes in. So you lose 1 bet even when you win, and that is the casino's edge.
Correctly pointed out. Or we could just go random as well in the game and yet come out even every time.
Very helpful & well written artical. I enjoyed It. Thank you.