Overview
- An introduction to link prediction, how it works, and where you can use it in the real-world
- Learn about the importance of Link Prediction on social media
- Build your first Link Prediction model for a Facebook use case using Python
Introduction
Have you ever wondered who your next Facebook connection might be? Curious who the next request might come from?
What if I told you there was a way to predict this?
I love brainstorming and coming up with these problem statements when I’m browsing through my Facebook account. It’s one of the perks of having a data scientist’s mindset!
Most social media platforms, including Facebook, can be structured as graphs. The registered users are interconnected in a universe of networks. And to work on these networks and graphs, we need a different set of approaches, tools, and algorithms (instead of traditional machine learning methods).
So in this article, we will solve a social network problem with the help of graphs and machine learning. We will first understand the core concepts and components of link prediction before taking up a Facebook case study and implementing it in Python!
I recommend going through the below articles to get a hang of what graphs are and how they work:
- Introduction to Graph Theory and its Applications using Python
- Knowledge Graph – A Powerful Data Science Technique to Mine Information from Text
Table of Contents
- An Overview of Social Network Analytics
- A Primer on Link Prediction
- Strategy to Solve a Link Prediction Problem
- Case Study: Predict Future Connections between Facebook Pages
- Understanding the Data
- Dataset Preparation Model Building
- Feature Extraction
- Model Building: Link Prediction Model
An Overview of Social Network Analytics
Let’s define a social network first before we dive into the concept of link prediction.
A social network is essentially a representation of the relationships between social entities, such as people, organizations, governments, political parties, etc.
The interactions among these entities generate unimaginable amounts of data in the form of posts, chat messages, tweets, likes, comments, shares, etc. This opens up a window of opportunities and use cases we can work on.
That brings us to Social Network Analytics (SNA). We can define it as a combination of several activities that are performed on social media. These activities include data collection from online social media sites and using that data to make business decisions.
The benefits of social network analytics can be highly rewarding. Here are a few key benefits:
- Helps you understand your audience better
- Used for customer segmentation
- Used to design Recommendation Systems
- Detect fake news, among other things
A Primer on Link Prediction
Link prediction is one of the most important research topics in the field of graphs and networks. The objective of link prediction is to identify pairs of nodes that will either form a link or not in the future.
Link prediction has a ton of use in real-world applications. Here are some of the important use cases of link prediction:
- Predict which customers are likely to buy what products on online marketplaces like Amazon. It can help in making better product recommendations
- Suggest interactions or collaborations between employees in an organization
- Extract vital insights from terrorist networks
In this article, we will explore a slightly different use case of link prediction – predicting links in an online social network!
Strategy to Solve a Link Prediction Problem
If we can somehow represent a graph in the form of a structured dataset having a set of features, then maybe we can use machine learning to predict the formation of links between the unconnected node-pairs of the graph.tcou
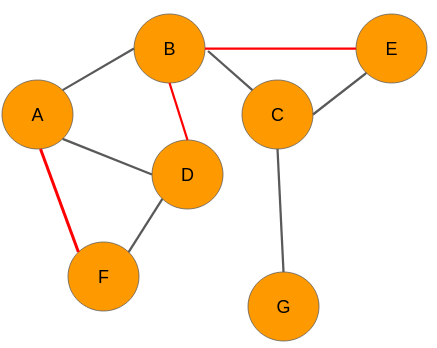
Let’s take a dummy graph to understand this idea. Given below is a 7 node graph and the unconnected node-pairs are AF, BD, BE, BG, and EG:
Graph at time t
Now, let’s say we analyze the data and came up with the below graph. A few new connections have been formed (links in red):
Graph at time t+n
We need to have a set of predictor variables and a target variable to build any kind of machine learning model, right? So where are these variables? Well, we can get it from the graph itself! Let’s see how it is done.
Our objective is to predict whether there would be a link between any 2 unconnected nodes. From the network at time t, we can extract the following node pairs which have no links between them:
- A-F
- B-D
- B-E
- B-G
- E-G
Please note that, for convenience, I have considered only those nodes that are a couple of links apart.
The next step for us is to create features for each and every pair of nodes. The good news is that there are several techniques to extract features from the nodes in a network. Let’s say we use one of those techniques and build features for each of these pairs. However, we still don’t know what the target variable is. Nothing to worry about – we can easily obtain that as well.
Look at the graph at time t+n. We can see that there are three new links in the network for the pairs A-F, B-D, and BE respectively. Therefore, we will assign each one of them a value of 1. The node pairs B-G and E-G will be assigned 0 because there are still no links between the nodes.
Hence, the data will look like this:
Now that we have the target variable, we can build a machine learning model using this data to perform link prediction.
So, this is how we need to use social graphs at two different instances of time to extract the target variable, i.e., the presence of a link between a node pair. Keep in mind, however, that in real-world scenarios, we will have data of the present time only.
Extract data from a Graph for Building your Model
In the section above, we were able to get labels for the target variable because we had access to the graph at time t+n. However, in real-world scenarios, we would have just one graph dataset in hand. That’s it!
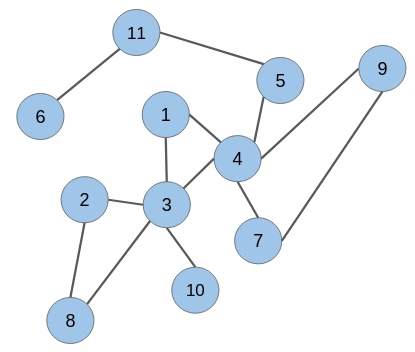
Let’s say we have the below graph of a social network where the nodes are the users and the edges represent some kind of relationship:
The candidate node pairs, which may form a link at a future time, are (1 & 2), (2 & 4), (5 & 6), (8 & 10), and so on. We have to build a model that will predict if there would be a link between these node pairs or not. This is what link prediction is all about!
However, to build a link prediction model, we need to prepare a training dataset out of this graph. It can be done using a simple trick.
Picture this – how would this graph have looked like at some point in the past? There would be fewer edges between the nodes because connections in a social network are built gradually over time.
Hence, keeping this in mind, we can randomly hide some of the edges from the given graph and then follow the same technique as explained in the previous section to create the training dataset.
Strike Off Links from the Graph
While removing links or edges, we should avoid removing any edge that may produce an isolated node (node without any edge) or an isolated network. Let’s take off some of the edges from our network:
As you can see, the edges in the node pairs (1 & 4), (7 & 9), and (3 & 8) have been removed.
Add labels to extracted data
Next, we would need to create features for all the unconnected node pairs including the ones for which we have omitted the edges. The removed edges will be labeled as ‘1’ and the unconnected node pairs as ‘0’:
| Features | Link (Target Variable) |
| Features of node pair 1 – 2 | 0 |
| Features of node pair 1 – 5 | 0 |
| Features of node pair 1 – 7 | 0 |
| Features of node pair 1 – 8 | 0 |
| Features of node pair 1 – 9 | 0 |
| Features of node pair 1 – 10 | 0 |
| Features of node pair 2 – 4 | 0 |
| Features of node pair 2 – 10 | 0 |
| Features of node pair 3 – 5 | 0 |
| Features of node pair 3 – 7 | 0 |
| Features of node pair 3 – 9 | 0 |
| Features of node pair 4 – 8 | 0 |
| Features of node pair 4 – 10 | 0 |
| Features of node pair 4 – 11 | 0 |
| Features of node pair 5 – 6 | 0 |
| Features of node pair 5 – 7 | 0 |
| Features of node pair 5 – 9 | 0 |
| Features of node pair 8 – 10 | 0 |
| Features of node pair 1 – 4 | 1 |
| Features of node pair 3 – 8 | 1 |
| Features of node pair 7 – 9 | 1 |
It turns out that the target variable is highly imbalanced. This is what you will encounter in real-world graphs as well. The number of unconnected node pairs would be huge.
Let’s take up a case study and solve the problem of link prediction using Python.
Case Study: Predict Future Connections between Facebook Pages
This is where we’ll apply all of the above into an awesome real-world scenario.
We will work with a graph dataset in which the nodes are Facebook pages of popular food joints and well-renowned chefs from across the globe. If any two pages (nodes) like each other, then there is an edge (link) between them.
You can download the dataset from here.
Objective: Build a link prediction model to predict future links (mutual likes) between unconnected nodes (Facebook pages).
Let’s fire up our Jupyter Notebook (or Colab)!
Understanding the Data
We will first import all the necessary libraries and modules:
Let’s load the Facebook pages as the nodes and mutual likes between the pages as the edges:
Output: (620, 2102)
We have 620 nodes and 2,102 links. Let’s now create a dataframe of all the nodes. Every row of this dataframe represents a link formed by the nodes in the columns ‘node_1’ and ‘node_2’, respectively:
fb_df.head()
The nodes ‘276’, ’58’, ‘132’, ‘603’, and ‘398’ form links with the node ‘0’. We can easily represent this arrangement of Facebook pages in the form of a graph:
Wow, that looks quite something. This is what we are going to deal with – a wire mesh of Facebook pages (blue dots). The black lines are the links or edges connecting all the nodes to each other.
Dataset Preparation for Model Building
We need to prepare the dataset from an undirected graph. This dataset will have features of node pairs and the target variable would be binary in nature, indicating the presence of links (or not).
Retrieve Unconnected Node Pairs – Negative Samples
We have already understood that to solve a link prediction problem, we have to prepare a dataset from the given graph. A major part of this dataset is the negative samples or the unconnected node pairs. In this section, I will show you how we can extract the unconnected node pairs from a graph.
First, we will create an adjacency matrix to find which pairs of nodes are not connected.
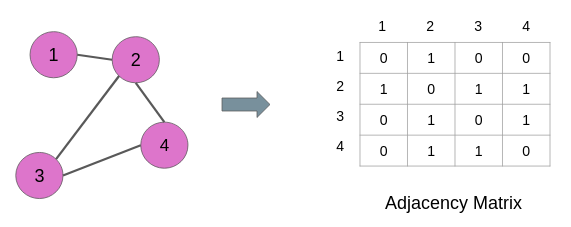
For example, the adjacency of the graph below is a square matrix in which the rows and columns are represented by the nodes of the graph:
The links are denoted by the values in the matrix. 1 means there is a link between the node pair and 0 means there is a link between the node pair. For instance, nodes 1 and 3 have 0 at their cross-junction in the matrix and these nodes also have no edge in the graph above.
We will use this property of the adjacency matrix to find all the unconnected node pairs from the original graph G:
Let’s check out the shape of the adjacency matrix:
adj_G.shape
Output: (620, 620)
As you can see, it is a square matrix. Now, we will traverse the adjacency matrix to find the positions of the zeros. Please note that we don’t have to go through the entire matrix. The values in the matrix are the same above and below the diagonal, as you can see below:
We can either search through the values above the diagonal (green part) or the values below (red part). Let’s search the diagonal values for zero:
Here’s how many unconnected node pairs we have in our dataset:
len(all_unconnected_pairs)
Output: 19,018
We have 19,018 unconnected pairs. These node pairs will act as negative samples during the training of the link prediction model. Let’s keep these pairs in a dataframe:
Remove Links from Connected Node Pairs – Positive Samples
As we discussed above, we will randomly drop some of the edges from the graph. However, randomly removing edges may result in cutting off loosely connected nodes and fragments of the graph. This is something that we have to take care of. We have to make sure that in the process of dropping edges, all the nodes of the graph should remain connected.
In the code block below, we will first check if dropping a node pair results in the splitting of the graph (number_connected_components > 1) or reduction in the number of nodes. If both things do not happen, then we drop that node pair and repeat the same process with the next node pair.
Eventually, we will get a list of node pairs that can be dropped from the graph and all the nodes would still remain intact:
len(omissible_links_index)
Output: 1483
We have over 1400 links that we can drop from the graph. These dropped edges will act as positive training examples during the link prediction model training.
Data for Model Training
Next, we will append these removable edges to the dataframe of unconnected node pairs. Since these new edges are positive samples, they will have a target value of ‘1’:
Let’s check the distribution of values of the target variable:
data['link'].value_counts()
0 19018
1 1483
It turns out that this is highly imbalanced data. The ratio of link vs no link is just close to 8%. In the next section, we will extract features for all these node pairs.
Feature Extraction
We will use the node2vec algorithm to extract node features from the graph after dropping the links. So, let’s first create a new graph after dropping the removable links:
Next, we will install the node2vec library. It is quite similar to the DeepWalk algorithm. However, it involves biased random walks. To know more about node2vec, you should definitely check out this paper node2vec: Scalable Feature Learning for Networks.
For the time being, just keep in mind node2vec is used for vector representation of nodes of a graph. Let’s install it:
!pip install node2vec
It might take a while to install on your local machine (it’s quite fast if you’re using Colab).
Now, we will train the node2vec model on our graph (G_data):
Next, we will apply the trained node2vec model on each and every node pair in the dataframe ‘data’. To compute the features of a pair or an edge, we will add up the features of the nodes in that pair:
x = [(n2w_model[str(i)]+n2w_model[str(j)]) for i,j in zip(data['node_1'], data['node_2'])]
Building our Link Prediction Model
To validate the performance of our model, we should split our data into two parts – one for training the model and the other to test the model’s performance:
Let’s fit a logistic regression model first:
We will now make predictions on the test set:
predictions = lr.predict_proba(xtest)
We will use the AUC-ROC score to check our model’s performance. To learn more about this evaluation metric, you may check out this article: Important Model Evaluation Metrics for Machine Learning.
roc_auc_score(ytest, predictions[:,1])
Output: 0.7817
The training stopped after the 208th iteration because we applied the early stopping criteria. Most importantly, the model got an impressive 0.9273 AUC score on the test set. I encourage you to take a look at the lightGBM documentation to learn more about the different parameters.
End Notes
There is enormous potential in graphs. We can harness this to solve a large number of real-world problems, of which link prediction is one.
In this article, we have showcased how a link prediction problem can be tackled using machine learning, and what are the limitations and important aspects that we have to keep in mind while solving such a problem.
Please feel free to ask any questions or leave your feedback in the comments section below. Keep exploring!












Why isn't the precision and recall presented on such an imbalanced dataset. :(
Thank you so much for your great post. I have two questions: 1. I don't understand why there are only 19018 unconnected pairs. The size of adjacency matrix G is (620,620). So, there are 620X620=384400 elements. We only search the values above or below the diagonal for zero. In total, we will search (384400-620)/2=191890 elements for zero. Because we have 2102 connected pairs, so we should have 191890-2102=189788 unconnected pairs. 2. When you did feature extraction, why did train node2vec using the graph after dropping the links (the nodes connected before) only?
Answer for 2: IF I got it right then it is due to the fact that we can verify if an only iff there was a link between 2 nodes. For example how will we test if our model predicted correctly? If we know that at t-n there was a link and we removed the value at t and again predicted at t+n that A and B will form a link so we can check whether our original data had links between A and B.
The shortest path condition allows only those nodes to be considered which have a shortest path value of <= 2. This I guess filters out a large number of unconnected pairs because we do not need all unconnected pairs for training the model. Negative samples serve to build more robust models.
Thanks for sharing this article with us. i enjoyed reading it. it is informational. Thank you.