This article was published as a part of the Data Science Blogathon.
Introduction
In this article, you will find the different ways to calculate vector norms or magnitudes, known as the Vector Norm. It is defined as the length or magnitude of the vector. This concept of norms is important in Machine Learning and Deep Learning. The norm is generally used to evaluate the error of the model.
For instance, it is used to calculate the error between the output of a Neural network and what is expected(the actual value or label) or can be used in defining a regularization term which includes the magnitude of the weights, to encourage small weights. It is a function that maps a vector to a positive value(which means the norm is always a positive value). Different functions can be used and we will see few examples. Norms are any functions that are characterized by the following properties:
– Vector Norms are non-negative values. If you think of the norms as a length, you easily see why they can’t be negative.
– Vector Norms are 0 if and only if the vector is itself a zero vector.
– Norms follow the triangular inequality(The norm of the sum of some vectors is less than or equal to the sum of the norms of these vectors).
– When a vector is stretched, the norm is multiplied by the stretching factor.
Vector Norm
The length of a vector is a nonnegative number that describes the extent of the vector in space, and is sometimes referred to as the vector’s magnitude or the norm.
Notations are used to represent the vector norm in broader calculations and the type of vector norm calculation almost always has its own unique notation.
We will take a look at a few common vector norm calculations used in machine learning.
1. Vector L1 Norm: The length of a vector can be calculated using the L1 norm.
– The notation for the L1 norm of a vector is ||v||1 and this type of norm is sometimes also referred to as Manhattan Norm(since this uses Manhattan distance ).
– The L1 norm is calculated as the sum of the absolute vector values(which means add the absolute value of vector components in different directions) and the absolute value of a scalar is representing using the notation as |b1|. So, this norm is a calculation of the Manhattan distance from the origin to the vector space.
||v||1= |b1| + |b2| +|b3|
where bi is the components of a given vector in different directions.
– In Machine learning, we usually use L1 norm when the sparsity of vector matters i.e when the essential factor is the no-zero elements of a matrix(because this norm simply targets the non-zero elements by adding them up).
– The L1 norm of a vector can be calculated using the norm( ) function present in the Linear Algebra module inside the Numpy library.
import numpy as np # import necessary dependency with alias as np
from numpy.linalg import norm
arr=np.array([1,3,5]) #formation of an array using numpy library
l1=norm(arr,1) # here 1 represents the order of the norm to be calculated
print(l1)
2. Vector L2 Norm: The length of a vector can be calculated using the L2 norm.
– The notation for the L2 norm of a vector is ||v||2 and this type of norm is also known as Euclidean Norm(since this uses Euclidean distance ).
– The L2 norm is calculated as the square root of the sum of the squared vector values. So, this norm finds the distance of the vector coordinate from the origin of the vector space.
||v||2= sqrt [ (b1)2 + (b2)2 + (b3)2 ]
– The L2 norm of a vector can be calculated using the norm( ) function with default parameters(means default order in the norm function is 2).
– This type of norm is most commonly used in Machine Learning(due to being a differentiable function, which is crucial for optimization purposes).
import numpy as np # import necessary dependency with alias as np
from numpy.linalg import norm
arr=np.array([1,3,5]) #formation of an array using numpy library
l2 =norm(arr,2) # here 2 represents the order of the norm to be calculated
print(l2)
3. Vector Max Norm: The length of a vector can be calculated using the max norm.
– This norm is referred to as Linf and also can be represented with the infinity symbol. The notation for max norm is ||v||inf .
– The max norm is calculated as returning the max value of the vector.
||v||inf = max( |b1| , |b2| , |b3| )
– The max norm of a vector can be calculated using the norm( ) function along with set the parameter as inf which is a order for norm).
import numpy as np # import necessary dependency with alias as np
from numpy.linalg import norm
arr=np.array([1,3,5]) #formation of an array using numpy library
maxnorm =norm(arr,inf) # here inf represents the order of the norm
print(maxnorm)
Note:
The general form of vector norms (also known as p-norm)
Norm of a matrix
– For calculating the norm of a matrix, we have the unusual definition of Frobenius norm which is very similar to L2 vector norm.
– The Frobenius norm of a matrix is defined as the square root of the sum of the squares of the elements of the matrix.
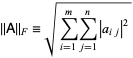
– The Frobenius norm can also be considered as a vector norm.
where AH is the conjugate transpose of the matrix A.
End Notes
In this article, you learned what the norms are and how to implement them, which are crucial when we using any Machine or Deep learning algorithms. Specifically, you learned about L1, L2, and Link norms with the help of this article. Make sure to play with the Python codes which we are using in this article and try the implementation yourself from scratch. I assure you it will help you to gain a better understanding. I hope you find it useful.
Please don’t forget to share your thoughts with me.
Do you have any questions?
Ask your questions in the comment below and I will do my best to answer.
About the Author
Chirag Goyal
Currently, I pursuing my Bachelor of Technology (B.Tech) in Computer Science and Engineering from the Indian Institute of Technology Jodhpur(IITJ). I am very enthusiastic about Machine learning, Deep Learning, and Artificial Intelligence. If you want to connect with me here is the link to my Linkedin profile.
http://linkedin.com/in/chirag-goyal-3419671a0
Also, here is the link to my other blogs which might help you to learn some different concepts in the field of Machine Learning and Artificial Intelligence.
Multicollinearity in Data Science
Standardized and unstandardized coefficient of regression
The media shown in this article are not owned by Analytics Vidhya and is used at the Author’s discretion.
I am a B.Tech. student (Computer Science major) currently in the pre-final year of my undergrad. My interest lies in the field of Data Science and Machine Learning. I have been pursuing this interest and am eager to work more in these directions. I feel proud to share that I am one of the best students in my class who has a desire to learn many new things in my field.
thanks for such a nice article! :)