Interview Prep
Career
GenAI
Prompt Engg
ChatGPT
LLM
Langchain
RAG
AI Agents
Machine Learning
Deep Learning
GenAI Tools
LLMOps
Python
NLP
SQL
AIML Projects

Reading list

Machine Learning Basics for a Newbie
6 Steps of Machine learning Lifecycle Introduction to Predictive Modeling
Introduction to Exploratory Data Analysis & Data Insights Descriptive Statistics Inferential Statistics How to Understand Population Distributions?
Reading Data Files into Python Different Variable Datatypes
Probability for Data Science Basic Concepts of Probability Axioms of Probability Conditional Probability
Central Tendencies for Continuous Variables Spread of Data KDE plots for Continuous Variable Overview of Distribution for Continuous variables Normal Distribution Skewed Distribution Skeweness and Kurtosis Distribution for Continuous Variable
Central Tendencies for Categorical Variables Understanding Discrete Distributions Performing EDA on Categorical Variables
Dealing with Missing Values Understanding Outliers Identifying Outliers in Data Outlier Detection in Python Outliers Detection Using IQR, Z-score, LOF and DBSCAN
Sample and Population Central Limit Theorem Confidence Interval and Margin of Error
Bivariate Analysis Introduction
Covariance Pearson Correlation Spearman's Correlation & Kendall's Tau Correlation versus Causation Tabular and Graphical methods for Bivariate Analysis Performing Bivariate Analysis on Continuous-Continuous Variables
Tabular and Graphical methods for Continuous-Categorical Variables Introduction to Hypothesis Testing P-value Two sample Z-test T-test T-test vs Z-test Performing Bivariate Analysis on Continuous-Catagorical variables
Chi-Squares Test Bivariate Analysis on Categorical Categorical Variables
Multivariate Analysis A Comprehensive Guide to Data Exploration The Data Science behind IPL
Supervised Learning vs Unsupervised Learning Reinforcement Learning Generative and Descriminative Models Parametric and Non Parametric model
Machine Learning Pipeline Preparing Dataset Build a Benchmark Model: Regression Build a Benchmark Model: Classification
Evaluation Metrics for Machine Learning Everyone should know Confusion Matrix Accuracy Precision and Recall AUC-ROC Log Loss R2 and Adjusted R2
Dealing with Missing Values Replacing Missing Values Imputing Missing Values in Data Working with Categorical Variables Working with Outliers Preprocessing Data for Model Building
Understanding Cost Function Understanding Gradient Descent Math Behind Gradient Descent Assumptions of Linear Regression Implement Linear Regression from Scratch Train Linear Regression in Python Implementing Linear Regression in R Diagnosing Residual Plots in Linear Regression Models Generalized Linear Models Introduction to Logistic Regression Odds Ratio Implementing Logistic Regression from Scratch Introduction to Scikit-learn in Python Train Logistic Regression in python Multiclass using Logistic Regression How to use Multinomial and Ordinal Logistic Regression in R ? Challenges with Linear Regression Introduction to Regularisation Implementing Regularisation Ridge Regression Lasso Regression
Introduction to K Nearest Neighbours Determining the Right Value of K in KNN Implement KNN from Scratch Implement KNN in Python
Bias Variance Tradeoff Introduction to Overfitting and Underfitting Visualizing Overfitting and Underfitting Selecting the Right Model What is Validation? Hold-Out Validation Understanding K Fold Cross Validation
Introduction to Feature Selection Feature Selection Algorithms Missing Value Ratio Low Variance Filter High Correlation Filter Backward Feature Elimination Forward Feature Selection Implement Feature Selection in Python Implement Feature Selection in R
Introduction to Decision Tree Purity in Decision Tree Terminologies Related to Decision Tree How to Select Best Split Point in Decision Tree? Chi-Squares Information Gain Reduction in Variance Optimizing Performance of Decision Tree Train Decision Tree using Scikit Learn Pruning of Decision Trees
Introduction to Feature Engineering Feature Transformation Feature Scaling Feature Engineering Frequency Encoding Automated Feature Engineering: Feature Tools
Introduction to Naive Bayes Conditional Probability and Bayes Theorem Introduction to Bayesian Adjustment Rating: The Incredible Concept Behind Online Ratings! Working of Naive Bayes Math behind Naive Bayes Types of Naive Bayes Implementation of Naive Bayes
Understanding how to solve Multiclass and Multilabled Classification Problem Evaluation Metrics: Multi Class Classification
Introduction to Ensemble Techniques Basic Ensemble Techniques Implementing Basic Ensemble Techniques Finding Optimal Weights of Ensemble Learner using Neural Network Why Ensemble Models Work well?
Introduction to Stacking Implementing Stacking Variants of Stacking Implementing Variants of Stacking Introduction to Blending Bootstrap Sampling Introduction to Random Sampling Hyper-parameters of Random Forest Implementing Random Forest Out-of-Bag (OOB) Score in the Random Forest IPL Team Win Prediction Project Using Machine Learning Introduction to Boosting Gradient Boosting Algorithm Math behind GBM Implementing GBM in python Regularized Greedy Forests Extreme Gradient Boosting Implementing XGBM in python Tuning Hyperparameters of XGBoost in Python Implement XGBM in R/H2O Adaptive Boosting Implementing Adaptive Boosing LightGBM Implementing LightGBM in Python Catboost Implementing Catboost in Python
Different Hyperparameter Tuning methods Implementing Different Hyperparameter Tuning methods GridsearchCV RandomizedsearchCV Bayesian Optimization for Hyperparameter Tuning Hyperopt
Understanding SVM Algorithm SVM Kernels In-depth Intuition and Practical Implementation SVM Kernel Tricks Kernels and Hyperparameters in SVM Implementing SVM from Scratch in Python and R
Introduction to Principal Component Analysis Steps to Perform Principal Compound Analysis Computation of Covariance Matrix Finding Eigenvectors and Eigenvalues Implementing PCA in python Visualizing PCA A Brief Introduction to Linear Discriminant Analysis Introduction to Factor Analysis
Introduction to Clustering Applications of Clustering Evaluation Metrics for Clustering Understanding K-Means Implementation of K-Means in Python Implementation of K-Means in R Choosing Right Value for K Profiling Market Segments using K-Means Clustering Hierarchical Clustering Implementation of Hierarchial Clustering DBSCAN Defining Similarity between clusters Build Better and Accurate Clusters with Gaussian Mixture Models
Understand Basics of Recommendation Engine with Case Study
8 Ways to Improve Accuracy of Machine Learning Models
Introduction to Dask Working with CuML
Introduction to Machine Learning Interpretability Framework and Interpretable Models model Agnostic Methods for Interpretability Implementing Interpretable Model Understanding SHAP Out-of-Core ML Introduction to Interpretable Machine Learning Models Model Agnostic Methods for Interpretability Game Theory & Shapley Values
Introduction to Machine Learning Interpretability Framework and Interpretable Models model Agnostic Methods for Interpretability Implementing Interpretable Model Understanding SHAP Out-of-Core ML Introduction to Interpretable Machine Learning Models Model Agnostic Methods for Interpretability Game Theory & Shapley Values
Introduction to AutoML Implementation of MLBox Introduction to PyCaret TPOT Auto-Sklearn EvalML
Pickle and Joblib Introduction to Model Deployment
Deploying Machine Learning Model using Streamlit Deploying ML Models in Docker Deploy Using Streamlit Deploy on Heroku Deploy Using Netlify Introduction to Amazon Sagemaker Setting up Amazon SageMaker Using SageMaker Endpoint to Generate Inference Deploy on Microsoft Azure Cloud Introduction to Flask for Model Deploying ML model using Flask
Model Deployment in Android Model Deployment in Iphone

Bagging- 25 Questions to Test Your Skills on Random Forest Algorithm

Chirag Goyal
Chirag Goyal Last Updated : 19 Jul, 2024
12 min read

This article was published as a part of the Data Science Blogathon

Introduction

Random Forest (Ensemble technique) is a Supervised Machine Learning Algorithm that is constructed with the help of decision trees. This algorithm is heavily used in various industries such as Banking and e-commerce to predict behavior and outcomes.

Therefore it becomes necessary for every aspiring Data Scientist and Machine Learning Engineer to have a good knowledge of the Random Forest Algorithm.

In this article, we will discuss the most important questions on the Random Forest Algorithm which is helpful to get you a clear understanding of the Algorithm, and also for Data Science Interviews, which covers its very fundamental level to complex concepts.

 

Let’s get started,

1. What do you mean by Random Forest Algorithm?

Random forest is an ensemble machine learning technique that averages several decision trees on different parts of the same training set, with the objective of overcoming the overfitting problem of the individual decision trees.

In other words, a random forest algorithm is used for both classification and regression problem statements that operate by constructing a lot of decision trees at training time.

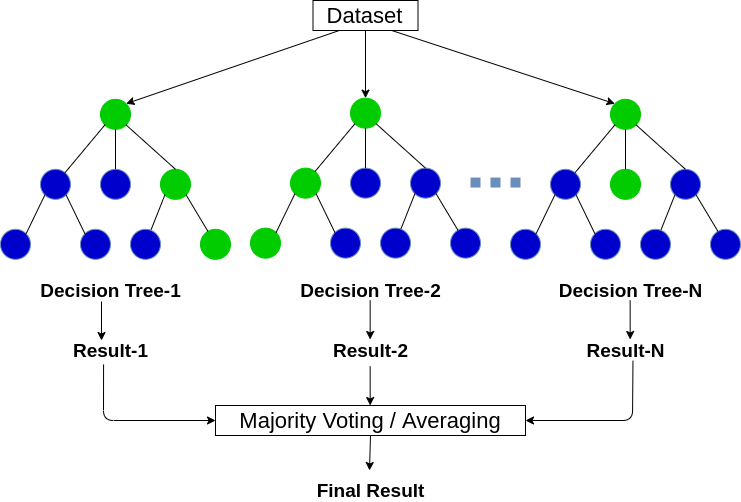
Decision Tree vs. Random Forest - Which Algorithm Should you Use? |Bagging

                                                          Image Source: Google Images

2. Why is Random Forest Algorithm popular?

Random Forest is one of the most popular and widely used machine learning algorithms for classification problems. It can also be used for the regression problem statements but it mainly performs well on the classification model.

It has become a lethal weapon for modern data scientists to refine the predictive model. The best part of the algorithm is that there are very few assumptions attached to it so data preparation is less challenging which results in time-saving. It’s listed as a top algorithm (with ensembling) that is popular among the Kaggle Competitions.

3. Can Random Forest Algorithm be used both for Continuous and Categorical Target Variables?

Yes, Random Forest can be used for both continuous and categorical target (dependent) variables.

In a random forest i.e, the combination of decision trees, the classification model refers to the categorical dependent variable, and the regression model refers to the numeric or continuous dependent variable.

4. What do you mean by Bagging?

Bagging, also known as Bootstrap-Aggregating, involves generating K’s new training data sets. Each new training data set picks a sample of data points with replacement (known as bootstrap samples) from the original data set.By sampling with replacement, means some of the data points may be repeated in each new training data set. The K models are fitted using the K bootstrap samples formed and then for predictions we combined the result of all trees by averaging the output (for regression) or voting (for classification).

Bagging - (Bootstrap aggregating) :: InBlog

                                                   Image Source: Google Images

5. Explain the working of the Random Forest Algorithm.

The steps that are included while performing the random forest algorithm are as follows:Step-1: Pick K random records from the dataset having a total of N records.

Step-2: Build and train a decision tree model on these K records.

Step-3: Choose the number of trees you want in your algorithm and repeat steps 1 and 2.

Step-4: In the case of a regression problem, for an unseen data point, each tree in the forest predicts a value for output. The final value can be calculated by taking the mean or average of all the values predicted by all the trees in the forest.

and, in the case of a classification problem, each tree in the forest predicts the class to which the new data point belongs. Finally, the new data point is assigned to the class that has the maximum votes among them i.e, wins the majority vote.

6. Why do we prefer a Forest (collection of Trees) rather than a single Tree?

While building a machine learning model, our aim is to generalize the model properly for giving predictions on unseen data.The problem of overfitting takes place when we have a flexible model. A flexible model is having high variance because the learned parameters like the structure of the decision tree, etc will vary with the training data. On the contrary, an inflexible model is said to have a high bias as it makes assumptions about the training data and an inflexible model may not have the capacity to fit even the training data and in both situations, the model has high variance, and high bias implies the model is not able to generalize new and unseen data points properly.

So, we have to build a model carefully by keeping the bias-variance tradeoff in mind.

The main reason for the overfitting of the decision tree due to not put the limit on the maximum depth of the tree is because it has unlimited flexibility, which means it keeps growing unless, for every single observation, there is one leaf node present.

Moreover, instead of limiting the depth of the tree which results in reduced variance and an increase in bias, we can combine many decision trees that eventually convert into a forest, known as a single ensemble model (known as the random forest).

7. What do you mean by Bootstrap Sample?

It is basically random with the replacement sampling method.For Example, Suppose we have a box of lottery tickets in which there are 100 unique numbers from 0 to 99. We want to select a random sample of tickets from the box. If we put the ticket back in the box, it may be selected more than once. Therefore, in this process, we are picking the samples randomly from the box with replacement.

Bootstrap Sampling Procedure The classical procedure of bootstrapping... | Download Scientific Diagram Bagging

                                               Image Source: Google Images

8. What is Out-of-Bag Error?

Out-of-Bag is equivalent to validation or test data. In random forests, there is no need for a separate testing dataset to validate the result. It is calculated internally, during the algorithm run, in the following manner -As the forest is built on training data, each tree is tested on 1/3rd of the samples (36.8%) that are not used in building that tree (similar to the validation data set).

This is known as the out-of-bag error estimate which in short is an internal error estimate of a random forest as it is being constructed.

9. What does random refer to in ‘Random Forest’?

‘Random’ in Random Forest refers to mainly two processes –

  • Random observations to grow each tree.
  • Random variables selected for splitting at each node.

Random Record Selection: Each tree in the forest is trained on roughly 2/3rd of the total training data (exactly 63.2%) and here the data points are drawn at random with replacement from the original training dataset. This sample will act as the training set for growing the tree.

Random Variable Selection: Some independent variables(predictors) say, m are selected at random out of all the predictor variables, and the best split on this m is used to split the node.

NOTE:

  • By default, m is taken as the square root of the total number of predictors for classification whereas m is the total number of all predictors divided by 3 for regression problems.
  • The value of m remains constant during the algorithm run i.e, forest growing.

10. Why does the Random Forest algorithm not require split sampling methods?

Random Forest does not require a split sampling method to assess the accuracy of the model.This is because it performs internal testing on 2/3rd of the available training data that is used to grow each tree and the remaining one-third portion of training data is always used to calculate out-of-bag error to compute the model performance.

11. List down the features of Bagged Trees.

The main features of Bagged Trees are as follows:

1. Reduces variance by averaging the ensemble’s results.

2. The resulting model uses the entire feature space when considering node splits.

3. It allows the trees to grow without pruning, reducing the tree-depth sizes which result in high variance but lower bias, which can help improve the prediction power.

12. What are the Limitations of Bagging Trees?

The major limitation of bagging trees is that it uses the entire feature space when creating splits in the trees.Suppose from all the variables within the feature space, some are indicating certain predictions, so there is a risk of having a forest of correlated trees, which actually increases bias and reduces variance. So, our objective is not achieved due to these issues.

13. List down the factors on which the forest error rate depends upon.

The forest error rate in Random forest depends on the following two factors:1. How correlated the two trees in the forest are i.e, 

The correlation between any two different trees in the forest. Increasing the correlation increases the forest error rate.

2. How strong each individual tree in the forest is i.e, 

The strength of each individual tree in the forest. In a forest, a tree having a low error rate is considered a strong classifier. Increasing the strength of the individual trees eventually leads to a decrement in the forest error rate.

Moreover, reducing the value of mtry i.e, the number of random variables used in each tree reduces both the correlation and the strength. Increasing it increases both. So, in between, there exists an “optimal” range of mtry which is usually quite a wide range.

Using the OOB error rate, a value of mtry can quickly be found in the range. This parameter is only adjustable from which random forests are somewhat sensitive.

14. How does a Random Forest Algorithm give predictions on an unseen dataset?

After training the algorithm, each tree in the forest gives a classification on leftover data (OOB), and we say the tree “votes” for that class. Then finally, the forest chooses the classification having the most votes over all the trees in the forest.For a binary dependent variable, the vote will be either YES or NO, and finally, it will count up the YES votes. This is the Random Forest (RF) score and the percent YES votes received is the predicted probability. In the regression case, it is the average of the dependent variable.

For example, suppose we fit 500 trees in a forest, and a case is out-of-bag in 200 of them:

  • 160 trees vote class 1
  • 40 trees vote class 2

In this case, the RF score is class1 since the probability for that case would be 0.8 which is 160/200. Similarly, it would be an average of the target variable for the regression problem.

15. Prove that in the Bagging method only about 63% of the total original examples (total training set) appear in any of sampled bootstrap datasets. Provide proper justification.

The detailed explanation of the proof is as follows:

Input: n labelled training examples S = {(xi, yi)},i = 1,..,n

Suppose we select n samples out of n with replacement to get a training set Si still different from working with the entire training set.

Pr(Si = S) = n!/nn (very small number, exponentially small in n)

Pr( (xi,yi) not in Si ) = (1-1/n)n = e-1 ~ 0.37

Hence for large data sets, about 37% of the data set is left out!

PPT - Ensemble learning PowerPoint Presentation, free download - ID:2843482

                                          Image Source: Google Images

16. How to determine the overall OOB score for the classification problem statements in a Random Forest Algorithm?

For each tree, by using the leftover (36.8%) data, compute the misclassification rate, which is known as out of bag (OOB) error rate. Finally, we aggregate all the errors from all trees and we will determine the overall OOB error rate for the classification.For Example, If we grow 300 trees then on average a record will be OOB for about 37*3 =111 trees.

17. How does random forest define the Proximity (Similarity) between observations?

Random Forest defines proximity between two data points in the following way:

  • Initialize proximities to zeroes.
  • For any given tree, apply all the cases to the tree.
  • If case i and case j both end up in the same node, then proximity prox(ij) between i and j increases by one.
  • Accumulate over all trees in Random Forest and normalize by twice the number of trees in Random forest.

Finally, it creates a proximity matrix i.e, a square matrix with entry as 1 on the diagonal and values between 0 and 1 in the off-diagonal positions. Proximities are close to 1 when the observations are “alike” and conversely the closer proximity to 0, implies the more dissimilar cases are.

18. What is the use of proximity matrix in the random forest algorithm?

A proximity matrix is used for the following cases :

  • Missing value imputation
  • Detection of outliers

19. List down the parameters used to fine-tune the Random Forest.

Two parameters that have to fine-tune to improve the predictions that are important in the random forest algorithm are as follows:

  • Number of trees used in the forest (n_tree)
  • Number of random variables used in each of the trees in the forest (mtry)

20. How to find an optimal value of the hyperparameter “ n_tree”?

To find an optimal value of n_tree, we first fix the value of mtry to the default value (sqrt of the total number of all predictors) and search for the optimal n_tree value.To find the value of n_tree (number of trees) that corresponds to a stable classifier, we train random forest models with different values of n_tree such as (100, 200, 300….,1,000).

As a result, we have 10 Random Forest classifiers in our hand for each value of n_tree, record the OOB error rate and see that value of n_tree where the out-of-bag error rate stabilizes and reaches its minimum value.

21. How to find an optimal value of the hyperparameter “mtry”?

The following two ways can be used to find the optimal value of mtry :1. Apply a similar procedure as in finding the optimal n_tree such that random forest is run 10 times. The optimal number of predictors selected for split is selected for which the out-of-bag error rate stabilizes and reaches the minimum.

2. In this method, we are doing the experiment by including the values such as the square root of the total number of all predictors, half of this square root value, and twice of the square root value, etc and at the same time check which value of mtry gives the maximum area under the curve.

For Example, Suppose we have 1000 predictors, then the number of predictors to select for each node would be 16, 32, and 64.

22. How do Random Forests select the Important Features?

Sometimes random forests can also be used to determine the importance of variables i.e, rank in a regression or classification problem.The factors that are used to find the rank of the variables are as follows:

  • Mean Decrease Accuracy: If we drop that variable, how much the model accuracy decreases.
  • Mean Decrease Gini: This measure of variable importance is used for the calculation of splits in trees based on the Gini impurity index.

Conclusion: The higher the value of mean decrease accuracy or mean decrease Gini score, the higher the importance of the variable in the model.

23. Explain the steps of calculating Variable Importance in Random Forest.

The steps for calculating variable importance in Random Forest Algorithm are as follows:

1. For each tree grown in a random forest, find the number of votes for the correct class in out-of-bag data.

2. Now perform random permutation of a predictor’s values (let’s say variable-k) in the OOB data and then check the number of votes for the correct class. By “random permutation of a predictor’s values”, it means changing the order of values (shuffling).

3. At this step, we subtract the number of votes for the correct class in the variable-k-permuted data from the number of votes for the correct class in the original OOB data.

4. Now, the raw importance score for variable k is the average of this number over all trees in the forest. Then, we normalized the score by taking the standard deviation.

5. Variables having large values for this score are ranked as more important as building a current model without original values of a variable gives a worse prediction, which means the variable is important.

24. List down some of the shortcomings of the Random Forest Algorithm.

The shortcomings of the Random Forest algorithm are as follows:

1. Random Forests aren’t good at generalizing cases with completely new data.

For Example, If we know that the cost of one ice cream is $1, 2 ice-creams cost $2, and 3 ice-creams cost $3, then how much do 10 ice-creams cost? In such cases, Linear regression models can easily figure this out, while a Random Forest has no way of finding the answer.

2. Random forests are biased towards the categorical variable having multiple levels or categories. It is because the feature selection technique is based on the reduction in impurity and is biased towards preferring variables with more categories so the variable selection is not accurate for this type of data.

25. List down the advantages and disadvantages of the Random Forest Algorithm.

Advantages:

  • Random Forest is unbiased as we train multiple decision trees and each tree is trained on a subset of the same training data.
  • It is very stable since if we introduce the new data points in the dataset, then it does not affect much as the new data point impacts one tree, and is pretty hard to impact all the trees.
  • Also, it works well when you have both categorical and numerical features in the problem statement.
  • It performs very well, with missing values in the dataset.

Disadvantages:

  • Complexity is the major disadvantage of this algorithm. More computational resources are required and also results in a large number of decision trees combined together.
  • Due to their complexity, training time is more compared to other algorithms.

Test your knowledge and enhance your skills with our ‘Mastering Random Forest and Bagging Techniques‘ course! Dive into 25 challenging questions on the Random Forest algorithm and gain the confidence you need to excel in your data science career—enroll now and take your expertise to the next level!

End Notes

Thanks for reading!

I hope you enjoyed the questions and were able to test your knowledge about Random Forest Algorithm.

If you liked this and want to know more, go visit my other articles on Data Science and Machine Learning by clicking on the Link

Please feel free to contact me on Linkedin, Email.

Something not mentioned or want to share your thoughts? Feel free to comment below And I’ll get back to you.

About the author

Chirag Goyal

Currently, I am pursuing my Bachelor of Technology (B.Tech) in Computer Science and Engineering from the Indian Institute of Technology Jodhpur(IITJ). I am very enthusiastic about Machine learning, Deep Learning, and Artificial Intelligence.

The media shown in this article are not owned by Analytics Vidhya and are used at the Author’s discretion.

Chirag Goyal
Chirag Goyal

I am a B.Tech. student (Computer Science major) currently in the pre-final year of my undergrad. My interest lies in the field of Data Science and Machine Learning. I have been pursuing this interest and am eager to work more in these directions. I feel proud to share that I am one of the best students in my class who has a desire to learn many new things in my field.

Free Courses

Generative AI 4.7

Generative AI - A Way of Life

Explore Generative AI for beginners: create text and images, use top AI tools, learn practical skills, and ethics.
Large Language Models 4.5

Getting Started with Large Language Models

Master Large Language Models (LLMs) with this course, offering clear guidance in NLP and model training made simple.
Prompt Engineering 4.6

Building LLM Applications using Prompt Engineering

This free course guides you on building LLM apps, mastering prompt engineering, and developing chatbots with enterprise data.
LlamaIndex 4.8

Improving Real World RAG Systems: Key Challenges & Practical Solutions

Explore practical solutions, advanced retrieval strategies, and agentic RAG systems to improve context, relevance, and accuracy in AI-driven applications.
RAG systems using LlamaIndex 4.7

Microsoft Excel: Formulas & Functions

Master MS Excel for data analysis with key formulas, functions, and LookUp tools in this comprehensive course.

Recommended Articles

Responses From Readers

Clear

Siya
Siya

Thanku very much for all important questions. Helpful articles.

123

Write for us

Write, captivate, and earn accolades and rewards for your work
  • Reach a Global Audience
  • Get Expert Feedback
  • Build Your Brand & Audience
  • Cash In on Your Knowledge
  • Join a Thriving Community
  • Level Up Your Data Science Game
imag

We use cookies essential for this site to function well. Please click to help us improve its usefulness with additional cookies. Learn about our use of cookies in our Privacy Policy & Cookies Policy.

Show details