Must for Data Scientists & Analysts: Brain Training for Analytical Thinking

Introduction

Let’s start this article with a small exercise. Take a pen and paper and write the answer as it comes to your mind. No thinking twice and you shouldn’t take more than 15 seconds to do it.

On this paper, please write the answer to “What are the skills required to become a successful data scientist?”

A lot of you would have written coding, knowledge of analytics tools, statistics etc. All of these are definitely required to be a successful data scientist, but they are not sufficient.

One of the most important skill differentiating a good analyst / data scientist from the bad one is the ability to take complex problems, put a framework around it, make simplifying assumptions, analyze the problem and then come up with solutions. And analytics tools are just a medium to do so.

In today’s article we will take a case study and see this process of problem solving in structured manner.

What you’ll learn ?

Here you’ll find practice problems to train your brain think analytically while solving complex problems. This brain training will not only introduce you to a new approach to solve problems but will also help you to think faster while dealing with numbers!

My previous article on how to train your mind for analytical thinking? should give you a good head start.

Practice Problem

Here’s is my daily routine:

I get ready and leave home for office at sharp 10:30 AM every working day. Considering the amount of work I got to finish on some days, I try to reach early by driving faster than other days (obviously in safe limits).

However, since last 5 days, I’ve observed that I reach office almost at the same time, irrespective of my average speed between traffic lights. This makes me wonder, whether the time taken from my home to office is dependent on my velocity or not? In other words, the total average velocity adjusted by the traffic lights to the same level, and does not depend on the velocity we drive the car!

 

Take the Test: Should I become a Data Scientist ?

To explain you better, consider a simplistic scenario:

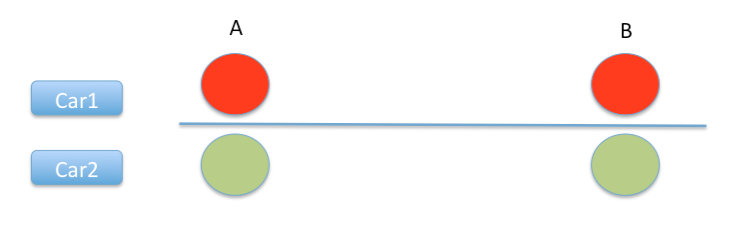
Two cars start from point A which is the first traffic signal. Point B is a traffic signal with a halt time of 60 sec and drive time of 20 sec. The distance between A and B is 600m. Car1 starts at 5m/sec and Car2 starts at 6m/sec. Who will cross the traffic light first? Here are the assumptions:

1. Traffic lights are configured for average speeds, it becomes green 120 seconds (600 m / 5 m/sec) after the first signal turns green.

2. Traffic lights are green for 20 seconds and red for 60 seconds (20 * 3)

Assume both cars start at 0 sec.

Time taken for Car1 to reaches signal B = 600/6 = 100sec

Time taken for Car2 to reaches signal B = 600/5 = 120sec

Light is green at (40,60) ; (120,140) ; (200,220) ; (280,300)

Hence, cars reaching point B in 61 sec and one reaching at 140 second show no difference in terms of passing through the second signal. Let’s calculate the min and max speeds which will show no difference amongst the two lights scenario :

Minimum speed = 600m / 120sec = 5 m/sec = 18 km/hr

Minimum speed = 600m / 61sec = 9.8m/sec= 35 km/hr

It does not matter whether you drive at 18 km/hr or 35 km/hr in this scenario, you will cross the second signal (B) at the same time. In general, it is difficult to drive in such wide range of speeds in peak time traffic and hence my concerns looks logical now. I probably have no control on the time I will take to reach office (obviously this is over simplification of the problem).

Let’s make it more complex…!

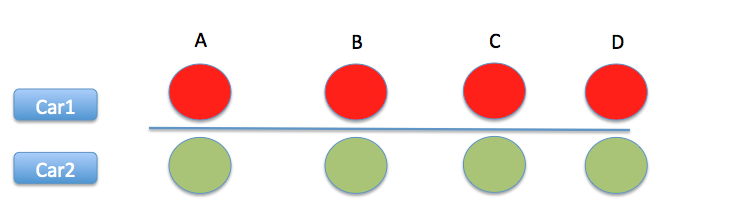
Now we have 4 signals A,B,C and D. Same two cars start from A at the time 0 sec. Distances between AB , BC and CD are same. The question is now, who will cross the signal D first.

Without going into mathematics, the answer is very straight forward.  If both will cross B at the same time, A – B pair is the same as B-C pair which is in turn same as C-D pair. Hence both the car will cross D at the same time. The scenario is actually more extreme, the car which maintains an average speed of 18 km/hr and the one at 35 km/hr will cross D at the same time. This further strengthens my hypothesis.

Question again boils down to :

“Am I just a helpless puppet in traffic police’s hand while driving to my office ? “

Let’s try to generalize it into a parametric equation

Actual scenario is too difficult to generalize in this article, so let’s ground a few assumptions :

1. Traffic lights turn green for time t sec and becomes red for time 3t sec

2. Average speed of a vehicle on road is v m/sec

3. The challenger to the average vehicle drives at a velocity x times v m/sec

4. All roads have a length of l meters

By now, we already know, it hardly matters if we solve for one pair of traffic light or more. If the faster driver is able to sneak through the traffic light in a green signal before the average vehicle, it will make a difference or else not.

Hence, the difference in time required to make this happen will be 3t. Following is the final equation we are solving for :

Time taken by average vehicle : l/v sec

Time taken by faster vehicle : l/vx sec

It simplifies to ;

 l/ v  - l/vx  > 3t

Given x , v, l and t are all positive, this can be further simplified to :

 xl  - l - 3tvx > 0

x (l - 3tv)> l

Here is a JACKPOT! We know that l is always positive, hence to make the above equation practical, both x and (l – 3tv) have to be positive. This means if 3tv becomes more than l, you have no chance of beating traffic lights. For instance, if t = 30 sec, v = 5 m/sec and l = 145 m, you simply cannot beat the odds, even if you ride on speed of GUN shot!

Let’s assume a few parameters and understand the equation further:

Say, l = 600 m. The equation becomes :

 x (200 - tv) > 200

So, here are a few thumb rules to make it possible to beat the Traffic signals :

1. Minimize t (cycle of traffic light) : It is possible to beat traffic light in quick traffic localities where it turns Green – Red in quick time.

2. Minimize v (the average velocity of the road ) :  If the average velocity on road is exceptionally low, we can beat these slow drivers if we drive fast (Duh!)

3. Maximize x (Faster multiplier) : If we drive super fast, we can still win the race. But notice if v*t becomes more than 200, you have no chance of getting

Don’t miss: Introducing the art of structured thinking and analyzing

Let’s try to visualize a few relations

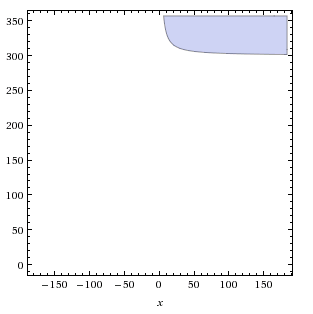
Average t in Bangalore is about 20 seconds and average speed is 5m/sec. Hence the equation becomes :

x(l - 300) > l

As seen from the above graph, if x and l are high enough to fall into the shaded region, we have a chance to beat the traffic light.

Let’s summarize our findings

1. There is no point of driving fast on a lane where 3 * Green light time * average velocity is more than the length of the road.

2. Beating traffic is possible if following are in our favor :

a. High x . We drive really fast (not a safe option)

b. High l. For instance driving fast on a highway makes sense

c. Low t : No point of driving fast on a high timer traffic signals road

d. Low v : If the average velocity on the road is really low, we can beat them. We already knew that!

End Notes

I hope, you enjoyed solving this traffic problem. I’m sure it would have challenged your thinking which was our motive. Right ?

In this article, using a case of traffic light and some elementary physics concepts I have explained the necessary skill required to build a unshakable foundation to become a data scientist.

Did you enjoy reading this article? Have you wondered over this question before? Do you think you can improvise these calculations further to make it more realistic?

If you like what you just read & want to continue your analytics learning, subscribe to our emails, follow us on twitter or like our facebook page.

Tavish Srivastava

Tavish Srivastava, co-founder and Chief Strategy Officer of Analytics Vidhya, is an IIT Madras graduate and a passionate data-science professional with 8+ years of diverse experience in markets including the US, India and Singapore, domains including Digital Acquisitions, Customer Servicing and Customer Management, and industry including Retail Banking, Credit Cards and Insurance. He is fascinated by the idea of artificial intelligence inspired by human intelligence and enjoys every discussion, theory or even movie related to this idea.