Interview Prep
Career
GenAI
Prompt Engg
ChatGPT
LLM
Langchain
RAG
AI Agents
Machine Learning
Deep Learning
GenAI Tools
LLMOps
Python
NLP
SQL
AIML Projects

Reading list

Machine Learning Basics for a Newbie
6 Steps of Machine learning Lifecycle Introduction to Predictive Modeling
Introduction to Exploratory Data Analysis & Data Insights Descriptive Statistics Inferential Statistics How to Understand Population Distributions?
Reading Data Files into Python Different Variable Datatypes
Probability for Data Science Basic Concepts of Probability Axioms of Probability Conditional Probability
Central Tendencies for Continuous Variables Spread of Data KDE plots for Continuous Variable Overview of Distribution for Continuous variables Normal Distribution Skewed Distribution Skeweness and Kurtosis Distribution for Continuous Variable
Central Tendencies for Categorical Variables Understanding Discrete Distributions Performing EDA on Categorical Variables
Dealing with Missing Values Understanding Outliers Identifying Outliers in Data Outlier Detection in Python Outliers Detection Using IQR, Z-score, LOF and DBSCAN
Sample and Population Central Limit Theorem Confidence Interval and Margin of Error
Bivariate Analysis Introduction
Covariance Pearson Correlation Spearman's Correlation & Kendall's Tau Correlation versus Causation Tabular and Graphical methods for Bivariate Analysis Performing Bivariate Analysis on Continuous-Continuous Variables
Tabular and Graphical methods for Continuous-Categorical Variables Introduction to Hypothesis Testing P-value Two sample Z-test T-test T-test vs Z-test Performing Bivariate Analysis on Continuous-Catagorical variables
Chi-Squares Test Bivariate Analysis on Categorical Categorical Variables
Multivariate Analysis A Comprehensive Guide to Data Exploration The Data Science behind IPL
Supervised Learning vs Unsupervised Learning Reinforcement Learning Generative and Descriminative Models Parametric and Non Parametric model
Machine Learning Pipeline Preparing Dataset Build a Benchmark Model: Regression Build a Benchmark Model: Classification
Evaluation Metrics for Machine Learning Everyone should know Confusion Matrix Accuracy Precision and Recall AUC-ROC Log Loss R2 and Adjusted R2
Dealing with Missing Values Replacing Missing Values Imputing Missing Values in Data Working with Categorical Variables Working with Outliers Preprocessing Data for Model Building
Understanding Cost Function Understanding Gradient Descent Math Behind Gradient Descent Assumptions of Linear Regression Implement Linear Regression from Scratch Train Linear Regression in Python Implementing Linear Regression in R Diagnosing Residual Plots in Linear Regression Models Generalized Linear Models Introduction to Logistic Regression Odds Ratio Implementing Logistic Regression from Scratch Introduction to Scikit-learn in Python Train Logistic Regression in python Multiclass using Logistic Regression How to use Multinomial and Ordinal Logistic Regression in R ? Challenges with Linear Regression Introduction to Regularisation Implementing Regularisation Ridge Regression Lasso Regression
Introduction to K Nearest Neighbours Determining the Right Value of K in KNN Implement KNN from Scratch Implement KNN in Python
Bias Variance Tradeoff Introduction to Overfitting and Underfitting Visualizing Overfitting and Underfitting Selecting the Right Model What is Validation? Hold-Out Validation Understanding K Fold Cross Validation
Introduction to Feature Selection Feature Selection Algorithms Missing Value Ratio Low Variance Filter High Correlation Filter Backward Feature Elimination Forward Feature Selection Implement Feature Selection in Python Implement Feature Selection in R
Introduction to Decision Tree Purity in Decision Tree Terminologies Related to Decision Tree How to Select Best Split Point in Decision Tree? Chi-Squares Information Gain Reduction in Variance Optimizing Performance of Decision Tree Train Decision Tree using Scikit Learn Pruning of Decision Trees
Introduction to Feature Engineering Feature Transformation Feature Scaling Feature Engineering Frequency Encoding Automated Feature Engineering: Feature Tools
Introduction to Naive Bayes Conditional Probability and Bayes Theorem Introduction to Bayesian Adjustment Rating: The Incredible Concept Behind Online Ratings! Working of Naive Bayes Math behind Naive Bayes Types of Naive Bayes Implementation of Naive Bayes
Understanding how to solve Multiclass and Multilabled Classification Problem Evaluation Metrics: Multi Class Classification
Introduction to Ensemble Techniques Basic Ensemble Techniques Implementing Basic Ensemble Techniques Finding Optimal Weights of Ensemble Learner using Neural Network Why Ensemble Models Work well?
Introduction to Stacking Implementing Stacking Variants of Stacking Implementing Variants of Stacking Introduction to Blending Bootstrap Sampling Introduction to Random Sampling Hyper-parameters of Random Forest Implementing Random Forest Out-of-Bag (OOB) Score in the Random Forest IPL Team Win Prediction Project Using Machine Learning Introduction to Boosting Gradient Boosting Algorithm Math behind GBM Implementing GBM in python Regularized Greedy Forests Extreme Gradient Boosting Implementing XGBM in python Tuning Hyperparameters of XGBoost in Python Implement XGBM in R/H2O Adaptive Boosting Implementing Adaptive Boosing LightGBM Implementing LightGBM in Python Catboost Implementing Catboost in Python
Different Hyperparameter Tuning methods Implementing Different Hyperparameter Tuning methods GridsearchCV RandomizedsearchCV Bayesian Optimization for Hyperparameter Tuning Hyperopt
Understanding SVM Algorithm SVM Kernels In-depth Intuition and Practical Implementation SVM Kernel Tricks Kernels and Hyperparameters in SVM Implementing SVM from Scratch in Python and R
Introduction to Principal Component Analysis Steps to Perform Principal Compound Analysis Computation of Covariance Matrix Finding Eigenvectors and Eigenvalues Implementing PCA in python Visualizing PCA A Brief Introduction to Linear Discriminant Analysis Introduction to Factor Analysis
Introduction to Clustering Applications of Clustering Evaluation Metrics for Clustering Understanding K-Means Implementation of K-Means in Python Implementation of K-Means in R Choosing Right Value for K Profiling Market Segments using K-Means Clustering Hierarchical Clustering Implementation of Hierarchial Clustering DBSCAN Defining Similarity between clusters Build Better and Accurate Clusters with Gaussian Mixture Models
Understand Basics of Recommendation Engine with Case Study
8 Ways to Improve Accuracy of Machine Learning Models
Introduction to Dask Working with CuML
Introduction to Machine Learning Interpretability Framework and Interpretable Models model Agnostic Methods for Interpretability Implementing Interpretable Model Understanding SHAP Out-of-Core ML Introduction to Interpretable Machine Learning Models Model Agnostic Methods for Interpretability Game Theory & Shapley Values
Introduction to Machine Learning Interpretability Framework and Interpretable Models model Agnostic Methods for Interpretability Implementing Interpretable Model Understanding SHAP Out-of-Core ML Introduction to Interpretable Machine Learning Models Model Agnostic Methods for Interpretability Game Theory & Shapley Values
Introduction to AutoML Implementation of MLBox Introduction to PyCaret TPOT Auto-Sklearn EvalML
Pickle and Joblib Introduction to Model Deployment
Deploying Machine Learning Model using Streamlit Deploying ML Models in Docker Deploy Using Streamlit Deploy on Heroku Deploy Using Netlify Introduction to Amazon Sagemaker Setting up Amazon SageMaker Using SageMaker Endpoint to Generate Inference Deploy on Microsoft Azure Cloud Introduction to Flask for Model Deploying ML model using Flask
Model Deployment in Android Model Deployment in Iphone

Practical guide to implement machine learning with CARET package in R (with practice problem)

saurav kaushik
saurav kaushik Last Updated : 05 Jul, 2020
13 min read

Introduction

One of the biggest challenge beginners in machine learning face is which algorithms to learn and focus on. In case of R, the problem gets accentuated by the fact that various algorithms would have different syntax, different parameters to tune and different requirements on the data format. This could be too much for a beginner.

So, then how do you transform from a beginner to a data scientist building hundreds of models and stacking them together? There certainly isn’t any shortcut but what I’ll tell you today will make you capable of applying hundreds of machine learning models without having to:

  • remember the different package names for each algorithm.
  • syntax of applying each algorithm.
  • parameters to tune for each algorithm.

All this has been made possible by the years of effort that have gone behind CARET ( Classification And Regression Training) which is possibly the biggest project in R. This package alone is all you need to know for solve almost any supervised machine learning problem. It provides a uniform interface to several machine learning algorithms and standardizes various other tasks such as Data splitting, Pre-processing, Feature selection, Variable importance estimation, etc.

To get an in-depth overview of various functionalities provided by Caret, you can refer to this article.

Today, we’ll work on the Loan Prediction problem-III to show you the power of Caret package.

P.S. While caret definitely simplifies the job to a degree, it can not take away the hard work and practice you need to put in to become a master at machine learning.

 

Table of Contents

  1. Getting started
  2. Pre-processing using Caret
  3. Splitting the data using Caret
  4. Feature selection using Caret
  5. Training models using Caret
  6. Parameter tuning using Caret
  7. Variable importance estimation using Caret
  8. Making predictions using Caret

 

1. Getting started

To put in simple words, Caret is essentially a wrapper for 200+ machine learning algorithms. Additionally, it provides several features which makes it a one stop solution for all the modeling needs for supervised machine learning problems.

Caret tries not to load all the packages it depends upon at the start. Instead, it loads them only when the packages are needed. But it does assume that you already have all the algorithms installed on your system.

To install Caret on your system, use the following command. Heads up: It might take some time:

> install.packages("caret", dependencies = c("Depends", "Suggests"))

Now, let’s get started using caret package on Loan Prediction 3 problem:

#Loading caret package library("caret") #Loading training data train<-read.csv("train_u6lujuX_CVtuZ9i.csv",stringsAsFactors = T) #Looking at the structure of caret package. str(train) #'data.frame':         614 obs. of  13 variables: #$ Loan_ID          : Factor w/ 614 levels "LP001002","LP001003",..: 1 2 3 4 5 6 7 8 9 #10 .. #$ Gender           : Factor w/ 3 levels "","Female","Male": 3 3 3 3 3 3 3 3 3 3 ... #$ Married          : Factor w/ 3 levels "","No","Yes": 2 3 3 3 2 3 3 3 3 3 ... #$ Dependents       : Factor w/ 5 levels "","0","1","2",..: 2 3 2 2 2 4 2 5 4 3 ... #$ Education        : Factor w/ 2 levels "Graduate","Not Graduate": 1 1 1 2 1 1 2 1 1 #1 ... #$ Self_Employed    : Factor w/ 3 levels "","No","Yes": 2 2 3 2 2 3 2 2 2 2 ... #$ ApplicantIncome  : int  5849 4583 3000 2583 6000 5417 2333 3036 4006 12841 #... #$ CoapplicantIncome: num  0 1508 0 2358 0 ... #$ LoanAmount       : int  NA 128 66 120 141 267 95 158 168 349 ... #$ Loan_Amount_Term : int  360 360 360 360 360 360 360 360 360 360 ... #$ Credit_History   : int  1 1 1 1 1 1 1 0 1 1 ... #$ Property_Area    : Factor w/ 3 levels "Rural","Semiurban",..: 3 1 3 3 3 3 3 2 3 2 #... #$ Loan_Status      : Factor w/ 2 levels "N","Y": 2 1 2 2 2 2 2 1 2 1 ...

In this problem, we have to predict the Loan Status of a person based on his/ her profile.

 

2. Pre-processing using Caret

We need to pre-process our data before we can use it for modeling. Let’s check if the data has any missing values:

sum(is.na(train)) #[1] 86

Next, let us use Caret to impute these missing values using KNN algorithm. We will predict these missing values based on other attributes for that row. Also, we’ll scale and center the numerical data by using the convenient preprocess() in Caret.

#Imputing missing values using KNN.Also centering and scaling numerical columns preProcValues <- preProcess(train, method = c("knnImpute","center","scale")) library('RANN') train_processed <- predict(preProcValues, train) sum(is.na(train_processed)) #[1] 0

It is also very easy to use one hot encoding in Caret to create dummy variables for each level of a categorical variable. But first, we’ll convert the dependent variable to numerical.

#Converting outcome variable to numeric train_processed$Loan_Status<-ifelse(train_processed$Loan_Status=='N',0,1) id<-train_processed$Loan_ID train_processed$Loan_ID<-NULL #Checking the structure of processed train file str(train_processed) #'data.frame':         614 obs. of  12 variables: #$ Gender           : Factor w/ 3 levels "","Female","Male": 3 3 3 3 3 3 3 3 3 3 ... #$ Married          : Factor w/ 3 levels "","No","Yes": 2 3 3 3 2 3 3 3 3 3 ... #$ Dependents       : Factor w/ 5 levels "","0","1","2",..: 2 3 2 2 2 4 2 5 4 3 ... #$ Education        : Factor w/ 2 levels "Graduate","Not Graduate": 1 1 1 2 1 1 2 1 1 #1 ... #$ Self_Employed    : Factor w/ 3 levels "","No","Yes": 2 2 3 2 2 3 2 2 2 2 ... #$ ApplicantIncome  : num  0.0729 -0.1343 -0.3934 -0.4617 0.0976 ... #$ CoapplicantIncome: num  -0.554 -0.0387 -0.554 0.2518 -0.554 ... #$ LoanAmount       : num  0.0162 -0.2151 -0.9395 -0.3086 -0.0632 ... #$ Loan_Amount_Term : num  0.276 0.276 0.276 0.276 0.276 ... #$ Credit_History   : num  0.432 0.432 0.432 0.432 0.432 ... #$ Property_Area    : Factor w/ 3 levels "Rural","Semiurban",..: 3 1 3 3 3 3 3 2 3 2 #... #$ Loan_Status      : num  1 0 1 1 1 1 1 0 1 0 ...

Now, creating dummy variables using one hot encoding:

#Converting every categorical variable to numerical using dummy variables dmy <- dummyVars(" ~ .", data = train_processed,fullRank = T) train_transformed <- data.frame(predict(dmy, newdata = train_processed)) #Checking the structure of transformed train file str(train_transformed) #'data.frame':         614 obs. of  19 variables: #$ Gender.Female          : num  0 0 0 0 0 0 0 0 0 0 ... #$ Gender.Male            : num  1 1 1 1 1 1 1 1 1 1 ... #$ Married.No             : num  1 0 0 0 1 0 0 0 0 0 ... #$ Married.Yes            : num  0 1 1 1 0 1 1 1 1 1 ... #$ Dependents.0           : num  1 0 1 1 1 0 1 0 0 0 ... #$ Dependents.1           : num  0 1 0 0 0 0 0 0 0 1 ... #$ Dependents.2           : num  0 0 0 0 0 1 0 0 1 0 ... #$ Dependents.3.          : num  0 0 0 0 0 0 0 1 0 0 ... #$ Education.Not.Graduate : num  0 0 0 1 0 0 1 0 0 0 ... #$ Self_Employed.No       : num  1 1 0 1 1 0 1 1 1 1 ... #$ Self_Employed.Yes      : num  0 0 1 0 0 1 0 0 0 0 ... #$ ApplicantIncome        : num  0.0729 -0.1343 -0.3934 -0.4617 0.0976 ... #$ CoapplicantIncome      : num  -0.554 -0.0387 -0.554 0.2518 -0.554 ... #$ LoanAmount             : num  0.0162 -0.2151 -0.9395 -0.3086 -0.0632 ... #$ Loan_Amount_Term       : num  0.276 0.276 0.276 0.276 0.276 ... #$ Credit_History         : num  0.432 0.432 0.432 0.432 0.432 ... #$ Property_Area.Semiurban: num  0 0 0 0 0 0 0 1 0 1 ... #$ Property_Area.Urban    : num  1 0 1 1 1 1 1 0 1 0 ... #$ Loan_Status            : num  1 0 1 1 1 1 1 0 1 0 ... #Converting the dependent variable back to categorical train_transformed$Loan_Status<-as.factor(train_transformed$Loan_Status)

Here, “fullrank=T” will create only (n-1) columns for a categorical column with n different levels. This works well particularly for the representing categorical predictors like gender, married, etc. where we only have two levels: Male/Female, Yes/No, etc. because 0 can be used to represent one class while 1 represents the other class in same column.

 

3. Splitting data using caret

We’ll be creating a cross-validation set from the training set to evaluate our model against. It is important to rely more on the cross-validation set for the actual evaluation of your model otherwise you might end up overfitting the public leaderboard.

We’ll use createDataPartition() to split our training data into two sets : 75% and 25%. Since, our outcome variable is categorical in nature, this function will make sure that the distribution of outcome variable classes will be similar in both the sets.

#Spliting training set into two parts based on outcome: 75% and 25% index <- createDataPartition(train_transformed$Loan_Status, p=0.75, list=FALSE) trainSet <- train_transformed[ index,] testSet <- train_transformed[-index,] #Checking the structure of trainSet str(trainSet) #'data.frame':         461 obs. of  19 variables: #$ Gender.Female          : num  0 0 0 0 0 0 0 0 0 0 ... #$ Gender.Male            : num  1 1 1 1 1 1 1 1 1 1 ... #$ Married.No             : num  1 0 0 0 1 0 0 0 0 0 ... #$ Married.Yes            : num  0 1 1 1 0 1 1 1 1 1 ... #$ Dependents.0           : num  1 0 1 1 1 0 1 0 0 0 ... #$ Dependents.1           : num  0 1 0 0 0 0 0 0 1 0 ... #$ Dependents.2           : num  0 0 0 0 0 1 0 0 0 1 ... #$ Dependents.3.          : num  0 0 0 0 0 0 0 1 0 0 ... #$ Education.Not.Graduate : num  0 0 0 1 0 0 1 0 0 0 ... #$ Self_Employed.No       : num  1 1 0 1 1 0 1 1 1 1 ... #$ Self_Employed.Yes      : num  0 0 1 0 0 1 0 0 0 0 ... #$ ApplicantIncome        : num  0.0729 -0.1343 -0.3934 -0.4617 0.0976 ... #$ CoapplicantIncome      : num  -0.554 -0.0387 -0.554 0.2518 -0.554 ... #$ LoanAmount             : num  0.0162 -0.2151 -0.9395 -0.3086 -0.0632 ... #$ Loan_Amount_Term       : num  0.276 0.276 0.276 0.276 0.276 ... #$ Credit_History         : num  0.432 0.432 0.432 0.432 0.432 ... #$ Property_Area.Semiurban: num  0 0 0 0 0 0 0 1 1 0 ... #$ Property_Area.Urban    : num  1 0 1 1 1 1 1 0 0 1 ... #$ Loan_Status            : Factor w/ 2 levels "0","1": 2 1 2 2 2 2 2 1 1 2 ...

 

4. Feature selection using Caret

Feature selection is an extremely crucial part of modeling. To understand the importance of feature selection and various techniques used for feature selection, I strongly recommend that you to go through my previous article. For now, we’ll be using Recursive Feature elimination which is a wrapper method to find the best subset of features to use for modeling.

#Feature selection using rfe in caret
control <- rfeControl(functions = rfFuncs,                    method = "repeatedcv",                    repeats = 3,                    verbose = FALSE) outcomeName<-'Loan_Status' predictors<-names(trainSet)[!names(trainSet) %in% outcomeName] Loan_Pred_Profile <- rfe(trainSet[,predictors], trainSet[,outcomeName],                       rfeControl = control) Loan_Pred_Profile #Recursive feature selection #Outer resampling method: Cross-Validated (10 fold, repeated 3 times) #Resampling performance over subset size: #  Variables Accuracy  Kappa AccuracySD KappaSD Selected #4   0.7737 0.4127    0.03707 0.09962         #8   0.7874 0.4317    0.03833 0.11168         #16   0.7903 0.4527    0.04159 0.11526         #18   0.7882 0.4431    0.03615 0.10812         #The top 5 variables (out of 16): #  Credit_History, LoanAmount, Loan_Amount_Term, ApplicantIncome, CoapplicantIncome #Taking only the top 5 predictors predictors<-c("Credit_History", "LoanAmount", "Loan_Amount_Term", "ApplicantIncome", "CoapplicantIncome")

 

5. Training models using Caret

This is probably the part where Caret stands out from any other available package. It provides the ability for implementing 200+ machine learning algorithms using consistent syntax. To get a list of all the algorithms that Caret supports, you can use:

names(getModelInfo())
#[1] "ada"                 "AdaBag"              "AdaBoost.M1"         "adaboost"           #[5] "amdai"               "ANFIS"               "avNNet"              "awnb"               #[9] "awtan"               "bag"                 "bagEarth"            "bagEarthGCV"        #[13] "bagFDA"              "bagFDAGCV"           "bam"                 "bartMachine"        #[17] "bayesglm"            "bdk"                 "binda"               "blackboost"         #[21] "blasso"              "blassoAveraged"      "Boruta"              "bridge"              #…. #[205] "svmBoundrangeString" "svmExpoString"       "svmLinear"           "svmLinear2"         #[209] "svmLinear3"          "svmLinearWeights"    "svmLinearWeights2"   "svmPoly"            #[213] "svmRadial"           "svmRadialCost"       "svmRadialSigma"      "svmRadialWeights"   #[217] "svmSpectrumString"   "tan"                 "tanSearch"           "treebag"            #[221] "vbmpRadial"          "vglmAdjCat"          "vglmContRatio"       "vglmCumulative"     #[225] "widekernelpls"       "WM"                  "wsrf"                "xgbLinear"          #[229] "xgbTree"             "xyf"

To get more details of any model, you can refer here.

We can simply apply a large number of algorithms with similar syntax. For example, to apply, GBM, Random forest, Neural net and Logistic regression :

model_gbm<-train(trainSet[,predictors],trainSet[,outcomeName],method='gbm') model_rf<-train(trainSet[,predictors],trainSet[,outcomeName],method='rf') model_nnet<-train(trainSet[,predictors],trainSet[,outcomeName],method='nnet') model_glm<-train(trainSet[,predictors],trainSet[,outcomeName],method='glm')

You can proceed further tune the parameters in all these algorithms using the parameter tuning techniques.

 

6. Parameter tuning using Caret

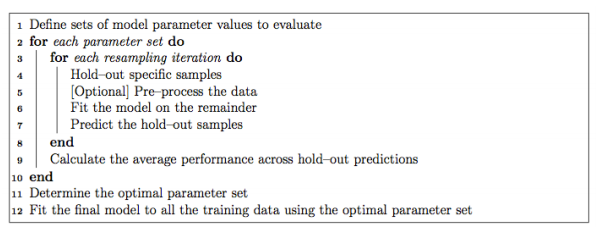
It’s extremely easy to tune parameters using Caret. Typically, parameter tuning in Caret is done as below:

caret-6

It is possible to customize almost every step in the tuning process. The resampling technique used for evaluating the performance of the model using a set of parameters in Caret by default is bootstrap, but it provides alternatives for using k-fold, repeated k-fold as well as Leave-one-out cross validation (LOOCV) which can be specified using trainControl(). In this example, we’ll be using 5-Fold cross-validation repeated 5 times.

fitControl <- trainControl(   method = "repeatedcv",   number = 5,   repeats = 5)

If the search space for parameters is not defined, Caret will use 3 random values of each tunable parameter and use the cross-validation results to find the best set of parameters for that algorithm. Otherwise, there are two more ways to tune parameters:

6.1.Using tuneGrid

To find the parameters of a model that can be tuned, you can use

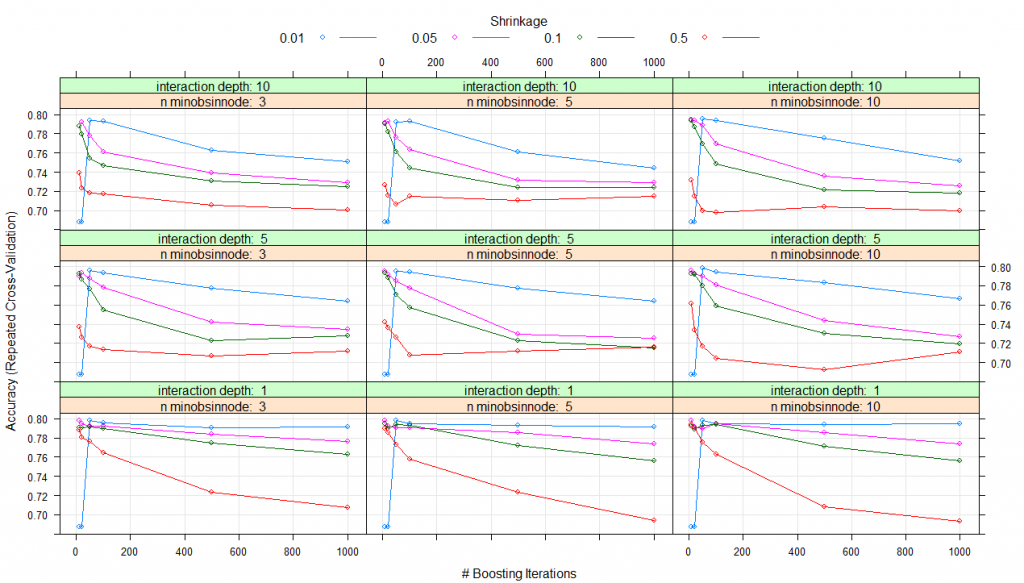
modelLookup(model='gbm') #model         parameter                   label forReg forClass probModel #1   gbm           n.trees   # Boosting Iterations   TRUE     TRUE      TRUE #2   gbm interaction.depth          Max Tree Depth   TRUE     TRUE      TRUE #3   gbm         shrinkage               Shrinkage   TRUE     TRUE      TRUE #4   gbm    n.minobsinnode Min. Terminal Node Size   TRUE     TRUE      TRUE #using grid search #Creating grid grid <- expand.grid(n.trees=c(10,20,50,100,500,1000),shrinkage=c(0.01,0.05,0.1,0.5),n.minobsinnode = c(3,5,10),interaction.depth=c(1,5,10)) # training the model model_gbm<-train(trainSet[,predictors],trainSet[,outcomeName],method='gbm',trControl=fitControl,tuneGrid=grid) # summarizing the model print(model_gbm) #Stochastic Gradient Boosting #461 samples #5 predictor #2 classes: '0', '1' #No pre-processing #Resampling: Cross-Validated (5 fold, repeated 5 times) #Summary of sample sizes: 368, 370, 369, 369, 368, 369, ... #Resampling results across tuning parameters: #  shrinkage  interaction.depth  n.minobsinnode  n.trees  Accuracy   Kappa    #0.01        1                  3                10     0.6876416  0.0000000 #0.01        1                  3                20     0.6876416  0.0000000 #0.01        1                  3                50     0.7982345  0.4423609 #0.01        1                  3               100     0.7952190  0.4364383 #0.01        1                  3               500     0.7904882  0.4342300 #0.01        1                  3              1000     0.7913627  0.4421230 #0.01        1                  5                10     0.6876416  0.0000000 #0.01        1                  5                20     0.6876416  0.0000000 #0.01        1                  5                50     0.7982345  0.4423609 #0.01        1                  5               100     0.7943635  0.4351912 #0.01        1                  5               500     0.7930783  0.4411348 #0.01        1                  5              1000     0.7913720  0.4417463 #0.01        1                 10                10     0.6876416  0.0000000 #0.01        1                 10                20     0.6876416  0.0000000 #0.01        1                 10                50     0.7982345  0.4423609 #0.01        1                 10               100     0.7943635  0.4351912 #0.01        1                 10               500     0.7939525  0.4426503 #0.01        1                 10              1000     0.7948362  0.4476742 #0.01        5                  3                10     0.6876416  0.0000000 #0.01        5                  3                20     0.6876416  0.0000000 #0.01        5                  3                50     0.7960556  0.4349571 #0.01        5                  3               100     0.7934987  0.4345481 #0.01        5                  3               500     0.7775055  0.4147204 #... #0.50        5                 10               100     0.7045617  0.2834696 #0.50        5                 10               500     0.6924480  0.2650477 #0.50        5                 10              1000     0.7115234  0.3050953 #0.50       10                  3                10     0.7389117  0.3681917 #0.50       10                  3                20     0.7228519  0.3317001 #0.50       10                  3                50     0.7180833  0.3159445 #0.50       10                  3               100     0.7172417  0.3189655 #0.50       10                  3               500     0.7058472  0.3098146 #0.50       10                  3              1000     0.7001852  0.2967784 #0.50       10                  5                10     0.7266895  0.3378430 #0.50       10                  5                20     0.7154746  0.3197905 #0.50       10                  5                50     0.7063535  0.2984819 #0.50       10                  5               100     0.7151012  0.3141440 #0.50       10                  5               500     0.7108516  0.3146822 #0.50       10                  5              1000     0.7147320  0.3225373 #0.50       10                 10                10     0.7314871  0.3327504 #0.50       10                 10                20     0.7150814  0.3081869 #0.50       10                 10                50     0.6993723  0.2815981 #0.50       10                 10               100     0.6977416  0.2719140 #0.50       10                 10               500     0.7037864  0.2854748 #0.50       10                 10              1000     0.6995610  0.2869718

Accuracy was used to select the optimal model using  the largest value.

The final values used for the model were n.trees = 10, interaction.depth = 1, shrinkage = 0.05 and n.minobsinnode = 3

plot(model_gbm)

caret-1

Thus, for all the parameter combinations that you listed in expand.grid(), a model will be created and tested using cross-validation. The set of parameters with the best cross-validation performance will be used to create the final model which you get at the end.

 

6.2. Using tuneLength

Instead, of specifying the exact values for each parameter for tuning we can simply ask it to use any number of possible values for each tuning parameter through tuneLength. Let’s try an example using tuneLength=10.

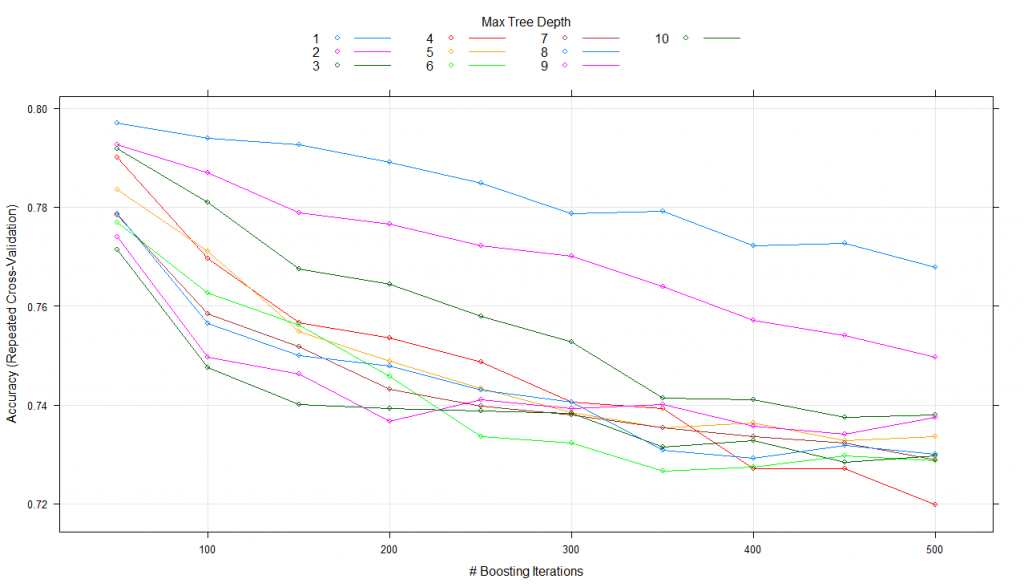
#using tune length model_gbm<-train(trainSet[,predictors],trainSet[,outcomeName],method='gbm',trControl=fitControl,tuneLength=10) print(model_gbm) #Stochastic Gradient Boosting #461 samples #5 predictor #2 classes: '0', '1' #No pre-processing #Resampling: Cross-Validated (5 fold, repeated 5 times) #Summary of sample sizes: 368, 369, 369, 370, 368, 369, ... #Resampling results across tuning parameters: #  interaction.depth  n.trees  Accuracy   Kappa    #1                  50      0.7978084  0.4541008 #1                 100      0.7978177  0.4566764 #1                 150      0.7934792  0.4472347 #1                 200      0.7904310  0.4424091 #1                 250      0.7869714  0.4342797 #1                 300      0.7830488  0.4262414 ... #10                 100      0.7575230  0.3860319 #10                 150      0.7479757  0.3719707 #10                 200      0.7397290  0.3566972 #10                 250      0.7397285  0.3561990 #10                 300      0.7362552  0.3513413 #10                 350      0.7340812  0.3453415 #10                 400      0.7336416  0.3453117 #10                 450      0.7306027  0.3415153 #10                 500      0.7253854  0.3295929

Tuning parameter ‘shrinkage’ was held constant at a value of 0.1

Tuning parameter ‘n.minobsinnode’ was held constant at a value of 10

Accuracy was used to select the optimal model using  the largest value.

The final values used for the model were n.trees = 50, interaction.depth = 2, shrinkage = 0.1 and n.minobsinnode = 10.

plot(model_gbm)

caret-2

Here, it keeps the shrinkage and n.minobsinnode parameters constant while alters n.trees and interaction.depth over 10 values and uses the best combination to train the final model with.

 

7. Variable importance estimation using caret

Caret also makes the variable importance estimates accessible with the use of varImp() for any model. Let’s have a look at the variable importance for all the four models that we created:

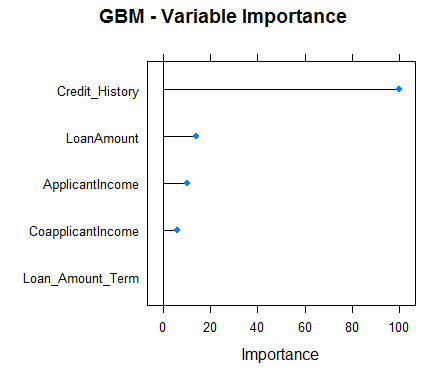
#Checking variable importance for GBM #Variable Importance varImp(object=model_gbm) #gbm variable importance #Overall #Credit_History    100.000 #LoanAmount         16.633 #ApplicantIncome     7.104 #CoapplicantIncome   6.773 #Loan_Amount_Term    0.000 #Plotting Varianle importance for GBM plot(varImp(object=model_gbm),main="GBM - Variable Importance")

caret-3

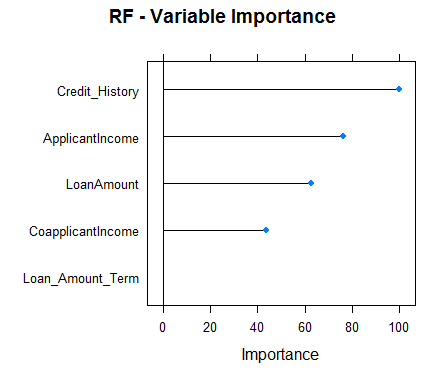
#Checking variable importance for RF varImp(object=model_rf) #rf variable importance #Overall #Credit_History     100.00 #ApplicantIncome     73.46 #LoanAmount          60.59 #CoapplicantIncome   40.43 #Loan_Amount_Term     0.00 #Plotting Varianle importance for Random Forest plot(varImp(object=model_rf),main="RF - Variable Importance")

caret-8

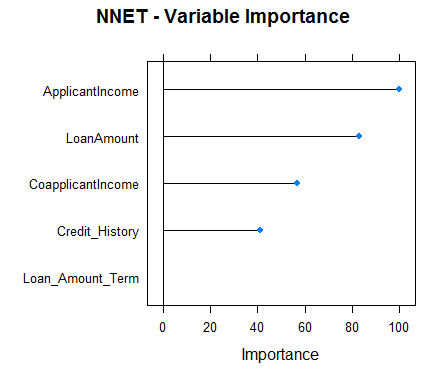
#Checking variable importance for NNET varImp(object=model_nnet) #nnet variable importance #Overall #ApplicantIncome    100.00 #LoanAmount          82.87 #CoapplicantIncome   56.92 #Credit_History      41.11 #Loan_Amount_Term     0.00 #Plotting Variable importance for Neural Network plot(varImp(object=model_nnet),main="NNET - Variable Importance")

caret-4

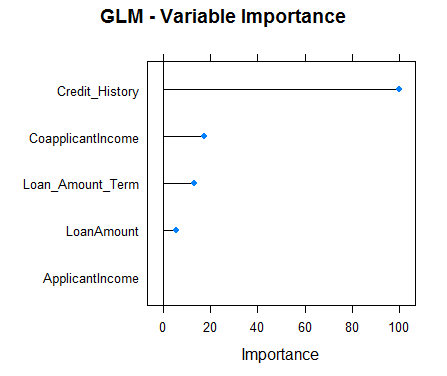
#Checking variable importance for GLM varImp(object=model_glm) #glm variable importance #Overall #Credit_History    100.000 #CoapplicantIncome  17.218 #Loan_Amount_Term   12.988 #LoanAmount          5.632 #ApplicantIncome     0.000 #Plotting Variable importance for GLM plot(varImp(object=model_glm),main="GLM - Variable Importance")

caret-5

Clearly, the variable importance estimates of different models differs and thus might be used to get a more holistic view of importance of each predictor. Two main uses of variable importance from various models are:

  • Predictors that are important for the majority of models represents genuinely important predictors.
  • Foe ensembling, we should use predictions from models that have significantly different variable importance as their predictions are also expected to be different. Although, one thing that must be make sure is that all of them are sufficiently accurate.

 

8. Predictions using Caret

For predicting the dependent variable for the testing set, Caret offers predict.train(). You need to specify the model name, testing data. For classification problems, Caret also offers another feature named type which can be set to either “prob” or “raw”. For type=”raw”, the predictions will just be the outcome classes for the testing data while for type=”prob”, it will give probabilities for the occurrence of each observation in various classes of the outcome variable.

Let’s take a look at the predictions from our GBM model:

#Predictions predictions<-predict.train(object=model_gbm,testSet[,predictors],type="raw") table(predictions) #predictions #0   1 #28 125

Caret also provides a confusionMatrix function which will give the confusion matrix along with various other metrics for your predictions. Here is the performance analysis of our GBM model:

confusionMatrix(predictions,testSet[,outcomeName]) #Confusion Matrix and Statistics #Reference #Prediction   0   1 #0  25   3 #1  23 102 #Accuracy : 0.8301         #95% CI : (0.761, 0.8859) #No Information Rate : 0.6863         #P-Value [Acc > NIR] : 4.049e-05      #Kappa : 0.555          #Mcnemar's Test P-Value : 0.0001944      #Sensitivity : 0.5208         #Specificity : 0.9714         #Pos Pred Value : 0.8929 #Neg Pred Value : 0.8160         #Prevalence : 0.3137         #Detection Rate : 0.1634         #Detection Prevalence : 0.1830         #Balanced Accuracy : 0.7461         #'Positive' Class : 0

Additional Resources

 

End Notes

Caret is one of the most powerful and useful packages ever made in R. It alone has the capability to fulfill all the needs for predictive modeling from preprocessing to interpretation. Additionally, its syntax is also very easy to use. If you use R, I’ll encourage you to use Caret.

Caret is a very comprehensive package and instead of covering all the functionalities that it offers, I thought it’ll be a better idea to show an end-to-end implementation of Caret on a real hackathon J dataset. I have tried to cover as many functions in Caret as I could, but Caret has a lot more to offer. For going in depth, you might find the resources mentioned above very useful. Several of these resources have been written by Max Kuhn (the creator of caret package) himself.

You can test your skills and knowledge. Check out Live Competitions and compete with best Data Scientists from all over the world.package in the comments below.

caretCaret in Rcaret packagedata splittingfeature selectionparameter tuningprediction using caretRVariable Importance
saurav kaushik
saurav kaushik

Saurav is a Data Science enthusiast, currently in the final year of his graduation at MAIT, New Delhi. He loves to use machine learning and analytics to solve complex data problems.

Free Courses

Generative AI 4.7

Generative AI - A Way of Life

Explore Generative AI for beginners: create text and images, use top AI tools, learn practical skills, and ethics.
Large Language Models 4.5

Getting Started with Large Language Models

Master Large Language Models (LLMs) with this course, offering clear guidance in NLP and model training made simple.
Prompt Engineering 4.6

Building LLM Applications using Prompt Engineering

This free course guides you on building LLM apps, mastering prompt engineering, and developing chatbots with enterprise data.
LlamaIndex 4.8

Improving Real World RAG Systems: Key Challenges & Practical Solutions

Explore practical solutions, advanced retrieval strategies, and agentic RAG systems to improve context, relevance, and accuracy in AI-driven applications.
RAG systems using LlamaIndex 4.7

Microsoft Excel: Formulas & Functions

Master MS Excel for data analysis with key formulas, functions, and LookUp tools in this comprehensive course.

Recommended Articles

Responses From Readers

Clear

KISHORE
KISHORE

Hello @Saurav Kaushik , I really appreciate you for sharing such a nice article on CART. This really help a lot !

123

Saurav Kaushik
Saurav Kaushik

Hey Kishore. Glad you liked it. Happy to help!

123
zhanyou Xu
zhanyou Xu

where can I download the data used in this article? thank you. zhanyou

123

Saurav Kaushik
Saurav Kaushik

Hey Zhanyou. The dataset used is from a practice problem and can be accessed at: https://datahack.analyticsvidhya.com/contest/practice-problem-loan-prediction-iii/

123
Miguel Hidalgo
Miguel Hidalgo

Hi Saurav, how are you, nice article!. Saurav, where can I download the data file? train_u6lujuX_CVtuZ9i.csv Thanks, Miguel

123

Saurav Kaushik
Saurav Kaushik

Hey Miguel. Thanks. You can get the data from the following practice problem: https://datahack.analyticsvidhya.com/contest/practice-problem-loan-prediction-iii/

123

Write for us

Write, captivate, and earn accolades and rewards for your work
  • Reach a Global Audience
  • Get Expert Feedback
  • Build Your Brand & Audience
  • Cash In on Your Knowledge
  • Join a Thriving Community
  • Level Up Your Data Science Game
imag
Congratulations, You Did It!
Well Done on Completing Your Learning Journey. Stay curious and keep exploring!
The “caret” Package – One stop solution for building predictive models in R
The “caret” Package – One stop solution for building predictive models in R
Beginner’s Guide To Text Classification Using PyCaret
Beginner’s Guide To Text Classification Using PyCaret

We use cookies essential for this site to function well. Please click to help us improve its usefulness with additional cookies. Learn about our use of cookies in our Privacy Policy & Cookies Policy.

Show details