Introduction
Whether you are a novice at data science or a veteran with Deep Learning Course certification, Deep learning is hard to ignore. And it deserves attention, as deep learning is helping us achieve the AI dream of getting near-human performance in everyday tasks.
Given the importance to learn Deep learning for a data scientist, we created a skill test to help people assess themselves on Deep Learning Questions. A total of 644 people registered for this skill test.
If you are one of those who missed out on this skill test, here are the questions and solutions. You missed the real-time test but can read this article to find out how many could have answered correctly.
Here is the leaderboard for the participants who took the test for 30 Deep Learning Questions. If you are just getting started with Deep Learning, here is a course to assist you in your journey to Master Deep Learning:
Overall Distribution
Below is the distribution of the scores of the participants:
You can access the scores here. More than 200 people participated in the skill test and the highest score obtained was 26. Interestingly, the distribution of scores ended up being very similar to the past 2 tests:
Clearly, a lot of people start the test without understanding Deep Learning, which is not the case with other skill tests. This also means that these solutions would be useful to a lot of people.
Helpful Resources on Deep Learning
Here are some resources to get in-depth knowledge of the subject.
- Fundamentals of Deep Learning – Starting with Artificial Neural Network
- Understanding and Coding Neural Network from Scratch
- Practical Guide to implementing Neural Networks in Python (using Theano)
- A Complete Guide on Getting Started with Deep Learning in Python
- Tutorial: Optimizing Neural Networks using Keras (with Image recognition case study)
- An Introduction to Implementing Neural Networks using TensorFlow
Skill test Deep Learning Questions and Answers
1) Is the data linearly separable?

A) Yes
B) No
Solution: B
If you can draw a line or plane between the data points, it is said to be linearly separable.
2) Which of the following are universal approximators?
A) Kernel SVM
B) Neural Networks
C) Boosted Decision Trees
D) All of the above
Solution: DAll of the above methods can approximate any function.
3) In which of the following applications can we use deep learning to solve the problem?
A) Protein structure prediction
B) Prediction of chemical reactions
C) Detection of exotic particles
D) All of these
Solution: DWe can use a neural network to approximate any function so it can theoretically be used to solve any problem.
4) Which of the following statements is true when you use 1×1 convolutions in a CNN?
A) It can help in dimensionality reduction
B) It can be used for feature pooling
C) It suffers less overfitting due to small kernel size
D) All of the above
Solution: D1×1 convolutions are called bottleneck structure in CNN.
5) Question Context:
Statement 1: It is possible to train a network well by initializing all the weights as 0
Statement 2: It is possible to train a network well by initializing biases as 0
Which of the statements given above is true?
A) Statement 1 is true while Statement 2 is false
B) Statement 2 is true while statement 1 is false
C) Both statements are true
D) Both statements are false
Solution: BEven if all the biases are zero, there is a chance that neural network may learn. On the other hand, if all the weights are zero; the neural neural network may never learn to perform the task.
6) The number of nodes in the input layer is 10 and the hidden layer is 5. The maximum number of connections from the input layer to the hidden layer are
A) 50
B) Less than 50
C) More than 50
D) It is an arbitrary value
Solution: A
Since MLP is a fully connected directed graph, the number of connections are a multiple of number of nodes in input layer and hidden layer.
7) The input image has been converted into a matrix of size 28 X 28 and a kernel/filter of size 7 X 7 with a stride of 1. What will be the size of the convoluted matrix?
A) 22 X 22
B) 21 X 21
C) 28 X 28
D) 7 X 7
Solution: A
The size of the convoluted matrix is given by C=((I-F+2P)/S)+1, where C is the size of the Convoluted matrix, I is the size of the input matrix, F the size of the filter matrix and P the padding applied to the input matrix. Here P=0, I=28, F=7 and S=1. There the answer is 22.
8) In a simple MLP model with 8 neurons in the input layer, 5 neurons in the hidden layer and 1 neuron in the output layer. What is the size of the weight matrices between hidden output layer and input hidden layer?
A) [1 X 5] , [5 X 8]
B) [8 X 5] , [ 1 X 5]
C) [8 X 5] , [5 X 1]
D) [5 x 1] , [8 X 5]
Solution: D
The size of weights between any layer 1 and layer 2 Is given by [nodes in layer 1 X nodes in layer 2]
9) Given below is an input matrix named I, kernel F and Convoluted matrix named C. Which of the following is the correct option for matrix C with stride =2 ?

A)

B)
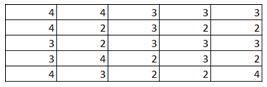
C)

D)

Solution: C
1 and 2 are automatically eliminated since they do not conform to the output size for a stride of 2. Upon calculation option 3 is the correct answer.
10) Given below is an input matrix of shape 7 X 7. What will be the output on applying a max pooling of size 3 X 3 with a stride of 2?

A)

B)

C)

D)
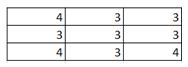
Solution: A
Max pooling takes a 3 X 3 matrix and takes the maximum of the matrix as the output. Slide it over the entire input matrix with a stride of 2 and you will get option (1) as the answer.
11) Which of the following functions can be used as an activation function in the output layer if we wish to predict the probabilities of n classes (p1, p2..pk) such that sum of p over all n equals to 1?
A) Softmax
B) ReLu
C) Sigmoid
D) Tanh
Solution: A
Softmax function is of the form in which the sum of probabilities over all k sum to 1.
12) Assume a simple MLP model with 3 neurons and inputs= 1,2,3. The weights to the input neurons are 4,5 and 6 respectively. Assume the activation function is a linear constant value of 3. What will be the output ?
A) 32
B) 643
C) 96
D) 48
Solution: C
The output will be calculated as 3(1*4+2*5+6*3) = 96
13) Which of following activation function can’t be used at output layer to classify an image ?
A) sigmoid
B) Tanh
C) ReLU
D) If(x>5,1,0)
E) None of the above
Solution: C
ReLU gives continuous output in range 0 to infinity. But in output layer, we want a finite range of values. So option C is correct.
14) [True | False] In the neural network, every parameter can have their different learning rate.
A) TRUE
B) FALSE
Solution: A
Yes, we can define the learning rate for each parameter and it can be different from other parameters.
15) Dropout can be applied at visible layer of Neural Network model?
A) TRUE
B) FALSE
Solution: A
Look at the below model architecture, we have added a new Dropout layer between the input (or visible layer) and the first hidden layer. The dropout rate is set to 20%, meaning one in 5 inputs will be randomly excluded from each update cycle.
def create_model(): # create model model = Sequential() model.add(Dropout(0.2, input_shape=(60,))) model.add(Dense(60, activation='relu')) model.add(Dense(1, activation='sigmoid')) # Compile model sgd = SGD(lr=0.1) model.compile(loss='binary_crossentropy', optimizer=sgd, metrics=['accuracy']) return model
16) I am working with the fully connected architecture having one hidden layer with 3 neurons and one output neuron to solve a binary classification challenge. Below is the structure of input and output:
Input dataset: [ [1,0,1,0] , [1,0,1,1] , [0,1,0,1] ]
Output: [ [1] , [1] , [0] ]
To train the model, I have initialized all weights for hidden and output layer with 1.
What do you say model will able to learn the pattern in the data?
A) Yes
B) No
Solution: B
As all the weights of the neural network model are same, so all the neurons will try to do the same thing and the model will never converge.
17) Which of the following neural network training challenge can be solved using batch normalization?
A) Overfitting
B) Restrict activations to become too high or low
C) Training is too slow
D) Both B and C
E) All of the above
Solution: D
Batch normalization restricts the activations and indirectly improves training time.
18) Which of the following would have a constant input in each epoch of training a Deep Learning model?
A) Weight between input and hidden layer
B) Weight between hidden and output layer
C) Biases of all hidden layer neurons
D) Activation function of output layer
E) None of the above
Solution: A
Weights between input and hidden layer are constant.
19) True/False: Changing Sigmoid activation to ReLu will help to get over the vanishing gradient issue?
A) TRUE
B) FALSE
Solution: A
ReLU can help in solving vanishing gradient problem.
20) In CNN, having max pooling always decrease the parameters?
A) TRUE
B) FALSE
Solution: B
This is not always true. If we have a max pooling layer of pooling size as 1, the parameters would remain the same.
21) [True or False] BackPropogation cannot be applied when using pooling layers
A) TRUE
B) FALSE
Solution: B
BackPropogation can be applied on pooling layers too.
22) What value would be in place of question mark?

A) 3
B) 4
C) 5
D) 6
Solution: B
Option B is correct
23) For a binary classification problem, which of the following architecture would you choose?
A) 1
B) 2
C) Any one of these
D) None of these
Solution: C
We can either use one neuron as output for binary classification problem or two separate neurons.
24) Suppose there is an issue while training a neural network. The training loss/validation loss remains constant. What could be the possible reason?
A) Architecture is not defined correctly
B) Data given to the model is noisy
C) Both of these
Solution: C
Both architecture and data could be incorrect. Refer this article https://www.analyticsvidhya.com/blog/2017/07/debugging-neural-network-with-tensorboard/
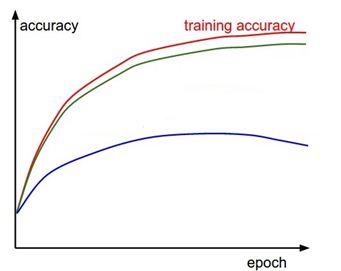
25)
The red curve above denotes training accuracy with respect to each epoch in a deep learning algorithm. Both the green and blue curves denote validation accuracy.
Which of these indicate overfitting?
A) Green Curve
B) Blue Curve
Solution: B
Blue curve shows overfitting, whereas green curve is generalized.
26) Which of the following statement is true regrading dropout?
1: Dropout gives a way to approximate by combining many different architectures
2: Dropout demands high learning rates
3: Dropout can help preventing overfitting
A) Both 1 and 2
B) Both 1 and 3
C) Both 2 and 3
D) All 1, 2 and 3
Solution: B
Statements 1 and 3 are correct, statement 2 is not always true. Even after applying dropout and with low learning rate, a neural network can learn.
27) Gated Recurrent units can help prevent vanishing gradient problem in RNN.
A) True
B) False
Solution: A
Option A is correct. This is because it has implicit memory to remember past behavior.
28) Suppose you are using early stopping mechanism with patience as 2, at which point will the neural network model stop training?
| Sr. No. | Training Loss | Validation Loss |
| 1 | 1.0 | 1.1 |
| 2 | 0.9 | 1.0 |
| 3 | 0.8 | 1.0 |
| 4 | 0.7 | 1.0 |
| 5 | 0.6 | 1.1 |
A) 2
B) 3
C) 4
D) 5
Solution: C
As we have set patience as 2, the network will automatically stop training after epoch 4.
29) [True or False] Sentiment analysis using Deep Learning is a many-to one prediction task
A) TRUE
B) FALSE
Solution: A
Option A is correct. This is because from a sequence of words, you have to predict whether the sentiment was positive or negative.
30) What steps can we take to prevent overfitting in a Neural Network?
A) Data Augmentation
B) Weight Sharing
C) Early Stopping
D) Dropout
E) All of the above
Solution: E
All of the above mentioned methods can help in preventing overfitting problem.
End Notes
I tried my best to make the solutions to deep learning questions as comprehensive as possible but if you have any doubts please drop in your comments below. I would love to hear your feedback about the skill test. For more such skill tests, check out our current hackathons.








Really Good blog post about skill test deep learning. provided a helpful information.I hope that you will post more updates like this.
Thanks Shalini
Question 18: The explanation for question 18 is incorrect: "Weights between input and hidden layer are constant." The weights are not constant but rather the input to the neurons at input layer is constant. Tests like this should be more mindful in terminology: the weights themselves do not have "input", but rather the neurons that do. Question 20: while this question is technically valid, it should not appear in future tests. Since 1x1 max pooling operation is equivalent to making a copy of the previous layer it does not have any practical value. The sensible answer would have been A) TRUE. Could you elaborate a scenario that 1x1 max pooling is actually useful?
Hi, Thanks for the feedback! Q18: Consider this, whenever we depict a neural network; we say that the input layer too has neurons. Also its true that each neuron has its own weights and biases. So to represent this concept in code, what we do is, we define an input layer which has the sole purpose as a "pass through" layer which takes the input and passes it to the next layer. Now when we backpropogate through the network, we ignore this input layer weights and update the rest of the network. So the question depicts this scenario. Q20. The question was intended as a twist so that the participant would expect every scenario in which a neural network can be created. But you are correct that a 1x1 pooling layer would not have any practical value.
In question 3 the explanation is similar to question 2 and does not address the question subject.
Hi, I have updated the statement a bit