Learn How to Perform Feature Extraction from Graphs using DeepWalk

Overview

• Extracting features from tabular or image data is a well-known concept – but what about graph data?
• Learn how to extract features from a graph using DeepWalk, a robust and scalable method
• We will also implement DeepWalk in Python to find similar Wikipedia pages

Introduction

I’m enthralled by how Google Search works. There are so many little nuggets that come up each time I search for a topic. Take the amazing “People also search for”? example. When I search for a specific personality or a book, I always get similar suggestions from Google.

For instance, when I search for “Lewis Hamilton”, I get a list of other prominent Formula 1 drivers:

This rich and relevant content is served by highly sophisticated algorithms working on graph data. It is this power of graphs and networks that keeps me (and so many other data scientists) captivated! There are so many new avenues that have opened up since I’ve started working with graphs.

In this article, I will walk through one of the most important steps in any machine learning project – Feature Extraction. There’s a slight twist here, though. We will extract features from a graph dataset and use these features to find similar nodes (entities).

I recommend going through the below articles to get a hang of what graphs are and how they work:

• Introduction to Graph Theory and its Applications using Python
• Knowledge Graph – A Powerful Data Science Technique to Mine Information from Text

Table of Contents

1. Graph-Representation of Data
2. Different Types of Graph-based Features
   • Node Attributes
   • Local Structural Features
   • Node Embeddings
3. Introduction to DeepWalk
4. Implement DeepWalk in Python to find similar Wikipedia Pages

Graph-Representation of Data

What comes to your mind when you think about “Networks”? It’s typically things like social networks, the internet, connected IoT devices, rail networks, or telecom networks. In Graph theory, these networks are called graphs.

Basically, a network is a collection of interconnected nodes. The nodes represent entities and the connections between them are some sort of relationships.

For example, we can represent a set of social media accounts in the form of a graph:

The nodes are the digital profile of the users, and the connections represent the relationships among them, such as who follows whom or who is friends with whom. 

And the use cases of graphs aren’t just limited to social media! We can represent other kinds of data as well with graphs and networks (and we will cover a unique industry use case in this article).

Why should we represent Data as Graphs?

I can see you wondering – why not just visualize your data using typical data visualization techniques? Why introduce complexity and learn a new concept? Well, let’s see.

Graph datasets and databases help us address several challenges we face while dealing with structured data. That’s the reason why today’s major tech companies, such as Google, Uber, Amazon, and Facebook use graphs in some form or another.

Let’s take an example to understand why a graph is an important representation of data. Take a look at the figure below:

This is a small dataset of a few Facebook users (A, B, C, D, E, F, and G). The left half of the image contains the tabular form of this data. Each row represents a user and one of his/her friends.

The right half contains a graph representing the same set of users. The edges of this graph tell us that the connected nodes are friends on Facebook. Now, let’s solve a simple query:

“Find the friends and friends-of-friends of user A.”

Look at both the tabular data and the graph above. Which data form is more suitable to answer such a query?

It is much easier to use the graph form to solve that problem because we just have to traverse the originating paths (A-B-C and A-D-F) from node A to the length of 2 to find the friends and friends-of-friends.

Hence, graphs can easily capture relationships among the nodes which is quite a difficult task in a conventional data structure. Starting to see their importance in the grand scheme of things? So now let’s see what kind of problems we can solve using graphs.

Different Types of Graph-based Features

To solve the problems mentioned above, we cannot feed the graph directly to a machine learning model. We have to first create features from it which would then be used by the model.

This process is similar to what we do in Natural Language Processing (NLP) or Computer Vision. We first extract the numerical features from the text or images and then give those features as input to a machine learning model:

The features extracted from a graph can be broadly divided into three categories:

1. Node Attributes: We know that the nodes in a graph represent entities and these entities have their own characteristic attributes. We can use these attributes as features for each and every node. For example, in an airline route network, the nodes would represent the airports. These nodes would have features like aircraft capacity, number of terminals, landing area, etc.
2. Local Structural Features: Node features like degree (count of adjacent nodes), mean of degrees of neighbor nodes, number of triangles a node forms with other nodes, etc.
3. Node Embeddings: The above-discussed features carry only node related information. They do not capture the information about the context of a node. By context, I mean the surrounding nodes. Node embeddings address this issue to a certain extent by representing every node by a fixed-length vector. These vectors are able to capture information about the surrounding nodes (contextual information)

Two important modern-day algorithms for learning node embeddings are DeepWalk and Node2Vec. In this article, we will cover and implement the DeepWalk algorithm.

Introduction to DeepWalk

To understand DeepWalk, it is important to have a proper understanding of word embeddings, and how they are used in NLP. I recommend going through the explanation of Word2Vec, a popular word embedding, in the article below:

• Building a Recommendation System using Word2vec

To put things into context, word embeddings are the vector representation of text and they capture the contextual information. Let’s look at the sentences below:

• I took a bus to Mumbai
• I took a train to Mumbai

The vectors of the words in bold (bus and train) would be quite similar because they appear in the same context, i.e. the words before and after the bold text. This information is of great use for many NLP tasks, such as text classification, named entity recognition, language modeling, machine translation and many more.

We can capture this sort of contextual information in graphs as well, for every node. However, to learn word embeddings in the NLP space, we feed sentences to a Skip-gram model (a shallow neural network). A sentence is a sequence of words in a certain order.

So, to obtain node embeddings, we first need to arrange for sequences of nodes from the graph. How do we get these sequences from a graph? Well, there is a technique for this task called Random Walk.

What is Random Walk?

Random Walk is a technique to extract sequences from a graph. We can use these sequences to train a skip-gram model to learn node embeddings.

Let me illustrate how Random Walk works. Let’s consider the undirected graph below:

We will apply Random Walk on this graph and extract sequences of nodes from it. We will start from Node 1 and cover two edges in any direction:

From node 1, we could have gone to any connected node (node 3 or node 4). We randomly selected node 4. Now again from node 4, we have to randomly choose our way forward. We’ll go with node 5. Now we have a sequence of 3 nodes: [node 1 – node 4 – node 5].

Let’s generate another sequence, but this time from a different node:

Let’s select node 15 as the originating node. From nodes 5 and 6, we will randomly select node 6. Then from nodes 11 and 2, we select node 2. The new sequence is [node 15 – node 6 – node 2].

We will repeat this process for every node in the graph. This is how the Random Walk technique works.

After generating node-sequences, we have to feed them to a skip-gram model to get node embeddings. That entire process is known as DeepWalk.

In the next section, we will implement DeepWalk from scratch on a network of Wikipedia articles.

Implement DeepWalk to find Similar Wikipedia Pages

This is going to be the most exciting part of the article, especially if you love coding. So fire up those Jupyter Notebooks!

We are going to use a graph of Wikipedia articles and extract node embeddings from it using DeepWalk. Then we will use these embeddings to find similar Wikipedia pages.

We won’t be touching the text inside any of these articles. Our aim is to calculate the similarity between the pages purely on the basis of the structure of the graph.

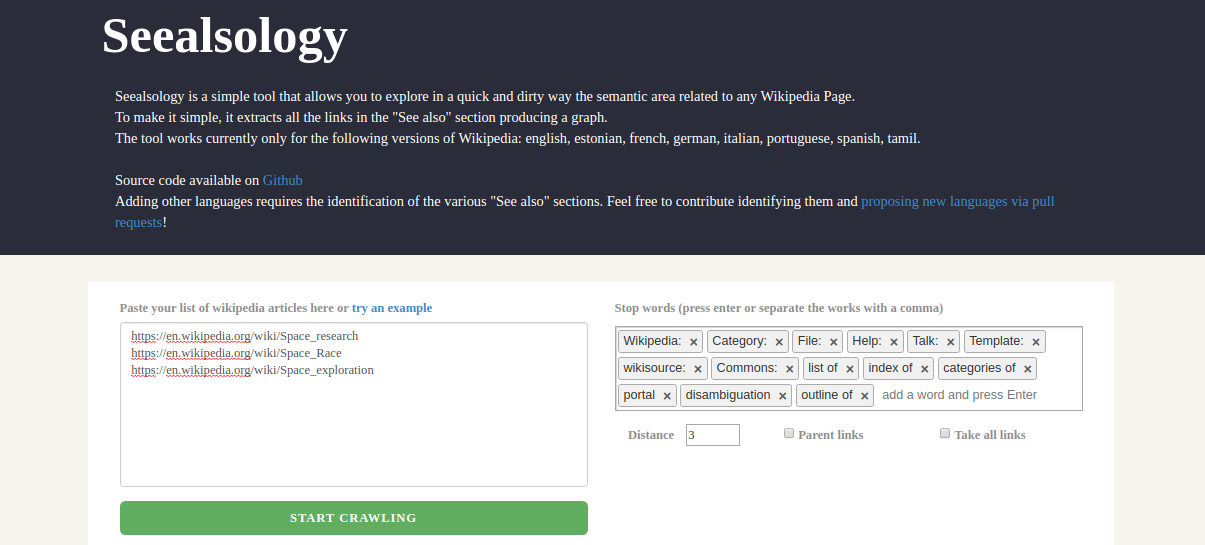
But wait – how and where can we get the Wikipedia graph dataset? That’s where an awesome tool called Seealsology will help us. This helps us create graphs from any Wikipedia page. You can even give multiple Wikipedia pages as the input. Here is a screenshot of the tool:

The nodes of the resultant graph are the Wikipedia pages that have links in the input Wikipedia page(s). So, if a page has a hyperlink on another page, then there would be a link between the two pages in the graph.

Have a look at how this graph is formed at Seealsology. It’s a treat to watch!

The close proximity of the nodes in a graph, such as the one above, does not necessarily mean that they are semantically similar. Hence, there is a need to represent these nodes in a vector space where we can identify similar nodes.

Of course, we can use other methods to do this task. For instance, we can parse all the text in these nodes (Wikipedia pages) and represent each page with a vector with the help of word embeddings. Then, we can compute the similarity between these vectors to find similar pages. However, there are some drawbacks of this NLP-based approach:

• If there are millions of nodes, then we need a huge amount of computational power for parsing the text and learning word embeddings from all these nodes or pages
• This approach will not capture the information lying in the connections between these pages. For example, a pair of directly connected pages might have a stronger relationship than a pair of indirectly connected pages

These shortcomings can easily be handled by the graphs and the node embeddings. So, once your graph is ready, you can download a TSV file from Seealsology. In this file, every row is a pair of nodes. We will use this data to reconstruct the graph and apply the DeepWalk algorithm on it to obtain node embeddings.

Let’s get started! You can use Jupyter Notebook or Colab for this.

Import the Required Python Libraries

Load Dataset

You can download the .tsv file from here.

Output:

Both source and target contain Wikipedia entities. For any row, the entity, in target, has its hyperlink in the Wikipedia page of the entity in the source column.

Construct the Graph

Let’s check the number of nodes in our graph:

len(G)

Output: 2088

There are 2,088 Wikipedia pages we will be working on.

Random Walk

Ready to walk the graph?

Here, I have defined a function that will take a node and length of the path to be traversed as inputs. It will walk through the connected nodes from the specified input node in a random fashion. Finally, it will return the sequence of traversed nodes:

Let’s try out this function for the node “space exploration”:

get_randomwalk('space exploration', 10)

Output: 

Here, I have specified the length to traverse as 10. You can change this number and play around with it. Next, we will capture the random walks for all the nodes in our dataset:

Output: 10,440

So, with the traverse length set to 10, we have got 10,440 random walk sequences of nodes. We can use these sequences as inputs to a skip-gram model and extract the weight learned by the model (which are nothing but the node embeddings).

DeepWalk

Next, we will train the skip-gram model with the random walks:

Now, every node in the graph is represented by a fixed length (100) vector. Let’s find out the most similar pages to “space tourism”:

model.similar_by_word('space tourism')

Output:

Quite interesting! All these pages are related to Civil Space Travel related topics. Feel free to extract similar nodes for other entities.

Now, I want to see how well our node embeddings capture the similarity between different nodes. I have handpicked a few nodes from the graph and will plot them on a 2-dimensional space:

Below I have defined a function that will plot the vectors of the selected nodes in a 2-dimensional space:

Let’s plot the selected nodes:

plot_nodes(terms)

Output:

Looks good! As you can see, similar Wikipedia entities are grouped together. For example, “soviet moonshot”, “soyuz 7k-l1”, “moon landing”, and “lunar escape systems” are all attempts made to land on the moon.

This is why DeepWalk embeddings are so useful. We can use these embeddings to solve multiple graph-related problems such as link prediction, node classification, question-answering system and many more.

Feel free to execute the code below. It will generate Random Walk sequences and fetch similar nodes using DeepWalk for an input node.

End Notes

I really enjoyed exploring DeepWalk for graph data in this article, and I can’t wait to get my hands dirty with other graph algorithms. Watch this space for more in the coming weeks!

I encourage you to implement this code, play around with it, and build your own graph model. It’s the best way to learn any concept. Full code is available here.

Have you worked with graphs in data science before? I would love to connect with you and discuss this.

References

• DeepWalk: Online Learning of Social Representations

Prateek joshi

Data Scientist at Analytics Vidhya with multidisciplinary academic background. Experienced in machine learning, NLP, graphs & networks. Passionate about learning and applying data science to solve real world problems.