Artificial Neural Networks are computing systems that are inspired by the working of the Human Neuron. It is the backbone of Deep Learning that led to the achievement of bigger milestones in almost all the fields thereby bringing an evolution in which we approach a problem. Therefore, it becomes necessary for every aspiring Data Scientist and Machine Learning Engineer to have a good knowledge of these Neural Networks.
In this article, we will discuss the most important questions on the Artificial Neural Networks (ANNs) which is helpful to get you a clear understanding of the techniques, and also for Data Science Interviews, which covers its very fundamental level to complex concepts.
This article was published as a part of the Data Science Blogathon
1. What do you mean by Perceptron?
A perceptron also called an artificial neuron is a neural network unit that does certain computations to detect features.
It is a single-layer neural network used as a linear classifier while working with a set of input data. Since the perceptron uses labeled data points, it functions as a supervised learning algorithm. This algorithm enables neurons to learn and process elements in the training set one at a time.

Image Source: Google Images
2. What are the different types of Perceptrons?
There are two types of perceptrons:
1. Single-Layer Perceptrons– Single-layer perceptrons can learn only linearly separable patterns.
2. Multilayer Perceptrons– Multilayer perceptrons, also known as feedforward neural networks having two or more layers have a higher processing power.
3. What is the use of the Loss functions?
The loss function measures accuracy to identify whether our neural network has learned the patterns accurately using the training data.
This is completed by comparing the training data with the testing data.
Therefore, we consider the loss function a primary measure of the neural network’s performance. In Deep Learning, a good-performing neural network will have a low value of the loss function at all times when training happens.
4. What is the role of the Activation functions in Neural Networks?
The reason for using activation functions in Neural Networks are as follows:
- The idea behind the activation function is to introduce nonlinearity into the neural network so that it can learn more complex functions.
- Without the Activation function, the neural network behaves as a linear classifier, learning the function which is a linear combination of its input data.
- The activation function converts the inputs into outputs.
- The activation function decides whether a neuron should activate, or fire, or not.
- To make the decision, firstly it calculates the weighted sum and further adds bias with it.
- So, the basic purpose of the activation function is to introduce non-linearity into the output of a neuron.
5. List down the names of some popular Activation Functions used in Neural Networks.
Some of the popular activation functions that are used while building the deep learning models are as follows:
- Sigmoid function
- Hyperbolic tangent function
- Rectified linear unit (RELU) function
- Leaky RELU function
- Maxout function
- Exponential Linear unit (ELU) function

6. What do you mean by Cost Function?
While building deep learning models, our whole objective is to minimize the cost function.
A cost function explains how well the neural network is performing for its given training data and the expected output.
It may depend on the neural network parameters such as weights and biases. As a whole, it provides the performance of a neural network.
7. What do you mean by Backpropagation?
The backpropagation algorithm is used to train multilayer perceptrons. It propagates the error information from the end of the network to all the weights inside the network. It allows the efficient computation of the gradient or derivatives.
Backpropagation can be divided into the following steps:
- It can forward the propagation of training data through the network to generate output.
- It uses target value and output value to compute error derivatives by concerning the output activations.
- It can backpropagate to calculate the derivatives of the error concerning output activations in the previous layer and continue for all the hidden layers.
- It uses the previously computed derivatives for output and all hidden layers to calculate the error derivative concerning weights.
- It updates the weights and repeats until the cost function is minimized.
8. How to initialize Weights and Biases in Neural Networks?
Neural network initialization means initialized the values of the parameters i.e, weights and biases. Biases can be initialized to zero but we can’t initialize weights with zero.
Weight initialization is one of the crucial factors in neural networks since bad weight initialization can prevent a neural network from learning the patterns.
On the contrary, a good weight initialization helps in giving a quicker convergence to the global minimum. As a rule of thumb, the rule for initializing the weights is to be close to zero without being too small.
9. Why is zero initialization of weight, not a good initialization technique?
If we initialize the set of weights in the neural network as zero, then all the neurons at each layer will start producing the same output and the same gradients during backpropagation.
As a result, the neural network cannot learn anything at all because there is no source of asymmetry between different neurons. Therefore, we add randomness while initializing the weight in neural networks.
10. Explain Gradient Descent and its types.
Gradient Descent is an optimization algorithm that aims to minimize the cost function or to minimize an error. Its main objective is to find the local or global minima of a function based on its convexity. This determines in which direction the model should go to reduce the error.
There are three types of gradient descent:
- Mini-Batch Gradient Descent
- Stochastic Gradient Descent
- Batch Gradient Descent
11. Explain the different steps used in Gradient Descent Algorithm.
The five main steps that are used to initialize and use the gradient descent algorithm are as follows:
- Initialize biases and weights for the neural network.
- Pass the input data through the network i.e, the input layer.
- Compute the difference or the error between the expected and the predicted values.
- Adjust the values i.e, weight updation in neurons to minimize the loss function.
- We repeat the same steps i.e, multiple iterations to determine the best weights for efficient working.
12. Explain the term “Data Normalization”.
Data normalization is an essential preprocessing step that rescales the initial values to a specific range. It ensures better convergence during backpropagation.
In general, data normalization boils down each of the data points to subtracting the mean and dividing by its standard deviation. This technique improves the performance and stability of neural networks since we normalized the inputs in every layer.
13. What is the difference between Forward propagation and Backward Propagation in Neural Networks?
- Forward propagation: The input is fed into the network. In each layer, there is a specific activation function and between layers, there are weights that represent the connection strength of the neurons. The input runs through the individual layers of the network, which ultimately generates an output.
- Backward propagation: an error function measures how accurate the output of the network is. To improve the output, you need to optimize the weights. The backpropagation algorithm determines how to adjust the individual weights. You adjust the weights during the gradient descent method.
14. Explain the different types of Gradient Descent in detail.
- Stochastic Gradient Descent: In Stochastic gradient descent, a batch size of 1 is used. As a result, we get n batches. Therefore, the weights of the neural networks are updated after each training sample.
- Mini-batch Gradient Descent: In Mini-batch Gradient Descent, the batch size must be between 1 and the size of the training dataset. As a result, we get k batches. Therefore, the weights of the neural networks are updated after each mini-batch iteration.
- Batch Gradient Descent: In Batch Gradient Descent, the batch size is equal to the size of the training dataset. Therefore, the weights of the neural network are updated after each epoch.
15. What do you mean by Boltzmann Machine?
One of the most basic Deep Learning models is a Boltzmann Machine, which resembles a simplified version of the Multi-Layer Perceptron.
This model features a visible input layer and a hidden layer, creating a two-layer neural network that makes stochastic decisions about whether to activate a neuron.
In the Boltzmann Machine, nodes connect across the layers, but no two nodes within the same layer connect.
16. How does the learning rate affect the training of the Neural Network?
While selecting the learning rate to train the neural network, we have to choose the value very carefully due to the following reasons:
If the learning rate is set too low, training of the model will continue very slowly as we are making very small changes to the weights since our step size that is governed by the equation of gradient descent is small. It will take many iterations before reaching the point of minimum loss.
If the learning rate is set too high, this causes undesirable divergent behavior to the loss function due to large changes in weights due to a larger value of step size. It may fail to converge (the model can give a good output) or even diverge (data is too chaotic for the network to train).
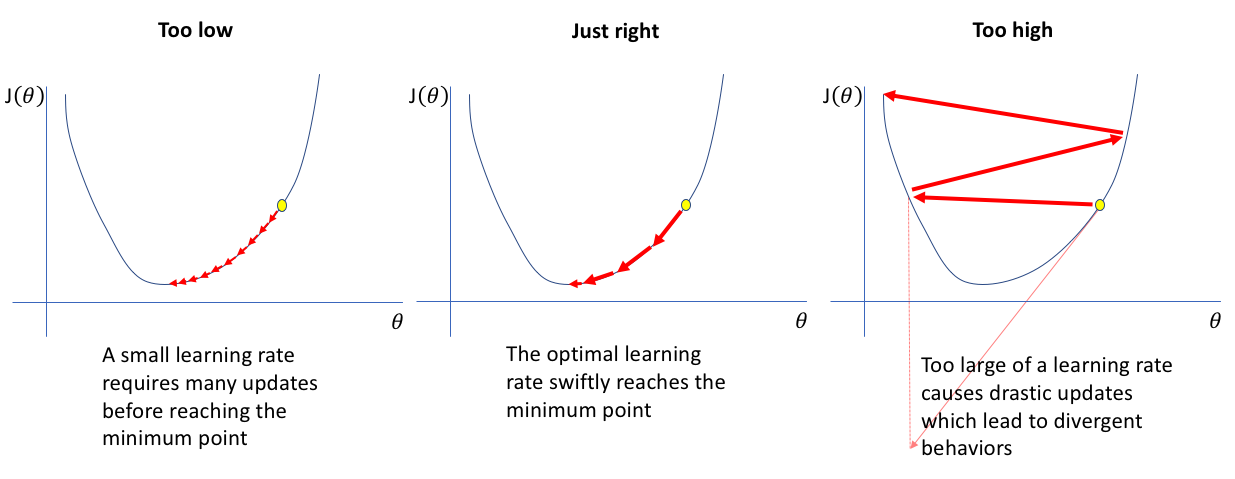
Image Source: Google Images
17. What do you mean by Hyperparameters?
Once you format the data correctly, you typically work with hyperparameters in neural networks. A hyperparameter is a type of parameter whose values you fix before the learning process begins.
It decides how a neural network is trained and also the structure of the network which includes:
- The number of hidden units
- The learning rate
- The number of epochs, etc.
18. Why is ReLU the most commonly used Activation Function?
ReLU (Rectified Linear Unit) is the most commonly used activation function in neural networks for the following reasons:
- No vanishing gradient: The derivative of the RELU activation function is either 0 or 1, so it could be not in the range of [0,1]. As a result, the product of several derivatives would also be either 0 or 1, because of this property, the vanishing gradient problem doesn’t occur during backpropagation.
- Faster training: Networks with RELU tend to show better convergence performance. Therefore, we have a much lower run time.
- Sparsity: For all negative inputs, a RELU generates an output of 0. This means that fewer neurons of the network are firing. So we have sparse and efficient activations in the neural network.
19. Explain the vanishing and exploding gradient problems.
These are the major problems in training deep neural networks.
While Backpropagation, in a network of n hidden layers, n derivatives will be multiplied together. If the derivatives are large e.g, If use ReLU like activation function then the value of the gradient will increase exponentially as we propagate down the model until they eventually explode, and this is what we call the problem of Exploding 3. gradient.
On the contrary, if the derivatives are small e.g, If use a Sigmoid activation function then the gradient will decrease exponentially as we propagate through the model until it eventually vanishes, and this is the Vanishing gradient problem.
20. What do you mean by Optimizers?
Optimizers are algorithms or methods that adjust the parameters of the neural network, such as weights, biases, and learning rate, to minimize the loss function. These algorithms solve optimization problems by minimizing the function.
The most common used optimizers in deep learning are as follows:
- Gradient Descent
- Stochastic Gradient Descent (SGD)
- Mini Batch Stochastic Gradient Descent (MB-SGD)
- SGD with momentum
- Nesterov Accelerated Gradient (NAG)
- Adaptive Gradient (AdaGrad)
- AdaDelta
- RMSprop
- Adam
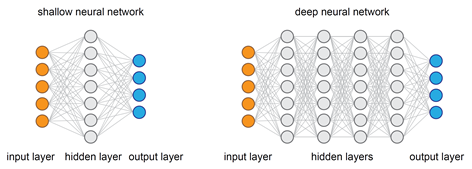
21. Why are Deep Neural Networks preferred over Shallow Neural Networks?
Neural networks contain hidden layers apart from input and output layers. There is only a single hidden layer between the input and output layers for shallow neural networks whereas, for Deep neural networks, there are multiple layers used.
To approximate any function, both shallow and deep networks are good enough and capable but when a shallow neural network fits into any function, it requires a lot of parameters to learn. On the contrary, deep networks can fit functions even better with a limited number of parameters since they contain several hidden layers.
So, for the same level of accuracy, deeper networks can be much more powerful and efficient in terms of both computation and the number of parameters to learn.
One other important thing about deeper networks is that they can create deep representations and at every layer, the network learns a new, more abstract representation of the input.
Therefore, in modern days deep neural networks have become preferable owing to their ability to work on any kind of data modeling.
22. Overfitting is one of the most common problems every Machine Learning practitioner faces. Explain some methods to avoid overfitting in Neural Networks.
Dropout: It is a regularization technique that prevents the neural network from overfitting. It randomly drops neurons from the neural network during training which is equivalent to training different neural networks. The different networks will overfit differently, so the net effect of the dropout regularization technique will be to reduce overfitting so that our model will be good for predictive analysis.

Early stopping: This regularization technique updates the model to make it better fit the training data with each iteration. After a certain number of iterations, new iterations improve the model. After that point, however, the model begins to overfit the training data. Early stopping refers to stopping the training process before that point.

23. What is the difference between Epoch, Batch, and Iteration in Neural Networks?
Epoch, iteration, and batch are different types that are used for processing the datasets and algorithms for gradient descent. All these three methods, i.e., epoch, iteration, and batch size are basically ways of working on the gradient descent depending on the size of the data set.
- Epoch: It represents one iteration over the entire training dataset (everything put into the training model).
- Batch: This refers to when we are not able to pass the entire dataset into the neural network at once due to the problem of high computations, so we divide the dataset into several batches.
- Iteration: Let’s have 10,000 images as our training dataset and we choose a batch size of 200. then an epoch should run (10000/200) iterations i.e, 50 iterations.
24. Suppose we have a perceptron having weights corresponding to the three inputs have the following values:
w1 = 2 ; w2 = −4; and w3 = 1
and the activation of the unit is given by the step-function:
φ(v) = 1 if v≥0 otherwise 0
Calculate the output value y of the given perceptron for each of the following input patterns:
| Pattern | P1 | P2 | P3 | P4 |
| X1 | 1 | 0 | 1 | 1 |
| X2 | 0 | 1 | 0 | 1 |
| X3 | 0 | 1 | 1 | 1 |
Solution:
To calculate the output value y for each of the given patterns we have to follow below two steps:
a) Calculate the weighted sum: v = Σi (wi xi)= w1 ·x1 +w2 ·x2 +w3 ·x3
b) Apply the activation function to v.
The calculations for each input pattern are:
P1 : v = 2·1−4·0+1·0=2, (2>0), y=φ(2)=1
P2 : v = 2·0−4·1+1·1=−3, (−3<0), y=φ(−3)=0
P3 : v = 2·1−4·0+1·1=3, (3>0), y=φ(3)=1
P4 : v = 2·1−4·1+1·1=−1, (−1<0), y=φ(−1)=0
25. Consider a feed-forward Neural Network having 2 inputs(label -1 and label -2 )with fully connected layers and we have 2 hidden layers:
Hidden layer-1: Nodes labeled as 3 and 4
Hidden layer-2: Nodes labeled as 5 and 6
A weight on the connection between nodes i and j is represented by wij, such as w24 is the weight on the connection between nodes 2 and 4. The following lists contain all the weights values used in the given network:
w13=−2, w35=1, w23 = 3, w45 = −1, w14 = 4, w36 = −1, w24=−1, w46=1
Each of the nodes 3, 4, 5, and 6 use the following activation function:
φ(v) = 1 if v≥0 otherwise 0
where v denotes the weighted sum of a node. Each of the input nodes (1 and 2) can only receive binary values (either 0 or 1). Calculate the output of the network (y5 and y6) for the input pattern given by (node-1 and node-2 as 0, 0 respectively).
Solution:
To find the output of the network it is necessary to calculate weighted sums of hidden nodes 3 and 4:
v3 =w13x1 +w23x2 , v4 =w14x1 +w24x2
Then find the outputs from hidden nodes using activation function φ:
y3 =φ(v3), y4 =φ(v4).
Use the outputs of the hidden nodes y3 and y4 as the input values to the output layer (nodes 5 and 6), and find weighted sums of output nodes 5 and 6:
v5 =w35y3 +w45y4 , v6 =w36y3 +w46y4 .
Finally, find the outputs from nodes 5 and 6 (also using φ):
y5 =φ(v5), y6 =φ(v6).
The output pattern will be (y5, y6).
Perform this calculation for the given input – Input pattern (0, 0)
v3 =−2·0+3·0=0, y3 =φ(0)=1
v4 =4·0−1·0=0, y4 =φ(0)=1
v5 =1·1−1·1=0, y5 =φ(0)=1
v6 =−1·1+1·1=0, y6 =φ(0)=1
Therefore, the output of the network for a given input pattern is (1, 1).
w1 = 2 ; w2 = −4; and w3 = 1
and the activation of the unit is given by the step-function:
φ(v) = 1 if v≥0 otherwise 0
Calculate the output value y of the given perceptron for each of the following input patterns:
| Pattern | P1 | P2 | P3 | P4 |
| X1 | 1 | 0 | 1 | 1 |
| X2 | 0 | 1 | 0 | 1 |
| X3 | 0 | 1 | 1 | 1 |
Solution:
To calculate the output value y for each of the given patterns we have to follow below two steps:
a) Calculate the weighted sum: v = Σi (wi xi)= w1 ·x1 +w2 ·x2 +w3 ·x3
b) Apply the activation function to v.
The calculations for each input pattern are:
P1 : v = 2·1−4·0+1·0=2, (2>0), y=φ(2)=1
P2 : v = 2·0−4·1+1·1=−3, (−3<0), y=φ(−3)=0
P3 : v = 2·1−4·0+1·1=3, (3>0), y=φ(3)=1
P4 : v = 2·1−4·1+1·1=−1, (−1<0), y=φ(−1)=0
Therefore, the output of the network for a given input pattern is (1, 1).
Thanks for reading!
Author – Chirag Goyal
Currently, I am pursuing my Bachelor of Technology (B.Tech) in Computer Science and Engineering from the Indian Institute of Technology Jodhpur(IITJ). I am very enthusiastic about Machine learning, Deep Learning, and Artificial Intelligence. Please feel free to contact me on Linkedin, Email.
I hope you enjoyed the questions and were able to test your knowledge about Artificial Neural Networks.
The author uses the media shown in this article at their discretion, and Analytics Vidhya does not own it.








Thanks, you, and I admire you to have the courage the talk about this, This was a very meaningful post for me. Thank you. custom on-demand app development
Interisting good work