Interview Prep
Career
GenAI
Prompt Engg
ChatGPT
LLM
Langchain
RAG
AI Agents
Machine Learning
Deep Learning
GenAI Tools
LLMOps
Python
NLP
SQL
AIML Projects

Reading list

Machine Learning Basics for a Newbie
6 Steps of Machine learning Lifecycle Introduction to Predictive Modeling
Introduction to Exploratory Data Analysis & Data Insights Descriptive Statistics Inferential Statistics How to Understand Population Distributions?
Reading Data Files into Python Different Variable Datatypes
Probability for Data Science Basic Concepts of Probability Axioms of Probability Conditional Probability
Central Tendencies for Continuous Variables Spread of Data KDE plots for Continuous Variable Overview of Distribution for Continuous variables Normal Distribution Skewed Distribution Skeweness and Kurtosis Distribution for Continuous Variable
Central Tendencies for Categorical Variables Understanding Discrete Distributions Performing EDA on Categorical Variables
Dealing with Missing Values Understanding Outliers Identifying Outliers in Data Outlier Detection in Python Outliers Detection Using IQR, Z-score, LOF and DBSCAN
Sample and Population Central Limit Theorem Confidence Interval and Margin of Error
Bivariate Analysis Introduction
Covariance Pearson Correlation Spearman's Correlation & Kendall's Tau Correlation versus Causation Tabular and Graphical methods for Bivariate Analysis Performing Bivariate Analysis on Continuous-Continuous Variables
Tabular and Graphical methods for Continuous-Categorical Variables Introduction to Hypothesis Testing P-value Two sample Z-test T-test T-test vs Z-test Performing Bivariate Analysis on Continuous-Catagorical variables
Chi-Squares Test Bivariate Analysis on Categorical Categorical Variables
Multivariate Analysis A Comprehensive Guide to Data Exploration The Data Science behind IPL
Supervised Learning vs Unsupervised Learning Reinforcement Learning Generative and Descriminative Models Parametric and Non Parametric model
Machine Learning Pipeline Preparing Dataset Build a Benchmark Model: Regression Build a Benchmark Model: Classification
Evaluation Metrics for Machine Learning Everyone should know Confusion Matrix Accuracy Precision and Recall AUC-ROC Log Loss R2 and Adjusted R2
Dealing with Missing Values Replacing Missing Values Imputing Missing Values in Data Working with Categorical Variables Working with Outliers Preprocessing Data for Model Building
Understanding Cost Function Understanding Gradient Descent Math Behind Gradient Descent Assumptions of Linear Regression Implement Linear Regression from Scratch Train Linear Regression in Python Implementing Linear Regression in R Diagnosing Residual Plots in Linear Regression Models Generalized Linear Models Introduction to Logistic Regression Odds Ratio Implementing Logistic Regression from Scratch Introduction to Scikit-learn in Python Train Logistic Regression in python Multiclass using Logistic Regression How to use Multinomial and Ordinal Logistic Regression in R ? Challenges with Linear Regression Introduction to Regularisation Implementing Regularisation Ridge Regression Lasso Regression
Introduction to K Nearest Neighbours Determining the Right Value of K in KNN Implement KNN from Scratch Implement KNN in Python
Bias Variance Tradeoff Introduction to Overfitting and Underfitting Visualizing Overfitting and Underfitting Selecting the Right Model What is Validation? Hold-Out Validation Understanding K Fold Cross Validation
Introduction to Feature Selection Feature Selection Algorithms Missing Value Ratio Low Variance Filter High Correlation Filter Backward Feature Elimination Forward Feature Selection Implement Feature Selection in Python Implement Feature Selection in R
Introduction to Decision Tree Purity in Decision Tree Terminologies Related to Decision Tree How to Select Best Split Point in Decision Tree? Chi-Squares Information Gain Reduction in Variance Optimizing Performance of Decision Tree Train Decision Tree using Scikit Learn Pruning of Decision Trees
Introduction to Feature Engineering Feature Transformation Feature Scaling Feature Engineering Frequency Encoding Automated Feature Engineering: Feature Tools
Introduction to Naive Bayes Conditional Probability and Bayes Theorem Introduction to Bayesian Adjustment Rating: The Incredible Concept Behind Online Ratings! Working of Naive Bayes Math behind Naive Bayes Types of Naive Bayes Implementation of Naive Bayes
Understanding how to solve Multiclass and Multilabled Classification Problem Evaluation Metrics: Multi Class Classification
Introduction to Ensemble Techniques Basic Ensemble Techniques Implementing Basic Ensemble Techniques Finding Optimal Weights of Ensemble Learner using Neural Network Why Ensemble Models Work well?
Introduction to Stacking Implementing Stacking Variants of Stacking Implementing Variants of Stacking Introduction to Blending Bootstrap Sampling Introduction to Random Sampling Hyper-parameters of Random Forest Implementing Random Forest Out-of-Bag (OOB) Score in the Random Forest IPL Team Win Prediction Project Using Machine Learning Introduction to Boosting Gradient Boosting Algorithm Math behind GBM Implementing GBM in python Regularized Greedy Forests Extreme Gradient Boosting Implementing XGBM in python Tuning Hyperparameters of XGBoost in Python Implement XGBM in R/H2O Adaptive Boosting Implementing Adaptive Boosing LightGBM Implementing LightGBM in Python Catboost Implementing Catboost in Python
Different Hyperparameter Tuning methods Implementing Different Hyperparameter Tuning methods GridsearchCV RandomizedsearchCV Bayesian Optimization for Hyperparameter Tuning Hyperopt
Understanding SVM Algorithm SVM Kernels In-depth Intuition and Practical Implementation SVM Kernel Tricks Kernels and Hyperparameters in SVM Implementing SVM from Scratch in Python and R
Introduction to Principal Component Analysis Steps to Perform Principal Compound Analysis Computation of Covariance Matrix Finding Eigenvectors and Eigenvalues Implementing PCA in python Visualizing PCA A Brief Introduction to Linear Discriminant Analysis Introduction to Factor Analysis
Introduction to Clustering Applications of Clustering Evaluation Metrics for Clustering Understanding K-Means Implementation of K-Means in Python Implementation of K-Means in R Choosing Right Value for K Profiling Market Segments using K-Means Clustering Hierarchical Clustering Implementation of Hierarchial Clustering DBSCAN Defining Similarity between clusters Build Better and Accurate Clusters with Gaussian Mixture Models
Understand Basics of Recommendation Engine with Case Study
8 Ways to Improve Accuracy of Machine Learning Models
Introduction to Dask Working with CuML
Introduction to Machine Learning Interpretability Framework and Interpretable Models model Agnostic Methods for Interpretability Implementing Interpretable Model Understanding SHAP Out-of-Core ML Introduction to Interpretable Machine Learning Models Model Agnostic Methods for Interpretability Game Theory & Shapley Values
Introduction to Machine Learning Interpretability Framework and Interpretable Models model Agnostic Methods for Interpretability Implementing Interpretable Model Understanding SHAP Out-of-Core ML Introduction to Interpretable Machine Learning Models Model Agnostic Methods for Interpretability Game Theory & Shapley Values
Introduction to AutoML Implementation of MLBox Introduction to PyCaret TPOT Auto-Sklearn EvalML
Pickle and Joblib Introduction to Model Deployment
Deploying Machine Learning Model using Streamlit Deploying ML Models in Docker Deploy Using Streamlit Deploy on Heroku Deploy Using Netlify Introduction to Amazon Sagemaker Setting up Amazon SageMaker Using SageMaker Endpoint to Generate Inference Deploy on Microsoft Azure Cloud Introduction to Flask for Model Deploying ML model using Flask
Model Deployment in Android Model Deployment in Iphone

Understanding Multiclass Classification Using SVM

Chirag Goyal
Chirag Goyal Last Updated : 23 Feb, 2024
7 min read

Introduction

Handwritten digit classification is one of the multiclass classification problem statements. In this article, we’ll introduce the multiclass classification using Support Vector Machines (SVM). We’ll first see what exactly is meant by multiclass classification, and we’ll discuss how SVM is applied for the multiclass classification problem. Finally, we’ll look at Python code for multiclass classification using Sklearn SVM.

The particular question on which we will be focusing in this article is as follows:

“How can you extend a binary classifier to a multi-class classifier in case of SVM algorithm?”

Multiclass Classification: In this type of classification, the machine learning model should classify an instance as only one of three classes or more. For Example, Classifying a text as positive, negative, or neutral.

Learning Objectives

  • Understand the concept of multiclass classification and its significance in solving complex classification problems.
  • Explore the fundamentals of Support Vector Machines (SVM) and their role in multiclass classification tasks.
  • Identify and compare three popular approaches for multiclass classification using SVM: One vs One (OVO), One vs All (OVA), and Directed Acyclic Graph (DAG).
  • Gain insights into the working principles of each approach, including their advantages, challenges, and implementation strategies.
  • Recognize key aspects such as regularization, kernel functions, and optimization techniques, and their impact on multiclass SVM performance.

This article was published as a part of the Data Science Blogathon.

Table of contents

What are Support Vector Machines (SVM)?

SVM is a supervised machine learning algorithm that helps in both classification and regression problem statements. It tries to find an optimal boundary (known as hyperplane) between different classes. In simple words, SVM does complex data transformations depending on the selected kernel function, and based on those transformations, it aims to maximize the separation boundaries between your data points.

  • Working of SVM: In the simplest form where there is a linear separation, SVM tries to find a line that maximizes the separation between a two-class data set of 2-dimensional space points.
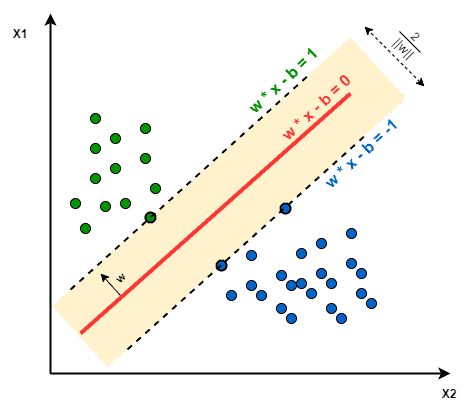
  • The objective of SVM: The objective of SVM is to find a hyperplane that maximizes the separation of the data points to their actual classes in an n-dimensional space. The data points which are at the minimum distance to the hyperplane i.e, closest points are called Support Vectors.

For example: In the given diagram, the support vectors consist of three points layered on the scattered lines, comprising 2 blue and 1 green support vectors, with the separation hyperplane represented by the solid red line.

Multiclass Classification Using SVM 1

Multiclass Classification Using SVM

In its most basic type, SVM doesn’t support multiclass classification. For multiclass classification, the same principle is utilized after breaking down the multi-classification problem into smaller subproblems, all of which are binary classification problems.

The popular methods that are used to perform multi-classification on the problem statements using SVM (multiclass support vector machines) are as follows:

  • One vs One (OVO) approach
  • Directed Acyclic Graph (DAG) approach
  • One vs All (OVA) approach

Now, let’s discuss each of these approaches one by one in a detailed manner:

One vs One (OVO)

This method decomposes our multiclass classification problem into binary subproblems. Consequently, we obtain binary classifiers for each pair of classes. To make final predictions, we employ majority voting along with the distance from the margin as a confidence criterion.

However, a significant drawback of this approach is the necessity to train numerous SVMs.

In the case of multi-class/multi-label problems with L categories, consider the (s, t)-th classifier:

  • Positive Samples: all points in class s ({ xi: s ∈ yi })
  • Negative samples: all points in class t ({ xi: t ∈ yi })
  • fs, t(x): decision value of this classifier (where a large value of fs, t(x) indicates a higher probability for label s over label t)
  • f t, s(x) = – f s, t(x)
  • Prediction: f(x) = argmax s ( Σ t fs, t(x) )

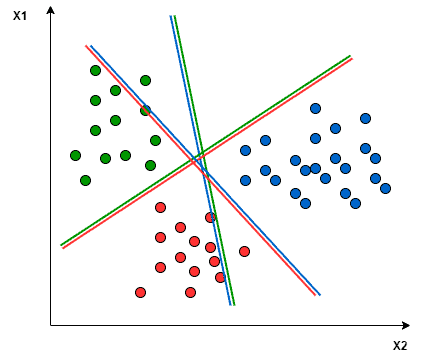
For instance, let’s consider a scenario with three class classification problems: Green, Red, and Blue.

Multiclass Classification Using SVM OVO

In the One-to-One approach, we aim to identify the hyperplane that separates every pair of classes, disregarding the points of the third class. For example, the Red-Blue line maximizes separation only between blue and red points, without considering the green points.

Multiclass Classification Using SVM 3

Also Read: Top 10 Machine Learning Algorithms to Use in 2024

One vs All (OVA)

In this technique, for an N class problem, we train N SVMs:

SVM number -1 learns “class_output = 1” vs “class_output ≠ 1”

SVM number -2 learns “class_output = 2” vs “class_output ≠ 2”

.
.
.
.

SVM number -N learns “class_output = N” vs “class_output ≠ N”

To predict the output for new input data, we predict with each of the built SVMs and then determine which one yields the prediction farthest into the positive region, acting as a confidence criterion for a specific SVM.

Challenges in N SVMs

However, there are challenges in training these N SVMs:

  • High Computation: Implementing the One vs All (OVA) strategy requires more training points, leading to increased computation.
  • Imbalanced Problems: For instance, in an MNIST dataset with 10 classes (0 to 9) and 1000 points per class, one SVM may have 9000 points while another has only 1000, resulting in an unbalanced problem.

To address this issue:

  • Utilize the 3-sigma rule of the normal distribution to fit data and subsample accordingly, maintaining class distribution.
  • Randomly select data points from the majority class.
  • Employ popular subsampling techniques like SMOTE.

For multi-class/multi-label problems with L categories:

For the t-th classifier:

  • Positive Samples: all points in class t ({ xi: t ∈ yi })
  • Negative samples: all points not in class t ({ xi: t ∉ yi })
  • ft(x): the decision value for the t-th classifier (where a large value of ft indicates a higher probability that x is in class t)
  • Prediction: f(x) = argmax t ft(x)

In the One vs All approach, a hyperplane is sought to separate the classes, considering all points and dividing them into two groups: one for the points of the class being analyzed and another for all other points.

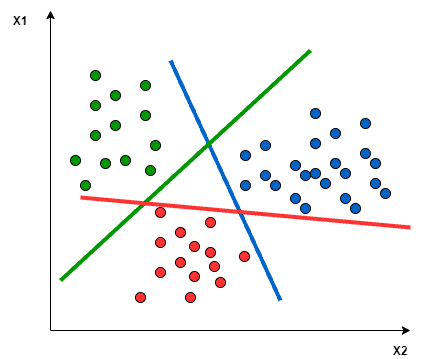
Multiclass Classification Using SVM OVA

A single SVM conducts binary classification and can differentiate between two classes. Accordingly:

  • In the One vs All approach, the classifier employs L SVMs.
  • In the One vs One approach, the classifier uses L(L-1)/2 SVMs.

Directed Acyclic Graph (DAG)

This approach is more hierarchical and aims to address the shortcomings of the One vs One and One vs All approach.

It adopts a graphical approach wherein classes are grouped based on logical categorization.

Benefits: This method offers advantages such as fewer SVM trains compared to the OVA approach, and it mitigates diversity issues from the majority class, which is a concern in the OVA approach.

Challenge: When the dataset doesn’t naturally come in distinct groups (e.g., CIFAR 10 image classification dataset), applying this approach directly becomes problematic. In such cases, identifying the logical grouping within the dataset becomes a manual task.

Conclusion

In conclusion, multiclass classification using Support Vector Machines (SVM) is a powerful approach for solving complex classification problems like handwritten digit recognition. SVMs extend binary classifiers to handle multiple class labels, enabling accurate classification into predefined categories.

We explored fundamental SVM concepts, including the objective of finding an optimal decision boundary and identifying support vectors. Three popular approaches for multiclass classification with SVMs were discussed: One vs One (OVO), One vs All (OVA), and Directed Acyclic Graph (DAG), each with unique advantages and challenges.

Key aspects such as regularization, kernel functions (linear, polynomial, radial basis function), and optimization techniques were highlighted, emphasizing the role of scikit-learn for implementation.

While this article covered essential concepts, advanced topics like cross-validation, decision boundaries, and model evaluation metrics remain unexplored. Additionally, topics like neural networks and non-linear SVMs offer alternative approaches to classification.

In summary, multiclass SVMs offer a robust framework for classifying data into multiple categories, making them valuable in data science and AI. By mastering these concepts, practitioners can build accurate models for various applications.

Key Takeaways

  • Multiclass classification using SVM extends binary classifiers to handle multiple class labels, enabling accurate classification into predefined categories like handwritten digit recognition.
  • Three main approaches for multiclass classification with SVM are One vs One (OVO), One vs All (OVA), and Directed Acyclic Graph (DAG), each with unique advantages and challenges.
  • The OVO approach breaks down the multiclass problem into binary subproblems, while OVA trains separate SVM classifiers for each class. DAG offers a hierarchical grouping approach, reducing diversity from the majority class.
  • Challenges in training multiple SVM classifiers include increased computation and unbalanced class distributions, which can be addressed through subsampling and techniques like SMOTE.
  • While this article covers essential concepts, advanced topics like cross-validation and model evaluation metrics remain unexplored, indicating further avenues for exploration in multiclass SVM classification.

Frequently Asked Questions

Q1. What is multiclass classification and its relation to Support Vector Machines (SVM)?

A. Multiclass classification involves categorizing instances into multiple classes, such as positive, negative, or neutral sentiments in text data. SVM tackles multiclass classification by breaking it into smaller binary classification subproblems, employing techniques like one-vs-rest or one-vs-one.

Q2. What are the common methods for multiclass classification using SVM?

A. Popular methods include one-vs-one (OVO), one-vs-all (OVA), and Directed Acyclic Graph (DAG) approaches. These methods divide the multiclass problem into binary subproblems, leveraging multiple SVM classifiers’ decision functions.

Q3. How does the one-vs-all (OVA) approach function in multiclass SVM classification?

A. In the OVA approach, each class has its SVM classifier, treating samples from that class as positive examples and others as negatives. The final prediction selects the class with the highest confidence score among all SVM classifiers.

Q4. What challenges come with training multiple SVM classifiers in the one-vs-all approach?

A. Training numerous SVM classifiers can pose issues like increased computation and unbalanced class distributions. Techniques like subsampling from the majority class or using SMOTE algorithms help mitigate these challenges and enhance classifier performance.

Q5. How does the Directed Acyclic Graph (DAG) approach differ from one-vs-all and one-vs-one methods in multiclass SVM classification?

A. The DAG approach is more hierarchical and aims to overcome limitations of OVA and OVO methods. It groups classes based on logical grouping, reducing diversity in the majority class. However, it may require manual class grouping unlike other approaches.

The media shown in this article are not owned by Analytics Vidhya and is used at the Author’s discretion. 

blogathonMulticlass ClassificationMulticlass Classification Using SVMSVM
Chirag Goyal
Chirag Goyal

I am a B.Tech. student (Computer Science major) currently in the pre-final year of my undergrad. My interest lies in the field of Data Science and Machine Learning. I have been pursuing this interest and am eager to work more in these directions. I feel proud to share that I am one of the best students in my class who has a desire to learn many new things in my field.

Free Courses

Generative AI 4.7

Generative AI - A Way of Life

Explore Generative AI for beginners: create text and images, use top AI tools, learn practical skills, and ethics.
Large Language Models 4.5

Getting Started with Large Language Models

Master Large Language Models (LLMs) with this course, offering clear guidance in NLP and model training made simple.
Prompt Engineering 4.6

Building LLM Applications using Prompt Engineering

This free course guides you on building LLM apps, mastering prompt engineering, and developing chatbots with enterprise data.
LlamaIndex 4.8

Improving Real World RAG Systems: Key Challenges & Practical Solutions

Explore practical solutions, advanced retrieval strategies, and agentic RAG systems to improve context, relevance, and accuracy in AI-driven applications.
RAG systems using LlamaIndex 4.7

Microsoft Excel: Formulas & Functions

Master MS Excel for data analysis with key formulas, functions, and LookUp tools in this comprehensive course.

Recommended Articles

Responses From Readers

Clear

Raymundo Addun
Raymundo Addun

I just admire your intelligence!!!

123

Write for us

Write, captivate, and earn accolades and rewards for your work
  • Reach a Global Audience
  • Get Expert Feedback
  • Build Your Brand & Audience
  • Cash In on Your Knowledge
  • Join a Thriving Community
  • Level Up Your Data Science Game
imag

We use cookies essential for this site to function well. Please click to help us improve its usefulness with additional cookies. Learn about our use of cookies in our Privacy Policy & Cookies Policy.

Show details