When the Measurement’s Accuracy Misleads you!

Introduction on Measurements Accuracy

You’ve undoubtedly heard about gold diggers as well. In the majority of these cases, individuals discover enormous wealth with the aid of gold diggers and become overnight millionaires.

Your friend has a gold detector. You, too, have chosen to join the group of Gold Seekers in order to help your buddy. So you and a friend go to a mine with around 1000 stones in it, and you guess that 1% of these stones are gold.

When gold is identified, your friend’s gold detector will beep, and the method is as follows:

• This device detects gold and constantly beeps when it comes into contact with gold.
• This device is 90% accurate in identifying gold from stones

As you and your fellow explore the mine, the machine beeps in front of one of the rocks. If this stone is gold, its market value is about $1,000. Your buddy recommends that you pay him $ 250 and pick up the stone. The deal seems appealing because you earn three times as much money if it’s gold. On the other hand, the gold detector’s accuracy is great, as is the likelihood of gold being gold. These are the thoughts that will finally encourage you to pay $ 250 to your buddy and pick up the stone for yourself.

It is not a bad idea to take a step back from the world of gold seekers and return to the beautiful world of mathematics to examine the problem more closely:

• Given that there are approximately 1000 stones in this mine and that 1% of them are gold, this means that there are about 10 gold stones in this mine.
• As a result, approximately 990 stones in this mine have no unique material value.
• The device’s accuracy in distinguishing gold from stones is 90%, which means that if we put 990 stones (which we are certain are not gold) in front of it, it will mistakenly sound for about 99 stones.

Given the foregoing, it is likely that if we turn this device in the mine, it will sound 109 times, even though only 10 beeps are truly gold. This means that there is only a 9% chance that the stone we paid $250 for is gold. That means we didn’t do a good deal and probably wasted $250 on a piece of worthless stone. If we want to mathematically summarize all of these conversations, we will have:

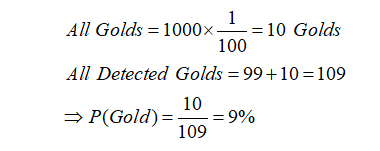
After investigating this issue mathematically, we discovered that the “measurement accuracy” parameter alone is insufficient to achieve a reliable result and that other factors must be considered. The “false positive paradox” is a concept used in statistics and data science to describe this argument.

This paradox typically occurs when the probability of an event occurring is less than the error accuracy of the instrument used to measure the event. For example, in the case of “gold diggers,” we used a device with 90% accuracy (10% error) to investigate an event with a 1% probability, so the results were not very reliable.

Familiarity with Terminology

Before delving into the concerns surrounding the “false positive paradox,” it’s a good idea to brush up on a few statistical cases. Assume that a corona test has been performed to help you understand the notion. This test yielded four modes:

• True Positive: You are infected with the Coronavirus and the test is positive.
• False Positive: You have not been infected with the Coronavirus, yet the test is positive.
• True Negative: You have not been infected with the Coronavirus, and the test result is negative.
• False Negative: You have been infected with the Coronavirus, but the test results are negative.

It should be mentioned that the corona test and medical tests, in general, are used as examples here, and these four requirements may be applied to any event in which there is a risk of inaccuracy.

In the instance of gold seekers, the percentage of false-positive error of the device, i.e. if the device is not gold but the device beeps, was 10%, and the percentage of false-negative error of the device, i.e. if the device is gold but the device does not beep, was 0%. In the next sections, we will look at some different aspects of the “false positive paradox” debate.

Measurements Accuracy: Unknown Virus

A mysterious virus has infected a city of 10,000 people, impacting roughly 40% of the population. As a product manager, you focus on creating the viral detection kit as quickly as feasible in order to distinguish infected persons from healthy people.

Your ID kit has a 5% false-positive error rate and a 0% false-negative error rate. This kit is currently being utilized to detect sick persons in the city, and your predicted outcomes are as follows:

• Estimated number of people with the disease:

• Number of false positive test results:
  

  

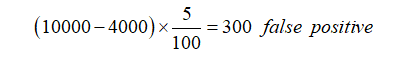
As previously stated, the false-negative percentage of this kit is 0%, implying that if someone has a condition, it must be recognized. It has recently been found that around 300 people’s test results were deemed incorrect. Finally, it is possible to state that the test result was positive for 4300 persons, with 4000 of them really having the condition. As a result, the measurement accuracy of this kit is around 93 percent, which is a respectable figure that can be relied on.

However, this is not the end of the story! As your company’s detection kit has been effective, it is now being used to identify infections in other cities. One of these cities has a population of approximately 1,000 people, and about 2% of the residents in this little hamlet are afflicted with the virus.The affected persons were identified using an identifying kit; however, the findings were disappointing. The vast majority of those who tested positive showed no signs of illness, calling into doubt the legitimacy and quality of your company’s kit. We can reach the following results with a little computation:

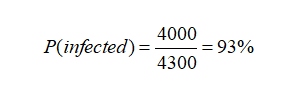
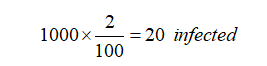
• Estimated number of people with the disease:

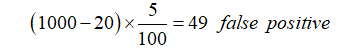
• The number of false-positive test results:

It is obvious that the test findings are invalid. While just 20 persons were infected with the virus, the identification kit tested positive for 69 people, or roughly 29 per cent, an extremely low figure for a medical test:

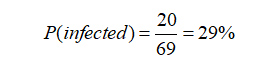
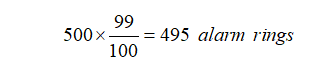 In other words, if an individual test results in a positive result in this test, it is more than 70% likely that he is not sick! We are also confronted with a “false positive contradiction” here. As previously stated, the findings are invalid if the likelihood of an event occurring is smaller than the error rate of the instrument used to measure that event. In this case, the detection kit’s false positive error rate is around 5%, whereas the chance of illness incidence in a small town is at 2%. As a result, the acquired findings are not exceptionally reliable. As a product manager, you must now create a protocol and a safety margin for the identification kit in order to assess how trustworthy the kit’s results are.

Measurements Accuracy: Alarm Warning

In one of the most significant metropolitan retail complexes with a population of one million people, an anti-terrorist camera and siren have been placed. This siren has a 1% chance of being false positive and a 1% chance of being false negative. To put it another way, we can say:

False Negative: If a CCTV camera identifies a terrorist, the alarm will go off 99 per cent of the time.

False Positive: When regular persons pass in front of the camera, the alarm is 99 per cent less likely to sound, but it is 1 per cent more likely to ring.

The concern now is, if the alarm goes off one day, what is the likelihood that there is a terrorist within the complex?

We estimate that there are 500 terrorists in a metropolis of 1 million people. This assumption is plausible and supported by demographic and statistical data. Now we return to the original question: what is the likelihood of a terrorist being within the complex if the alarm goes off? The following calculations are used to arrive at this percentage.

Given the reconnaissance camera’s 99 per cent accuracy, there are 500 terrorists in the city, and if they all pass in front of the camera, the siren will sound 495 times:

99,900 are regular folks (the entire population of the city minus the terrorists) If all of these persons pass in front of the camera, the alert rings 9995 times due to the recognition camera’s 1% error:

As a result, if the entire city passes in front of this camera, the siren will ring 10490 times. However, the siren only sounded properly in 495 of the cases. It is now possible to assess what proportion of terrorists would be present if a siren sound:

According to these estimates, if the alarm goes off, it is more than 95 per cent likely to be false, and there is no terrorist within the complex. The end outcome is considerably different from our original concept. Most people are astonished by this outstanding precision when they read about the camera’s 99 per cent accuracy and believe that the majority of the output of this gadget would be right, but we have once again demonstrated that measurement accuracy alone is insufficient.

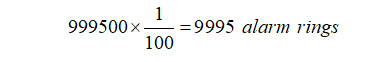
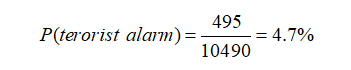
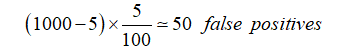
Test of Consciousness

An alert device has entrusted you with product management. Police will use the gadget to detect drivers who have drunk alcohol or used drugs. The following are the specs for the product produced by your team:

• This equipment has a zero per cent false-negative error rate, which indicates that it accurately screens all persons who have used alcohol or drugs.
• This gadget has a false positive error rate of roughly 5%, which means that in 95 per cent of situations, the test result for those who haven’t used drugs or alcohol is negative. Still, in 5% of cases, the test result is positive.

You spend some time thinking about product releases and ask the police to provide you with a study on the incidence of alcohol and drug use among drivers because you are adept in data science and have been a data scientist before taking on product management.

Following an examination of the data, you will discover that, on average, 5 out of every 1,000 drivers had ingested alcohol and drugs. This is a bit of a problem since if the police randomly test drivers with your existing product, it might lead to a disaster! We undertake the following computations to have a better understanding of this problem.

Five individuals out of every thousand have taken alcohol and drugs, and because the device’s false-negative error rate is zero per cent, the test of these five people will be positive.

As previously stated, the device’s false positive error rate is around 5%. This means that around 50 of the 995 drivers who have not drunk will test positive:

This indicates that just 5 persons have been confirmed right out of 55 positive tests published among 1000 people. This shows that the test’s accuracy is around 9%, and if someone tests positive, it is more than 90% probable that it was not ingested and is hence innocent!

 As a result, it is evident that using this gadget at random would be very error-prone and will badly harm your firm’s reputation and the police department. To fix this difficulty, the circle of persons must be somewhat restricted. In other words, you should devise a way in which the likelihood of a person taking alcohol or drugs was more significant than the device’s inaccuracy. So you create a code of conduct in which you specify behaviours that, if a driver does any of them, they have a 60% likelihood of ingesting alcohol or drugs. This will provide credence to the device’s output. To be sure, imagine cops halted a group of 100 drivers who were sceptical of the method.

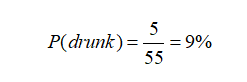
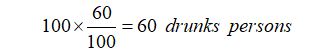
Given that the chance of consumption among these people is 60%, in a group of 100 people, approximately 60 people have consumed, hence the test of these 60 people will be positive:

Because the gadget has a 5% mistake rate, two of the remaining 40 persons are likely to test positive:

As a result, it was discovered that even a basic understanding of the sample space had a significant impact on the outcome. Of course, being aware of your sample space is a lengthy issue that we will return to in future posts.

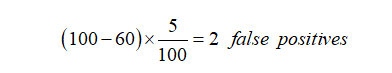
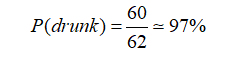
Conclusion

According to the findings, the measurement precision of a device alone cannot ensure the reliability of the output, and the sample space under consideration is maybe more essential than the instrument’s accuracy. To avoid the effect of a “false positive paradox,” conditions must be constructed in which the chance of occurrence exceeds the device’s inaccuracy. In the instance of the “awareness test,” this resulted in a significant boost in output accuracy.

Read more articles on our website. Here is the link.

Thanks for reading!

Follow me on Medium, LinkedIn and Twitter.

 

The media shown in this article is not owned by Analytics Vidhya and are used at the Author’s discretion. 

Jalil Alizadeh 07 Apr 2022