This article was published as a part of the Data Science Blogathon.

Introduction
In this article, we will learn how to make an object tracker using OpenCV in Python and using, and we will build an object tracker and make a counter system.
A tracker keeps track of moving objects in the frame; In OpenCV, we can build a tracker class using Euclidean distance tracking or centroid tracking.
Object tracking and the counter system are only used in video or camera feed. Our tracker will assign a specific id to the moving objects, which will not change throughout the feed.
Generally, there could be two types of object trackers based on their capabilities.
- Multiple Object Tracker
- Single Object Tracker
In this article, we will design a Multiple Object Tracker, and using that; we will make a Vehicle Counter System using Python.
Available Tracking Algorithms
There are various tracking algorithms available in the market. They have different working algorithms and complexity.
Some Popular tracking algorithms are given below-
- DEEP SORT: This is one of the most popular tracker algorithms which uses deep learning. This works combined with the YOLO object detector. In the backend, it uses various filters, including Kalman’s filter, for its tracking. Deep learning-based models often overperform the classical machine learning models.
- Centroid Tracker algorithm: Centroid tracker algorithms are all about tracking the coordinates by defining some threshold values to be called as same points. There is no machine learning stuff involved in it. This algorithm is a multiple-step process where we calculate the euclidean distance of centroids of all detected objects in subsequent frames. We will make a custom python class to implement Centroid tracking.
Centroid Tracker Algorithm Process
Step 1. In the first step, moving objects will be detected, and a bounding box for each and every moving object will be found. Using the bounding box coordinates, the centroid points will be calculated, which will be the point of diagonal intersection of the bounding box rectangle.
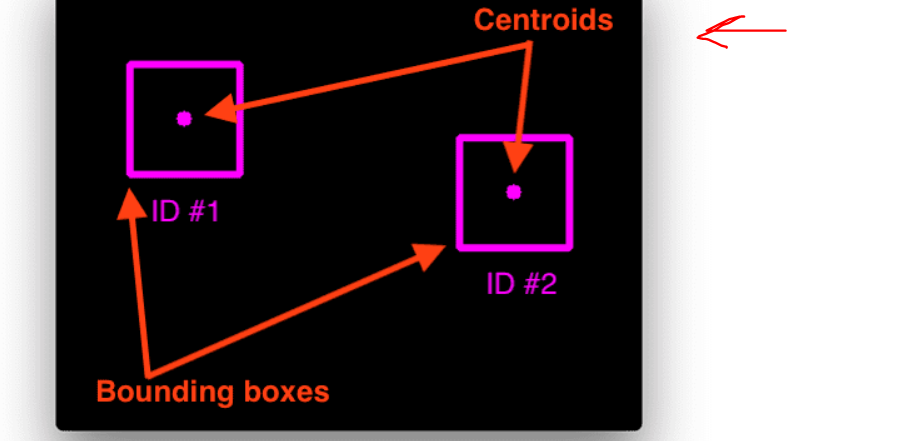
Centroids calculation
Step 2. After calculating the centroid points, assign them a specific unique id and then calculate the euclidean distance between every possible centroid in our frame.
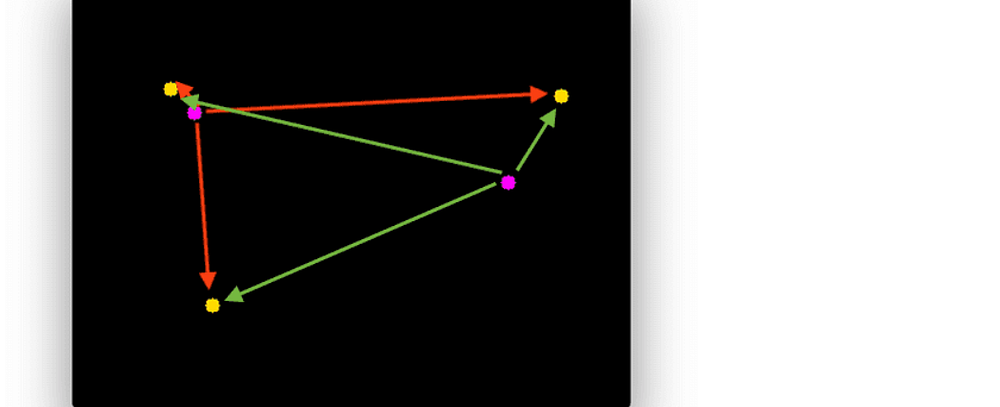
Euclidean Distance between centroids
Step 3. The main Idea of Centroid is that the same object will be moved a minimum distance compared to others points in the subsequent frames. Using this idea,, whichever centroid has the minimum distance pair will be assigned with the same id as the previous centroid with the least euclidean distance.
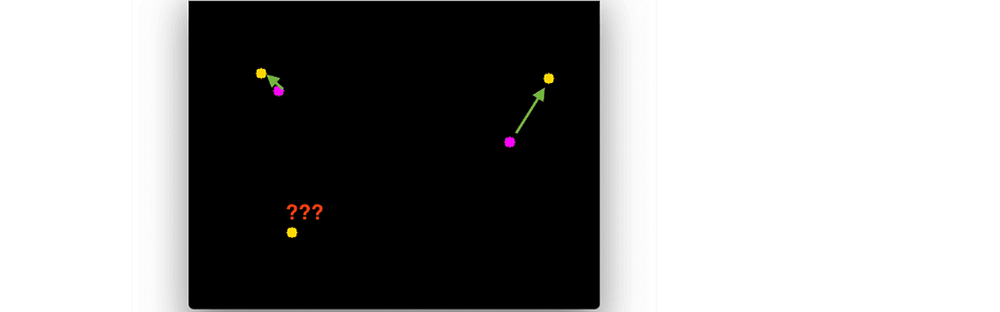
Centroid distance difference
Step 4. We can assign previous IDs to the object in the subsequent frame based on the euclidean distance difference.

Points being Tracked
We are using the subtraction technique on subsequent frames to capture the moving points ( F(t+1) -F(t)). However, we are free to use any object detector algorithms based on our objective.
Application of Object Tracking
The involvement of deep learning in Object tracking makes it more robust daily. Modern object trackers are far better than what we have seen previously. These Object Trackers are being deployed extensively.
- Tracking Unwanted Behaviours
- Crowd Detection
- Vehicle Tracking
- In the Aviation Industry
- Tracker in the Malls and Shopping Complexes
- Security Systems
Euclidean Distance Tracker in Python
By Combining all the Processes we discussed, we made a EuclideanDistTracker class In Python. This Tracker Object will return me the tracking Id and coordinates of the moving objects.
This Class Contains all the math involved in Object Tracking.
<?xml version="1.0"?>
<!-- Add more negative to training. -->
<opencv_storage>
<cars3 type_id="opencv-haar-classifier">
<size>
20 20</size>
<stages>
<_>
<!-- stage 0 -->
<trees>
<_>
<!-- tree 0 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
6 12 8 8 -1.</_>
<_>
6 16 8 4 2.</_></rects>
<tilted>0</tilted></feature>
<threshold>0.0452074706554413</threshold>
<left_val>-0.7191650867462158</left_val>
<right_val>0.7359663248062134</right_val></_></_>
<_>
<!-- tree 1 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
1 12 18 1 -1.</_>
<_>
7 12 6 1 3.</_></rects>
<tilted>0</tilted></feature>
<threshold>-0.0161712504923344</threshold>
<left_val>0.5866637229919434</left_val>
<right_val>-0.5909150242805481</right_val></_></_>
<_>
<!-- tree 2 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
7 18 5 2 -1.</_>
<_>
7 19 5 1 2.</_></rects>
<tilted>0</tilted></feature>
<threshold>0.0119725503027439</threshold>
<left_val>-0.3645753860473633</left_val>
<right_val>0.8175076246261597</right_val></_></_>
<_>
<!-- tree 3 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
5 12 11 4 -1.</_>
<_>
5 14 11 2 2.</_></rects>
<tilted>0</tilted></feature>
<threshold>0.0554178208112717</threshold>
<left_val>-0.5766019225120544</left_val>
<right_val>0.8059020042419434</right_val></_></_></trees>
<stage_threshold>-1.0691740512847900</stage_threshold>
<parent>-1</parent>
<next>-1</next></_>
<_>
<!-- stage 1 -->
<trees>
<_>
<!-- tree 0 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
1 12 18 2 -1.</_>
<_>
7 12 6 2 3.</_></rects>
<tilted>0</tilted></feature>
<threshold>-0.0243058893829584</threshold>
<left_val>0.5642552971839905</left_val>
<right_val>-0.7375097870826721</right_val></_></_>
<_>
<!-- tree 1 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
3 1 14 6 -1.</_>
<_>
3 3 14 2 3.</_></rects>
<tilted>0</tilted></feature>
<threshold>-0.0302439108490944</threshold>
<left_val>0.5537161827087402</left_val>
<right_val>-0.5089462995529175</right_val></_></_>
<_>
<!-- tree 2 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
4 8 12 9 -1.</_>
<_>
4 11 12 3 3.</_></rects>
<tilted>0</tilted></feature>
<threshold>-0.1937028020620346</threshold>
<left_val>0.7614368200302124</left_val>
<right_val>-0.3485977053642273</right_val></_></_>
<_>
<!-- tree 3 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
8 18 12 2 -1.</_>
<_>
14 18 6 1 2.</_>
<_>
8 19 6 1 2.</_></rects>
<tilted>0</tilted></feature>
<threshold>0.0120156398043036</threshold>
<left_val>-0.4035871028900146</left_val>
<right_val>0.6296288967132568</right_val></_></_>
<_>
<!-- tree 4 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
0 12 6 6 -1.</_>
<_>
2 12 2 6 3.</_></rects>
<tilted>0</tilted></feature>
<threshold>2.9895049519836903e-03</threshold>
<left_val>-0.4086846113204956</left_val>
<right_val>0.4285241067409515</right_val></_></_>
<_>
<!-- tree 5 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
6 11 9 8 -1.</_>
<_>
6 15 9 4 2.</_></rects>
<tilted>0</tilted></feature>
<threshold>0.1299877017736435</threshold>
<left_val>-0.2570166885852814</left_val>
<right_val>0.5929297208786011</right_val></_></_>
<_>
<!-- tree 6 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
1 6 10 2 -1.</_>
<_>
1 6 5 1 2.</_>
<_>
6 7 5 1 2.</_></rects>
<tilted>0</tilted></feature>
<threshold>-6.0164160095155239e-03</threshold>
<left_val>0.5601549744606018</left_val>
<right_val>-0.2849527895450592</right_val></_></_></trees>
<stage_threshold>-1.0788700580596924</stage_threshold>
<parent>0</parent>
<next>-1</next></_>
<_>
<!-- stage 2 -->
<trees>
<_>
<!-- tree 0 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
3 2 14 12 -1.</_>
<_>
3 6 14 4 3.</_></rects>
<tilted>0</tilted></feature>
<threshold>0.0943963602185249</threshold>
<left_val>-0.5406976938247681</left_val>
<right_val>0.5407304763793945</right_val></_></_>
<_>
<!-- tree 1 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
1 11 18 9 -1.</_>
<_>
7 11 6 9 3.</_></rects>
<tilted>0</tilted></feature>
<threshold>-0.0279577299952507</threshold>
<left_val>0.3281945884227753</left_val>
<right_val>-0.7144141197204590</right_val></_></_>
<_>
<!-- tree 2 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
5 12 10 4 -1.</_>
<_>
5 14 10 2 2.</_></rects>
<tilted>0</tilted></feature>
<threshold>0.0635356530547142</threshold>
<left_val>-0.3744345009326935</left_val>
<right_val>0.5956786870956421</right_val></_></_>
<_>
<!-- tree 3 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
6 18 9 2 -1.</_>
<_>
6 19 9 1 2.</_></rects>
<tilted>0</tilted></feature>
<threshold>0.0211040005087852</threshold>
<left_val>-0.4845815896987915</left_val>
<right_val>0.7378302812576294</right_val></_></_>
<_>
<!-- tree 4 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
9 12 2 8 -1.</_>
<_>
9 16 2 4 2.</_></rects>
<tilted>0</tilted></feature>
<threshold>2.6957250665873289e-03</threshold>
<left_val>-0.8702409863471985</left_val>
<right_val>0.2475769072771072</right_val></_></_>
<_>
<!-- tree 5 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
15 3 3 16 -1.</_>
<_>
15 11 3 8 2.</_></rects>
<tilted>0</tilted></feature>
<threshold>0.0110464803874493</threshold>
<left_val>-0.5981134176254272</left_val>
<right_val>0.1849218010902405</right_val></_></_>
<_>
<!-- tree 6 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
7 9 1 6 -1.</_>
<_>
7 11 1 2 3.</_></rects>
<tilted>0</tilted></feature>
<threshold>-1.3549139839597046e-04</threshold>
<left_val>0.3266639113426208</left_val>
<right_val>-0.8332661986351013</right_val></_></_>
<_>
<!-- tree 7 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
6 0 8 6 -1.</_>
<_>
6 3 8 3 2.</_></rects>
<tilted>0</tilted></feature>
<threshold>-0.0495516993105412</threshold>
<left_val>0.7439032196998596</left_val>
<right_val>-0.4024896025657654</right_val></_></_>
<_>
<!-- tree 8 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
1 13 6 1 -1.</_>
<_>
4 13 3 1 2.</_></rects>
<tilted>0</tilted></feature>
<threshold>-1.9892829004675150e-03</threshold>
<left_val>0.5047793984413147</left_val>
<right_val>-0.5123764276504517</right_val></_></_>
<_>
<!-- tree 9 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
10 10 6 1 -1.</_>
<_>
12 10 2 1 3.</_></rects>
<tilted>0</tilted></feature>
<threshold>-5.7016697246581316e-04</threshold>
<left_val>0.2391823977231979</left_val>
<right_val>-0.2104973942041397</right_val></_></_>
<_>
<!-- tree 10 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
4 10 6 1 -1.</_>
<_>
6 10 2 1 3.</_></rects>
<tilted>0</tilted></feature>
<threshold>5.4985969327390194e-03</threshold>
<left_val>-0.3141318857669830</left_val>
<right_val>0.7439212799072266</right_val></_></_>
<_>
<!-- tree 11 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
6 6 8 3 -1.</_>
<_>
6 7 8 1 3.</_></rects>
<tilted>0</tilted></feature>
<threshold>-7.7209789305925369e-03</threshold>
<left_val>0.6021335721015930</left_val>
<right_val>-0.3841854035854340</right_val></_></_></trees>
<stage_threshold>-1.5200910568237305</stage_threshold>
<parent>1</parent>
<next>-1</next></_>
<_>
<!-- stage 3 -->
<trees>
<_>
<!-- tree 0 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
1 12 14 1 -1.</_>
<_>
8 12 7 1 2.</_></rects>
<tilted>0</tilted></feature>
<threshold>-1.1992900399491191e-03</threshold>
<left_val>0.2906270921230316</left_val>
<right_val>-0.7548354268074036</right_val></_></_>
<_>
<!-- tree 1 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
5 2 15 12 -1.</_>
<_>
5 6 15 4 3.</_></rects>
<tilted>0</tilted></feature>
<threshold>0.0943495184183121</threshold>
<left_val>-0.4595882892608643</left_val>
<right_val>0.3241611123085022</right_val></_></_>
<_>
<!-- tree 2 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
7 18 6 2 -1.</_>
<_>
7 19 6 1 2.</_></rects>
<tilted>0</tilted></feature>
<threshold>0.0227251593023539</threshold>
<left_val>-0.2826507091522217</left_val>
<right_val>0.7242512702941895</right_val></_></_>
<_>
<!-- tree 3 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
5 12 10 4 -1.</_>
<_>
5 14 10 2 2.</_></rects>
<tilted>0</tilted></feature>
<threshold>0.0585403405129910</threshold>
<left_val>-0.5193219780921936</left_val>
<right_val>0.6013407111167908</right_val></_></_>
<_>
<!-- tree 4 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
2 19 4 1 -1.</_>
<_>
4 19 2 1 2.</_></rects>
<tilted>0</tilted></feature>
<threshold>2.8358890631352551e-05</threshold>
<left_val>-0.6561384201049805</left_val>
<right_val>0.3897354006767273</right_val></_></_>
<_>
<!-- tree 5 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
10 12 10 8 -1.</_>
<_>
10 16 10 4 2.</_></rects>
<tilted>0</tilted></feature>
<threshold>3.9341559750027955e-04</threshold>
<left_val>-0.8008638024330139</left_val>
<right_val>0.2018187046051025</right_val></_></_>
<_>
<!-- tree 6 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
1 13 6 6 -1.</_>
<_>
4 13 3 6 2.</_></rects>
<tilted>0</tilted></feature>
<threshold>-5.8259762590751052e-04</threshold>
<left_val>0.2970958054065704</left_val>
<right_val>-0.8628513216972351</right_val></_></_>
<_>
<!-- tree 7 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
9 18 6 2 -1.</_>
<_>
12 18 3 1 2.</_>
<_>
9 19 3 1 2.</_></rects>
<tilted>0</tilted></feature>
<threshold>2.7955149562330917e-05</threshold>
<left_val>-0.4508801102638245</left_val>
<right_val>0.1758446991443634</right_val></_></_>
<_>
<!-- tree 8 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
1 10 9 10 -1.</_>
<_>
1 15 9 5 2.</_></rects>
<tilted>0</tilted></feature>
<threshold>1.2162160128355026e-03</threshold>
<left_val>-0.8695623278617859</left_val>
<right_val>0.2619656026363373</right_val></_></_>
<_>
<!-- tree 9 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
1 2 18 5 -1.</_>
<_>
7 2 6 5 3.</_></rects>
<tilted>0</tilted></feature>
<threshold>0.0133769698441029</threshold>
<left_val>-0.6464508175849915</left_val>
<right_val>0.3887208998203278</right_val></_></_>
<_>
<!-- tree 10 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
1 12 18 4 -1.</_>
<_>
7 12 6 4 3.</_></rects>
<tilted>0</tilted></feature>
<threshold>-0.0113867800682783</threshold>
<left_val>0.2826564013957977</left_val>
<right_val>-0.8351002931594849</right_val></_></_>
<_>
<!-- tree 11 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
9 11 6 3 -1.</_>
<_>
9 11 3 3 2.</_></rects>
<tilted>0</tilted></feature>
<threshold>2.6949660386890173e-03</threshold>
<left_val>-0.5282859802246094</left_val>
<right_val>0.6657627820968628</right_val></_></_>
<_>
<!-- tree 12 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
5 10 3 2 -1.</_>
<_>
6 10 1 2 3.</_></rects>
<tilted>0</tilted></feature>
<threshold>2.8329479391686618e-05</threshold>
<left_val>-0.6864507794380188</left_val>
<right_val>0.5240061283111572</right_val></_></_>
<_>
<!-- tree 13 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
8 12 9 8 -1.</_>
<_>
8 16 9 4 2.</_></rects>
<tilted>0</tilted></feature>
<threshold>1.4069270109757781e-03</threshold>
<left_val>-0.8969905972480774</left_val>
<right_val>0.2389785945415497</right_val></_></_>
<_>
<!-- tree 14 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
6 1 3 2 -1.</_>
<_>
6 2 3 1 2.</_></rects>
<tilted>0</tilted></feature>
<threshold>-2.9115570214344189e-05</threshold>
<left_val>0.4608972072601318</left_val>
<right_val>-0.8574141860008240</right_val></_></_>
<_>
<!-- tree 15 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
2 12 18 6 -1.</_>
<_>
2 14 18 2 3.</_></rects>
<tilted>0</tilted></feature>
<threshold>4.5082978904247284e-03</threshold>
<left_val>-0.7511271238327026</left_val>
<right_val>0.4849173128604889</right_val></_></_>
<_>
<!-- tree 16 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
0 11 18 1 -1.</_>
<_>
6 11 6 1 3.</_></rects>
<tilted>0</tilted></feature>
<threshold>-0.0198406204581261</threshold>
<left_val>0.6246759295463562</left_val>
<right_val>-0.7629678845405579</right_val></_></_>
<_>
<!-- tree 17 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
9 5 6 3 -1.</_>
<_>
9 6 6 1 3.</_></rects>
<tilted>0</tilted></feature>
<threshold>3.8021910004317760e-03</threshold>
<left_val>-0.4809493124485016</left_val>
<right_val>0.6243296861648560</right_val></_></_>
<_>
<!-- tree 18 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
3 11 4 6 -1.</_>
<_>
3 14 4 3 2.</_></rects>
<tilted>0</tilted></feature>
<threshold>1.1158349661855027e-04</threshold>
<left_val>-0.8559886217117310</left_val>
<right_val>0.3861764967441559</right_val></_></_>
<_>
<!-- tree 19 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
12 18 2 2 -1.</_>
<_>
13 18 1 1 2.</_>
<_>
12 19 1 1 2.</_></rects>
<tilted>0</tilted></feature>
<threshold>2.7662550564855337e-05</threshold>
<left_val>-0.7629433274269104</left_val>
<right_val>0.3604950010776520</right_val></_></_>
<_>
<!-- tree 20 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
3 12 9 8 -1.</_>
<_>
3 16 9 4 2.</_></rects>
<tilted>0</tilted></feature>
<threshold>2.7047859039157629e-03</threshold>
<left_val>-0.9496951103210449</left_val>
<right_val>0.3921845853328705</right_val></_></_>
<_>
<!-- tree 21 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
6 12 9 2 -1.</_>
<_>
9 12 3 2 3.</_></rects>
<tilted>0</tilted></feature>
<threshold>5.1935878582298756e-04</threshold>
<left_val>-0.8682754039764404</left_val>
<right_val>0.4790566861629486</right_val></_></_>
<_>
<!-- tree 22 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
2 12 12 8 -1.</_>
<_>
2 12 6 4 2.</_>
<_>
8 16 6 4 2.</_></rects>
<tilted>0</tilted></feature>
<threshold>1.0928940173471346e-04</threshold>
<left_val>-0.9670708775520325</left_val>
<right_val>0.6848754286766052</right_val></_></_>
<_>
<!-- tree 23 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
1 6 19 3 -1.</_>
<_>
1 7 19 1 3.</_></rects>
<tilted>0</tilted></feature>
<threshold>5.7576759718358517e-03</threshold>
<left_val>-0.9778658747673035</left_val>
<right_val>0.8792119026184082</right_val></_></_>
<_>
<!-- tree 24 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
0 0 8 2 -1.</_>
<_>
0 0 4 1 2.</_>
<_>
4 1 4 1 2.</_></rects>
<tilted>0</tilted></feature>
<threshold>-4.2572239181026816e-05</threshold>
<left_val>1.</left_val>
<right_val>-1.</right_val></_></_>
<_>
<!-- tree 25 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
12 0 8 2 -1.</_>
<_>
16 0 4 1 2.</_>
<_>
12 1 4 1 2.</_></rects>
<tilted>0</tilted></feature>
<threshold>3.4698568924795836e-05</threshold>
<left_val>-0.8942371010780334</left_val>
<right_val>0.6385173201560974</right_val></_></_>
<_>
<!-- tree 26 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
1 0 13 15 -1.</_>
<_>
1 5 13 5 3.</_></rects>
<tilted>0</tilted></feature>
<threshold>6.0833231545984745e-03</threshold>
<left_val>-0.9911761283874512</left_val>
<right_val>0.8617964982986450</right_val></_></_>
<_>
<!-- tree 27 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
17 18 1 2 -1.</_>
<_>
17 19 1 1 2.</_></rects>
<tilted>0</tilted></feature>
<threshold>1.5569420065730810e-04</threshold>
<left_val>-1.</left_val>
<right_val>0.9989972114562988</right_val></_></_>
<_>
<!-- tree 28 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
0 0 4 3 -1.</_>
<_>
2 0 2 3 2.</_></rects>
<tilted>0</tilted></feature>
<threshold>0.</threshold>
<left_val>0.</left_val>
<right_val>-1.</right_val></_></_>
<_>
<!-- tree 29 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
9 19 4 1 -1.</_>
<_>
9 19 2 1 2.</_></rects>
<tilted>0</tilted></feature>
<threshold>5.8437039115233347e-05</threshold>
<left_val>-0.9401987791061401</left_val>
<right_val>0.9499294161796570</right_val></_></_>
<_>
<!-- tree 30 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
3 13 14 4 -1.</_>
<_>
3 15 14 2 2.</_></rects>
<tilted>0</tilted></feature>
<threshold>8.5243082139641047e-04</threshold>
<left_val>-1.</left_val>
<right_val>1.0000870227813721</right_val></_></_>
<_>
<!-- tree 31 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
17 0 3 4 -1.</_>
<_>
17 2 3 2 2.</_></rects>
<tilted>0</tilted></feature>
<threshold>0.</threshold>
<left_val>0.</left_val>
<right_val>-1.</right_val></_></_>
<_>
<!-- tree 32 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
7 1 2 3 -1.</_>
<_>
7 2 2 1 3.</_></rects>
<tilted>0</tilted></feature>
<threshold>8.8114888058044016e-05</threshold>
<left_val>-1.</left_val>
<right_val>1.0001029968261719</right_val></_></_>
<_>
<!-- tree 33 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
17 0 3 4 -1.</_>
<_>
17 2 3 2 2.</_></rects>
<tilted>0</tilted></feature>
<threshold>0.</threshold>
<left_val>0.</left_val>
<right_val>-1.</right_val></_></_>
<_>
<!-- tree 34 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
1 12 18 2 -1.</_>
<_>
7 12 6 2 3.</_></rects>
<tilted>0</tilted></feature>
<threshold>-1.6535379691049457e-03</threshold>
<left_val>0.9649471044540405</left_val>
<right_val>-0.9946994185447693</right_val></_></_>
<_>
<!-- tree 35 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
16 3 2 4 -1.</_>
<_>
17 3 1 2 2.</_>
<_>
16 5 1 2 2.</_></rects>
<tilted>0</tilted></feature>
<threshold>2.2355250257533044e-04</threshold>
<left_val>-0.8841317892074585</left_val>
<right_val>0.5885220170021057</right_val></_></_>
<_>
<!-- tree 36 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
3 13 10 2 -1.</_>
<_>
3 13 5 1 2.</_>
<_>
8 14 5 1 2.</_></rects>
<tilted>0</tilted></feature>
<threshold>-2.0420220680534840e-03</threshold>
<left_val>0.8850557208061218</left_val>
<right_val>-0.9887136220932007</right_val></_></_>
<_>
<!-- tree 37 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
11 13 6 2 -1.</_>
<_>
11 13 3 2 2.</_></rects>
<tilted>0</tilted></feature>
<threshold>-2.7822980191558599e-03</threshold>
<left_val>0.8021606206893921</left_val>
<right_val>-0.8011325001716614</right_val></_></_>
<_>
<!-- tree 38 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
6 4 6 12 -1.</_>
<_>
9 4 3 12 2.</_></rects>
<tilted>0</tilted></feature>
<threshold>2.6262819301337004e-03</threshold>
<left_val>-0.8629643917083740</left_val>
<right_val>0.9028394818305969</right_val></_></_>
<_>
<!-- tree 39 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
14 5 2 14 -1.</_>
<_>
15 5 1 7 2.</_>
<_>
14 12 1 7 2.</_></rects>
<tilted>0</tilted></feature>
<threshold>-5.8437039115233347e-05</threshold>
<left_val>0.5506380796432495</left_val>
<right_val>-0.8834760189056396</right_val></_></_>
<_>
<!-- tree 40 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
3 2 12 10 -1.</_>
<_>
9 2 6 10 2.</_></rects>
<tilted>0</tilted></feature>
<threshold>-1.1351429857313633e-03</threshold>
<left_val>0.9118285179138184</left_val>
<right_val>-0.8601468205451965</right_val></_></_>
<_>
<!-- tree 41 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
16 11 4 4 -1.</_>
<_>
16 13 4 2 2.</_></rects>
<tilted>0</tilted></feature>
<threshold>6.5544509561732411e-04</threshold>
<left_val>-0.5529929995536804</left_val>
<right_val>0.6181765794754028</right_val></_></_>
<_>
<!-- tree 42 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
5 19 10 1 -1.</_>
<_>
10 19 5 1 2.</_></rects>
<tilted>0</tilted></feature>
<threshold>3.8200760172912851e-05</threshold>
<left_val>-0.8676869273185730</left_val>
<right_val>0.7274010777473450</right_val></_></_>
<_>
<!-- tree 43 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
15 2 1 18 -1.</_>
<_>
15 11 1 9 2.</_></rects>
<tilted>0</tilted></feature>
<threshold>-6.2933329900261015e-05</threshold>
<left_val>0.3377492129802704</left_val>
<right_val>-0.8335667848587036</right_val></_></_>
<_>
<!-- tree 44 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
1 4 5 16 -1.</_>
<_>
1 12 5 8 2.</_></rects>
<tilted>0</tilted></feature>
<threshold>2.8638119692914188e-04</threshold>
<left_val>-0.8729416131973267</left_val>
<right_val>0.7917960286140442</right_val></_></_>
<_>
<!-- tree 45 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
7 6 12 6 -1.</_>
<_>
7 8 12 2 3.</_></rects>
<tilted>0</tilted></feature>
<threshold>3.6316178739070892e-04</threshold>
<left_val>-0.9013931751251221</left_val>
<right_val>0.7772005200386047</right_val></_></_>
<_>
<!-- tree 46 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
2 11 12 6 -1.</_>
<_>
2 11 6 3 2.</_>
<_>
8 14 6 3 2.</_></rects>
<tilted>0</tilted></feature>
<threshold>1.2007999466732144e-03</threshold>
<left_val>-0.9860498905181885</left_val>
<right_val>0.8049355149269104</right_val></_></_>
<_>
<!-- tree 47 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
6 0 14 18 -1.</_>
<_>
6 6 14 6 3.</_></rects>
<tilted>0</tilted></feature>
<threshold>-2.3152970243245363e-03</threshold>
<left_val>1.</left_val>
<right_val>-1.</right_val></_></_>
<_>
<!-- tree 48 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
0 0 19 18 -1.</_>
<_>
0 6 19 6 3.</_></rects>
<tilted>0</tilted></feature>
<threshold>0.0144739197567105</threshold>
<left_val>-0.9682086706161499</left_val>
<right_val>0.9563586115837097</right_val></_></_>
<_>
<!-- tree 49 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
10 17 1 3 -1.</_>
<_>
10 18 1 1 3.</_></rects>
<tilted>0</tilted></feature>
<threshold>-3.2585670705884695e-03</threshold>
<left_val>1.</left_val>
<right_val>-0.9941142201423645</right_val></_></_>
<_>
<!-- tree 50 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
2 10 5 10 -1.</_>
<_>
2 15 5 5 2.</_></rects>
<tilted>0</tilted></feature>
<threshold>0.0134088601917028</threshold>
<left_val>-0.9944000840187073</left_val>
<right_val>0.8795533776283264</right_val></_></_>
<_>
<!-- tree 51 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
17 0 3 1 -1.</_>
<_>
18 0 1 1 3.</_></rects>
<tilted>0</tilted></feature>
<threshold>4.0174949390348047e-05</threshold>
<left_val>-0.9955059885978699</left_val>
<right_val>0.4559975862503052</right_val></_></_>
<_>
<!-- tree 52 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
0 16 5 3 -1.</_>
<_>
0 17 5 1 3.</_></rects>
<tilted>0</tilted></feature>
<threshold>1.8752219330053777e-04</threshold>
<left_val>-1.</left_val>
<right_val>1.0003039836883545</right_val></_></_>
<_>
<!-- tree 53 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
19 0 1 2 -1.</_>
<_>
19 1 1 1 2.</_></rects>
<tilted>0</tilted></feature>
<threshold>0.</threshold>
<left_val>0.</left_val>
<right_val>-1.</right_val></_></_>
<_>
<!-- tree 54 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
0 12 14 1 -1.</_>
<_>
7 12 7 1 2.</_></rects>
<tilted>0</tilted></feature>
<threshold>-5.7442798279225826e-03</threshold>
<left_val>1.</left_val>
<right_val>-1.</right_val></_></_>
<_>
<!-- tree 55 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
13 12 6 6 -1.</_>
<_>
13 14 6 2 3.</_></rects>
<tilted>0</tilted></feature>
<threshold>2.8128331177867949e-04</threshold>
<left_val>-0.9679043292999268</left_val>
<right_val>0.5377150774002075</right_val></_></_>
<_>
<!-- tree 56 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
0 11 4 4 -1.</_>
<_>
0 13 4 2 2.</_></rects>
<tilted>0</tilted></feature>
<threshold>2.9258249560371041e-04</threshold>
<left_val>-0.9925985932350159</left_val>
<right_val>0.7377948760986328</right_val></_></_>
<_>
<!-- tree 57 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
10 17 3 3 -1.</_>
<_>
10 18 3 1 3.</_></rects>
<tilted>0</tilted></feature>
<threshold>-7.6873782090842724e-03</threshold>
<left_val>0.4390138089656830</left_val>
<right_val>-0.9956768155097961</right_val></_></_>
<_>
<!-- tree 58 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
2 10 15 5 -1.</_>
<_>
7 10 5 5 3.</_></rects>
<tilted>0</tilted></feature>
<threshold>-1.6997690545395017e-04</threshold>
<left_val>0.8890876173973083</left_val>
<right_val>-0.9900755286216736</right_val></_></_>
<_>
<!-- tree 59 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
14 9 1 4 -1.</_>
<_>
14 11 1 2 2.</_></rects>
<tilted>0</tilted></feature>
<threshold>-2.8665470381383784e-05</threshold>
<left_val>0.4759410917758942</left_val>
<right_val>-0.9352231025695801</right_val></_></_>
<_>
<!-- tree 60 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
5 9 6 4 -1.</_>
<_>
5 9 3 2 2.</_>
<_>
8 11 3 2 2.</_></rects>
<tilted>0</tilted></feature>
<threshold>4.4182338751852512e-04</threshold>
<left_val>-0.7511792182922363</left_val>
<right_val>0.8805574178695679</right_val></_></_></trees>
<stage_threshold>-4.9593520164489746</stage_threshold>
<parent>2</parent>
<next>-1</next></_>
<_>
<!-- stage 4 -->
<trees>
<_>
<!-- tree 0 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
0 3 14 14 -1.</_>
<_>
0 3 7 7 2.</_>
<_>
7 10 7 7 2.</_></rects>
<tilted>0</tilted></feature>
<threshold>-0.0127300098538399</threshold>
<left_val>0.4832380115985870</left_val>
<right_val>-0.7198603749275208</right_val></_></_>
<_>
<!-- tree 1 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
0 2 20 8 -1.</_>
<_>
0 6 20 4 2.</_></rects>
<tilted>0</tilted></feature>
<threshold>0.0589522011578083</threshold>
<left_val>-0.4658026993274689</left_val>
<right_val>0.4875808060169220</right_val></_></_>
<_>
<!-- tree 2 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
0 12 8 8 -1.</_>
<_>
0 16 8 4 2.</_></rects>
<tilted>0</tilted></feature>
<threshold>7.8740529716014862e-04</threshold>
<left_val>-0.7789018750190735</left_val>
<right_val>0.2557401061058044</right_val></_></_>
<_>
<!-- tree 3 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
7 12 6 6 -1.</_>
<_>
7 14 6 2 3.</_></rects>
<tilted>0</tilted></feature>
<threshold>0.0105524603277445</threshold>
<left_val>-0.6375812888145447</left_val>
<right_val>0.3461680114269257</right_val></_></_>
<_>
<!-- tree 4 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
1 18 8 2 -1.</_>
<_>
1 18 4 1 2.</_>
<_>
5 19 4 1 2.</_></rects>
<tilted>0</tilted></feature>
<threshold>8.0834580585360527e-03</threshold>
<left_val>-0.6557192206382751</left_val>
<right_val>0.6636518239974976</right_val></_></_>
<_>
<!-- tree 5 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
8 10 4 8 -1.</_>
<_>
8 14 4 4 2.</_></rects>
<tilted>0</tilted></feature>
<threshold>0.0235214307904243</threshold>
<left_val>-0.9006652832031250</left_val>
<right_val>0.4957715868949890</right_val></_></_>
<_>
<!-- tree 6 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
0 12 6 5 -1.</_>
<_>
2 12 2 5 3.</_></rects>
<tilted>0</tilted></feature>
<threshold>2.1901269792579114e-04</threshold>
<left_val>-0.9414082765579224</left_val>
<right_val>0.4645870029926300</right_val></_></_>
<_>
<!-- tree 7 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
10 8 9 12 -1.</_>
<_>
10 12 9 4 3.</_></rects>
<tilted>0</tilted></feature>
<threshold>-1.5295119374059141e-04</threshold>
<left_val>0.1733245998620987</left_val>
<right_val>-0.9518421888351440</right_val></_></_>
<_>
<!-- tree 8 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
5 5 10 15 -1.</_>
<_>
5 10 10 5 3.</_></rects>
<tilted>0</tilted></feature>
<threshold>-4.9944370985031128e-03</threshold>
<left_val>0.2332555055618286</left_val>
<right_val>-0.9303036928176880</right_val></_></_>
<_>
<!-- tree 9 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
1 2 18 14 -1.</_>
<_>
10 2 9 7 2.</_>
<_>
1 9 9 7 2.</_></rects>
<tilted>0</tilted></feature>
<threshold>-2.8488549869507551e-03</threshold>
<left_val>0.5224574208259583</left_val>
<right_val>-0.6394140124320984</right_val></_></_>
<_>
<!-- tree 10 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
2 3 3 16 -1.</_>
<_>
2 11 3 8 2.</_></rects>
<tilted>0</tilted></feature>
<threshold>8.3920639008283615e-03</threshold>
<left_val>-0.6068183183670044</left_val>
<right_val>0.4723689854145050</right_val></_></_>
<_>
<!-- tree 11 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
6 17 13 3 -1.</_>
<_>
6 18 13 1 3.</_></rects>
<tilted>0</tilted></feature>
<threshold>-3.5511489841155708e-05</threshold>
<left_val>0.2968985140323639</left_val>
<right_val>-0.6452224850654602</right_val></_></_>
<_>
<!-- tree 12 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
5 11 9 3 -1.</_>
<_>
8 11 3 3 3.</_></rects>
<tilted>0</tilted></feature>
<threshold>2.1621841005980968e-03</threshold>
<left_val>-0.4258666932582855</left_val>
<right_val>0.5548338890075684</right_val></_></_>
<_>
<!-- tree 13 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
1 12 18 4 -1.</_>
<_>
7 12 6 4 3.</_></rects>
<tilted>0</tilted></feature>
<threshold>-5.1551498472690582e-03</threshold>
<left_val>0.3051683902740479</left_val>
<right_val>-0.8206862807273865</right_val></_></_>
<_>
<!-- tree 14 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
3 9 4 2 -1.</_>
<_>
3 9 2 1 2.</_>
<_>
5 10 2 1 2.</_></rects>
<tilted>0</tilted></feature>
<threshold>1.7603079322725534e-04</threshold>
<left_val>-0.4252283871173859</left_val>
<right_val>0.4734784960746765</right_val></_></_>
<_>
<!-- tree 15 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
7 3 8 3 -1.</_>
<_>
7 4 8 1 3.</_></rects>
<tilted>0</tilted></feature>
<threshold>-5.6310528889298439e-03</threshold>
<left_val>0.4430184960365295</left_val>
<right_val>-0.5268139839172363</right_val></_></_>
<_>
<!-- tree 16 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
0 17 2 3 -1.</_>
<_>
0 18 2 1 3.</_></rects>
<tilted>0</tilted></feature>
<threshold>1.0609399760141969e-04</threshold>
<left_val>-0.4128456115722656</left_val>
<right_val>0.4862971007823944</right_val></_></_>
<_>
<!-- tree 17 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
5 8 10 4 -1.</_>
<_>
5 10 10 2 2.</_></rects>
<tilted>0</tilted></feature>
<threshold>-0.0146872196346521</threshold>
<left_val>0.3483710885047913</left_val>
<right_val>-0.6565722227096558</right_val></_></_>
<_>
<!-- tree 18 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
1 12 15 6 -1.</_>
<_>
1 14 15 2 3.</_></rects>
<tilted>0</tilted></feature>
<threshold>0.0810066536068916</threshold>
<left_val>-0.3347136080265045</left_val>
<right_val>0.6498758792877197</right_val></_></_>
<_>
<!-- tree 19 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
6 19 14 1 -1.</_>
<_>
6 19 7 1 2.</_></rects>
<tilted>0</tilted></feature>
<threshold>7.1147878770716488e-05</threshold>
<left_val>-0.5422406792640686</left_val>
<right_val>0.2807042896747589</right_val></_></_>
<_>
<!-- tree 20 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
0 19 16 1 -1.</_>
<_>
8 19 8 1 2.</_></rects>
<tilted>0</tilted></feature>
<threshold>2.6208710551145487e-05</threshold>
<left_val>-0.7503160834312439</left_val>
<right_val>0.4175724089145660</right_val></_></_>
<_>
<!-- tree 21 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
14 11 1 2 -1.</_>
<_>
14 12 1 1 2.</_></rects>
<tilted>0</tilted></feature>
<threshold>-2.2025800717528909e-05</threshold>
<left_val>0.3986887931823730</left_val>
<right_val>-0.8484249711036682</right_val></_></_>
<_>
<!-- tree 22 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
3 11 3 2 -1.</_>
<_>
3 12 3 1 2.</_></rects>
<tilted>0</tilted></feature>
<threshold>-2.7908370611839928e-05</threshold>
<left_val>0.4262354969978333</left_val>
<right_val>-0.6090481281280518</right_val></_></_>
<_>
<!-- tree 23 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
5 12 12 1 -1.</_>
<_>
5 12 6 1 2.</_></rects>
<tilted>0</tilted></feature>
<threshold>-3.7988298572599888e-04</threshold>
<left_val>0.2306731045246124</left_val>
<right_val>-0.3030667901039124</right_val></_></_>
<_>
<!-- tree 24 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
3 12 12 1 -1.</_>
<_>
9 12 6 1 2.</_></rects>
<tilted>0</tilted></feature>
<threshold>-2.8329479391686618e-05</threshold>
<left_val>0.4294688999652863</left_val>
<right_val>-0.6150280237197876</right_val></_></_></trees>
<stage_threshold>-2.0059499740600586</stage_threshold>
<parent>3</parent>
<next>-1</next></_>
<_>
<!-- stage 5 -->
<trees>
<_>
<!-- tree 0 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
7 18 3 2 -1.</_>
<_>
8 18 1 2 3.</_></rects>
<tilted>0</tilted></feature>
<threshold>-8.7926961714401841e-04</threshold>
<left_val>-0.8508998155593872</left_val>
<right_val>0.2012203931808472</right_val></_></_>
<_>
<!-- tree 1 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
10 18 3 2 -1.</_>
<_>
11 18 1 2 3.</_></rects>
<tilted>0</tilted></feature>
<threshold>-1.0719529818743467e-03</threshold>
<left_val>-0.8750498294830322</left_val>
<right_val>0.1188623011112213</right_val></_></_>
<_>
<!-- tree 2 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
7 18 3 2 -1.</_>
<_>
8 18 1 2 3.</_></rects>
<tilted>0</tilted></feature>
<threshold>1.1958930408582091e-03</threshold>
<left_val>0.1821606010198593</left_val>
<right_val>-0.8673701882362366</right_val></_></_>
<_>
<!-- tree 3 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
4 1 13 6 -1.</_>
<_>
4 3 13 2 3.</_></rects>
<tilted>0</tilted></feature>
<threshold>-0.0367217697203159</threshold>
<left_val>0.3615708947181702</left_val>
<right_val>-0.3918508887290955</right_val></_></_>
<_>
<!-- tree 4 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
8 15 2 1 -1.</_>
<_>
9 15 1 1 2.</_></rects>
<tilted>0</tilted></feature>
<threshold>2.8816348640248179e-04</threshold>
<left_val>0.1872649937868118</left_val>
<right_val>-0.7076212763786316</right_val></_></_>
<_>
<!-- tree 5 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
10 15 3 1 -1.</_>
<_>
11 15 1 1 3.</_></rects>
<tilted>0</tilted></feature>
<threshold>6.8340590223670006e-04</threshold>
<left_val>0.1269242018461227</left_val>
<right_val>-0.7228708863258362</right_val></_></_>
<_>
<!-- tree 6 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
1 12 18 1 -1.</_>
<_>
7 12 6 1 3.</_></rects>
<tilted>0</tilted></feature>
<threshold>-0.0425732918083668</threshold>
<left_val>0.5858349800109863</left_val>
<right_val>-0.2147608995437622</right_val></_></_></trees>
<stage_threshold>-0.9255558848381042</stage_threshold>
<parent>4</parent>
<next>-1</next></_>
<_>
<!-- stage 6 -->
<trees>
<_>
<!-- tree 0 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
6 18 7 2 -1.</_>
<_>
6 19 7 1 2.</_></rects>
<tilted>0</tilted></feature>
<threshold>0.0233492702245712</threshold>
<left_val>-0.2366411983966827</left_val>
<right_val>0.5849282145500183</right_val></_></_>
<_>
<!-- tree 1 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
12 16 2 1 -1.</_>
<_>
12 16 1 1 2.</_></rects>
<tilted>0</tilted></feature>
<threshold>4.9444608157500625e-04</threshold>
<left_val>0.1428918987512589</left_val>
<right_val>-0.6820772290229797</right_val></_></_>
<_>
<!-- tree 2 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
3 8 4 6 -1.</_>
<_>
3 8 2 3 2.</_>
<_>
5 11 2 3 2.</_></rects>
<tilted>0</tilted></feature>
<threshold>-0.0177930891513824</threshold>
<left_val>0.5955523848533630</left_val>
<right_val>-0.2330096960067749</right_val></_></_>
<_>
<!-- tree 3 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
2 3 18 4 -1.</_>
<_>
2 5 18 2 2.</_></rects>
<tilted>0</tilted></feature>
<threshold>0.0353034809231758</threshold>
<left_val>-0.3556973040103912</left_val>
<right_val>0.3598164916038513</right_val></_></_>
<_>
<!-- tree 4 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
6 16 2 2 -1.</_>
<_>
7 16 1 2 2.</_></rects>
<tilted>0</tilted></feature>
<threshold>7.1409897645935416e-04</threshold>
<left_val>0.1659422963857651</left_val>
<right_val>-0.7856965065002441</right_val></_></_>
<_>
<!-- tree 5 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
9 19 2 1 -1.</_>
<_>
9 19 1 1 2.</_></rects>
<tilted>0</tilted></feature>
<threshold>-3.5466518602333963e-04</threshold>
<left_val>-0.7188175916671753</left_val>
<right_val>0.1491793990135193</right_val></_></_>
<_>
<!-- tree 6 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
9 19 2 1 -1.</_>
<_>
10 19 1 1 2.</_></rects>
<tilted>0</tilted></feature>
<threshold>-3.2956211362034082e-04</threshold>
<left_val>-0.7239602804183960</left_val>
<right_val>0.1283237040042877</right_val></_></_>
<_>
<!-- tree 7 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
1 12 18 3 -1.</_>
<_>
7 12 6 3 3.</_></rects>
<tilted>0</tilted></feature>
<threshold>-0.0558854192495346</threshold>
<left_val>0.2699365019798279</left_val>
<right_val>-0.3814569115638733</right_val></_></_>
<_>
<!-- tree 8 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
5 8 10 9 -1.</_>
<_>
5 11 10 3 3.</_></rects>
<tilted>0</tilted></feature>
<threshold>-0.2315281033515930</threshold>
<left_val>0.5102406740188599</left_val>
<right_val>-0.2150623947381973</right_val></_></_>
<_>
<!-- tree 9 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
7 0 6 18 -1.</_>
<_>
9 0 2 18 3.</_></rects>
<tilted>0</tilted></feature>
<threshold>3.8320471066981554e-03</threshold>
<left_val>-0.3187570869922638</left_val>
<right_val>0.3741405010223389</right_val></_></_>
<_>
<!-- tree 10 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
2 5 8 4 -1.</_>
<_>
2 5 4 2 2.</_>
<_>
6 7 4 2 2.</_></rects>
<tilted>0</tilted></feature>
<threshold>-7.1148001588881016e-03</threshold>
<left_val>0.3868972063064575</left_val>
<right_val>-0.3064059019088745</right_val></_></_>
<_>
<!-- tree 11 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
13 11 2 3 -1.</_>
<_>
13 11 1 3 2.</_></rects>
<tilted>0</tilted></feature>
<threshold>1.0463730432093143e-03</threshold>
<left_val>-0.0578359216451645</left_val>
<right_val>0.2854403853416443</right_val></_></_>
<_>
<!-- tree 12 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
5 11 2 3 -1.</_>
<_>
6 11 1 3 2.</_></rects>
<tilted>0</tilted></feature>
<threshold>1.2736029748339206e-04</threshold>
<left_val>-0.3159281015396118</left_val>
<right_val>0.4068993926048279</right_val></_></_></trees>
<stage_threshold>-1.1411540508270264</stage_threshold>
<parent>5</parent>
<next>-1</next></_>
<_>
<!-- stage 7 -->
<trees>
<_>
<!-- tree 0 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
1 19 18 1 -1.</_>
<_>
7 19 6 1 3.</_></rects>
<tilted>0</tilted></feature>
<threshold>0.0220439601689577</threshold>
<left_val>-0.2536872923374176</left_val>
<right_val>0.5212177038192749</right_val></_></_>
<_>
<!-- tree 1 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
12 14 3 6 -1.</_>
<_>
13 14 1 6 3.</_></rects>
<tilted>0</tilted></feature>
<threshold>2.1312560420483351e-03</threshold>
<left_val>0.1482914984226227</left_val>
<right_val>-0.5914195775985718</right_val></_></_>
<_>
<!-- tree 2 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
0 11 12 4 -1.</_>
<_>
4 11 4 4 3.</_></rects>
<tilted>0</tilted></feature>
<threshold>-0.0413990207016468</threshold>
<left_val>0.4204145073890686</left_val>
<right_val>-0.2349137067794800</right_val></_></_>
<_>
<!-- tree 3 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
0 2 20 8 -1.</_>
<_>
0 6 20 4 2.</_></rects>
<tilted>0</tilted></feature>
<threshold>0.1522327959537506</threshold>
<left_val>-0.3104422092437744</left_val>
<right_val>0.4176956117153168</right_val></_></_>
<_>
<!-- tree 4 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
7 14 2 4 -1.</_>
<_>
8 14 1 4 2.</_></rects>
<tilted>0</tilted></feature>
<threshold>7.2278419975191355e-04</threshold>
<left_val>0.2251144051551819</left_val>
<right_val>-0.6049224138259888</right_val></_></_>
<_>
<!-- tree 5 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
5 10 10 8 -1.</_>
<_>
10 10 5 4 2.</_>
<_>
5 14 5 4 2.</_></rects>
<tilted>0</tilted></feature>
<threshold>0.0139188598841429</threshold>
<left_val>0.1998808979988098</left_val>
<right_val>-0.5362910032272339</right_val></_></_>
<_>
<!-- tree 6 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
5 12 1 4 -1.</_>
<_>
5 14 1 2 2.</_></rects>
<tilted>0</tilted></feature>
<threshold>9.3200067058205605e-03</threshold>
<left_val>-0.3086053133010864</left_val>
<right_val>0.3600850105285645</right_val></_></_>
<_>
<!-- tree 7 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
10 0 1 8 -1.</_>
<_>
10 4 1 4 2.</_></rects>
<tilted>0</tilted></feature>
<threshold>-0.0135594001039863</threshold>
<left_val>0.7699136137962341</left_val>
<right_val>-0.1129935979843140</right_val></_></_>
<_>
<!-- tree 8 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
1 8 18 8 -1.</_>
<_>
7 8 6 8 3.</_></rects>
<tilted>0</tilted></feature>
<threshold>-0.2024694979190826</threshold>
<left_val>0.5726454854011536</left_val>
<right_val>-0.1685701012611389</right_val></_></_>
<_>
<!-- tree 9 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
9 8 10 4 -1.</_>
<_>
9 8 5 4 2.</_></rects>
<tilted>0</tilted></feature>
<threshold>0.0256939493119717</threshold>
<left_val>-0.0890305936336517</left_val>
<right_val>0.4055748879909515</right_val></_></_>
<_>
<!-- tree 10 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
6 6 8 3 -1.</_>
<_>
6 7 8 1 3.</_></rects>
<tilted>0</tilted></feature>
<threshold>-0.0135868499055505</threshold>
<left_val>0.4805161952972412</left_val>
<right_val>-0.1680151969194412</right_val></_></_>
<_>
<!-- tree 11 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
10 9 3 3 -1.</_>
<_>
11 9 1 3 3.</_></rects>
<tilted>0</tilted></feature>
<threshold>-6.3351547578349710e-04</threshold>
<left_val>0.2068227976560593</left_val>
<right_val>-0.2571463882923126</right_val></_></_>
<_>
<!-- tree 12 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
4 14 2 4 -1.</_>
<_>
5 14 1 4 2.</_></rects>
<tilted>0</tilted></feature>
<threshold>1.3086969556752592e-04</threshold>
<left_val>0.2003916949033737</left_val>
<right_val>-0.4468185007572174</right_val></_></_>
<_>
<!-- tree 13 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
10 17 10 2 -1.</_>
<_>
15 17 5 1 2.</_>
<_>
10 18 5 1 2.</_></rects>
<tilted>0</tilted></feature>
<threshold>9.4451867043972015e-03</threshold>
<left_val>0.0453975386917591</left_val>
<right_val>-0.6604390144348145</right_val></_></_>
<_>
<!-- tree 14 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
3 18 3 2 -1.</_>
<_>
4 18 1 2 3.</_></rects>
<tilted>0</tilted></feature>
<threshold>-1.1732289567589760e-03</threshold>
<left_val>-0.7233589887619019</left_val>
<right_val>0.1189457029104233</right_val></_></_>
<_>
<!-- tree 15 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
13 2 4 9 -1.</_>
<_>
13 2 2 9 2.</_></rects>
<tilted>0</tilted></feature>
<threshold>-0.0270948894321918</threshold>
<left_val>0.4183718860149384</left_val>
<right_val>-0.0622722618281841</right_val></_></_>
<_>
<!-- tree 16 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
3 2 4 9 -1.</_>
<_>
5 2 2 9 2.</_></rects>
<tilted>0</tilted></feature>
<threshold>0.0128746498376131</threshold>
<left_val>-0.2036883980035782</left_val>
<right_val>0.4376415908336639</right_val></_></_>
<_>
<!-- tree 17 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
9 8 2 8 -1.</_>
<_>
10 8 1 4 2.</_>
<_>
9 12 1 4 2.</_></rects>
<tilted>0</tilted></feature>
<threshold>-2.8124409727752209e-03</threshold>
<left_val>-0.6812670230865479</left_val>
<right_val>0.1294167041778564</right_val></_></_></trees>
<stage_threshold>-1.2025229930877686</stage_threshold>
<parent>6</parent>
<next>-1</next></_>
<_>
<!-- stage 8 -->
<trees>
<_>
<!-- tree 0 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
0 18 14 2 -1.</_>
<_>
0 18 7 1 2.</_>
<_>
7 19 7 1 2.</_></rects>
<tilted>0</tilted></feature>
<threshold>0.0179104395210743</threshold>
<left_val>-0.2364671975374222</left_val>
<right_val>0.5514438152313232</right_val></_></_>
<_>
<!-- tree 1 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
10 13 9 1 -1.</_>
<_>
13 13 3 1 3.</_></rects>
<tilted>0</tilted></feature>
<threshold>-5.0143511034548283e-03</threshold>
<left_val>0.4693753123283386</left_val>
<right_val>-0.3883568942546844</right_val></_></_>
<_>
<!-- tree 2 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
6 15 3 1 -1.</_>
<_>
7 15 1 1 3.</_></rects>
<tilted>0</tilted></feature>
<threshold>4.2181540629826486e-04</threshold>
<left_val>0.1153784990310669</left_val>
<right_val>-0.7132592797279358</right_val></_></_>
<_>
<!-- tree 3 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
0 16 20 4 -1.</_>
<_>
10 16 10 2 2.</_>
<_>
0 18 10 2 2.</_></rects>
<tilted>0</tilted></feature>
<threshold>-0.0263313204050064</threshold>
<left_val>-0.6675789952278137</left_val>
<right_val>0.1828629970550537</right_val></_></_>
<_>
<!-- tree 4 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
1 13 18 4 -1.</_>
<_>
1 13 9 2 2.</_>
<_>
10 15 9 2 2.</_></rects>
<tilted>0</tilted></feature>
<threshold>0.0270899794995785</threshold>
<left_val>0.0714882835745811</left_val>
<right_val>-0.7389600276947021</right_val></_></_>
<_>
<!-- tree 5 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
10 10 6 1 -1.</_>
<_>
12 10 2 1 3.</_></rects>
<tilted>0</tilted></feature>
<threshold>3.9808810688555241e-03</threshold>
<left_val>-0.0624900311231613</left_val>
<right_val>0.2579961121082306</right_val></_></_>
<_>
<!-- tree 6 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
0 10 12 6 -1.</_>
<_>
4 10 4 6 3.</_></rects>
<tilted>0</tilted></feature>
<threshold>0.0938581079244614</threshold>
<left_val>-0.1166857033967972</left_val>
<right_val>0.8323975801467896</right_val></_></_>
<_>
<!-- tree 7 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
10 11 9 4 -1.</_>
<_>
13 11 3 4 3.</_></rects>
<tilted>0</tilted></feature>
<threshold>-0.0170704908668995</threshold>
<left_val>0.2551425099372864</left_val>
<right_val>-0.1464619040489197</right_val></_></_>
<_>
<!-- tree 8 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
1 13 9 1 -1.</_>
<_>
4 13 3 1 3.</_></rects>
<tilted>0</tilted></feature>
<threshold>-5.6102341040968895e-03</threshold>
<left_val>0.3810698091983795</left_val>
<right_val>-0.2898282110691071</right_val></_></_>
<_>
<!-- tree 9 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
12 17 1 3 -1.</_>
<_>
12 18 1 1 3.</_></rects>
<tilted>0</tilted></feature>
<threshold>-1.6884109936654568e-03</threshold>
<left_val>0.3976930975914001</left_val>
<right_val>-0.1791553944349289</right_val></_></_>
<_>
<!-- tree 10 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
5 17 3 3 -1.</_>
<_>
6 17 1 3 3.</_></rects>
<tilted>0</tilted></feature>
<threshold>1.1422219686210155e-03</threshold>
<left_val>0.1220583021640778</left_val>
<right_val>-0.7954893708229065</right_val></_></_>
<_>
<!-- tree 11 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
0 2 20 8 -1.</_>
<_>
0 6 20 4 2.</_></rects>
<tilted>0</tilted></feature>
<threshold>0.0854484736919403</threshold>
<left_val>-0.3227156102657318</left_val>
<right_val>0.2583124935626984</right_val></_></_></trees>
<stage_threshold>-0.8488889932632446</stage_threshold>
<parent>7</parent>
<next>-1</next></_>
<_>
<!-- stage 9 -->
<trees>
<_>
<!-- tree 0 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
5 12 1 6 -1.</_>
<_>
5 15 1 3 2.</_></rects>
<tilted>0</tilted></feature>
<threshold>-1.2407209724187851e-03</threshold>
<left_val>0.7162470817565918</left_val>
<right_val>-0.2007752954959869</right_val></_></_>
<_>
<!-- tree 1 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
6 5 14 10 -1.</_>
<_>
13 5 7 5 2.</_>
<_>
6 10 7 5 2.</_></rects>
<tilted>0</tilted></feature>
<threshold>-0.0822703167796135</threshold>
<left_val>0.3968873023986816</left_val>
<right_val>-0.2290832996368408</right_val></_></_>
<_>
<!-- tree 2 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
2 9 9 1 -1.</_>
<_>
5 9 3 1 3.</_></rects>
<tilted>0</tilted></feature>
<threshold>6.2309550121426582e-03</threshold>
<left_val>-0.2406931966543198</left_val>
<right_val>0.3659430146217346</right_val></_></_>
<_>
<!-- tree 3 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
10 11 9 3 -1.</_>
<_>
13 11 3 3 3.</_></rects>
<tilted>0</tilted></feature>
<threshold>-0.0140555696561933</threshold>
<left_val>0.2607584893703461</left_val>
<right_val>-0.2829737067222595</right_val></_></_>
<_>
<!-- tree 4 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
7 14 6 1 -1.</_>
<_>
9 14 2 1 3.</_></rects>
<tilted>0</tilted></feature>
<threshold>6.5327459014952183e-04</threshold>
<left_val>0.1528156995773315</left_val>
<right_val>-0.5593969821929932</right_val></_></_>
<_>
<!-- tree 5 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
19 0 1 16 -1.</_>
<_>
19 8 1 8 2.</_></rects>
<tilted>0</tilted></feature>
<threshold>0.0125494198873639</threshold>
<left_val>-0.2089716047048569</left_val>
<right_val>0.2781802117824554</right_val></_></_>
<_>
<!-- tree 6 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
7 4 6 10 -1.</_>
<_>
7 4 3 5 2.</_>
<_>
10 9 3 5 2.</_></rects>
<tilted>0</tilted></feature>
<threshold>0.0156330708414316</threshold>
<left_val>0.1483357995748520</left_val>
<right_val>-0.6003684997558594</right_val></_></_>
<_>
<!-- tree 7 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
10 9 2 3 -1.</_>
<_>
10 9 1 3 2.</_></rects>
<tilted>0</tilted></feature>
<threshold>7.4582709930837154e-04</threshold>
<left_val>-0.2270790934562683</left_val>
<right_val>0.1987556070089340</right_val></_></_>
<_>
<!-- tree 8 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
0 12 12 2 -1.</_>
<_>
4 12 4 2 3.</_></rects>
<tilted>0</tilted></feature>
<threshold>-0.0158222708851099</threshold>
<left_val>0.2820397913455963</left_val>
<right_val>-0.2920896112918854</right_val></_></_>
<_>
<!-- tree 9 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
12 18 3 2 -1.</_>
<_>
12 19 3 1 2.</_></rects>
<tilted>0</tilted></feature>
<threshold>8.7247788906097412e-03</threshold>
<left_val>-0.1720713973045349</left_val>
<right_val>0.4697273969650269</right_val></_></_>
<_>
<!-- tree 10 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
5 17 1 2 -1.</_>
<_>
5 18 1 1 2.</_></rects>
<tilted>0</tilted></feature>
<threshold>6.8489677505567670e-04</threshold>
<left_val>0.1544692963361740</left_val>
<right_val>-0.6636797189712524</right_val></_></_>
<_>
<!-- tree 11 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
9 11 2 1 -1.</_>
<_>
9 11 1 1 2.</_></rects>
<tilted>0</tilted></feature>
<threshold>2.5823758915066719e-04</threshold>
<left_val>0.1690579950809479</left_val>
<right_val>-0.4210532009601593</right_val></_></_>
<_>
<!-- tree 12 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
5 0 9 4 -1.</_>
<_>
8 0 3 4 3.</_></rects>
<tilted>0</tilted></feature>
<threshold>0.0420489497482777</threshold>
<left_val>-0.1286004930734634</left_val>
<right_val>0.6025344729423523</right_val></_></_>
<_>
<!-- tree 13 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
7 11 7 3 -1.</_>
<_>
7 12 7 1 3.</_></rects>
<tilted>0</tilted></feature>
<threshold>-0.0152104198932648</threshold>
<left_val>0.3247380852699280</left_val>
<right_val>-0.2400044947862625</right_val></_></_>
<_>
<!-- tree 14 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
8 14 3 1 -1.</_>
<_>
9 14 1 1 3.</_></rects>
<tilted>0</tilted></feature>
<threshold>-7.4586068512871861e-04</threshold>
<left_val>-0.7052754759788513</left_val>
<right_val>0.1198176965117455</right_val></_></_>
<_>
<!-- tree 15 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
7 9 6 4 -1.</_>
<_>
10 9 3 2 2.</_>
<_>
7 11 3 2 2.</_></rects>
<tilted>0</tilted></feature>
<threshold>-5.6090662255883217e-03</threshold>
<left_val>-0.5189142227172852</left_val>
<right_val>0.1511954963207245</right_val></_></_>
<_>
<!-- tree 16 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
7 9 3 3 -1.</_>
<_>
8 9 1 3 3.</_></rects>
<tilted>0</tilted></feature>
<threshold>-6.9692882243543863e-04</threshold>
<left_val>0.2492880970239639</left_val>
<right_val>-0.2738071978092194</right_val></_></_>
<_>
<!-- tree 17 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
9 9 2 1 -1.</_>
<_>
9 9 1 1 2.</_></rects>
<tilted>0</tilted></feature>
<threshold>-1.3032859424129128e-03</threshold>
<left_val>-0.7021797895431519</left_val>
<right_val>0.1096538975834846</right_val></_></_></trees>
<stage_threshold>-1.0809509754180908</stage_threshold>
<parent>8</parent>
<next>-1</next></_>
<_>
<!-- stage 10 -->
<trees>
<_>
<!-- tree 0 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
1 19 15 1 -1.</_>
<_>
6 19 5 1 3.</_></rects>
<tilted>0</tilted></feature>
<threshold>0.0127973603084683</threshold>
<left_val>-0.2490361928939819</left_val>
<right_val>0.4674673080444336</right_val></_></_>
<_>
<!-- tree 1 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
9 3 3 3 -1.</_>
<_>
9 4 3 1 3.</_></rects>
<tilted>0</tilted></feature>
<threshold>-4.1834129951894283e-03</threshold>
<left_val>0.3007251024246216</left_val>
<right_val>-0.2219883054494858</right_val></_></_>
<_>
<!-- tree 2 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
1 12 18 1 -1.</_>
<_>
7 12 6 1 3.</_></rects>
<tilted>0</tilted></feature>
<threshold>-0.0236128699034452</threshold>
<left_val>0.2414264976978302</left_val>
<right_val>-0.3374670147895813</right_val></_></_>
<_>
<!-- tree 3 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
14 8 1 9 -1.</_>
<_>
14 11 1 3 3.</_></rects>
<tilted>0</tilted></feature>
<threshold>-0.0251536108553410</threshold>
<left_val>0.4372070133686066</left_val>
<right_val>-0.3275614082813263</right_val></_></_>
<_>
<!-- tree 4 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
2 2 2 18 -1.</_>
<_>
2 11 2 9 2.</_></rects>
<tilted>0</tilted></feature>
<threshold>0.0211393106728792</threshold>
<left_val>-0.2863174080848694</left_val>
<right_val>0.3124063909053802</right_val></_></_>
<_>
<!-- tree 5 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
13 11 6 6 -1.</_>
<_>
16 11 3 3 2.</_>
<_>
13 14 3 3 2.</_></rects>
<tilted>0</tilted></feature>
<threshold>-0.0217125993221998</threshold>
<left_val>0.6942697763442993</left_val>
<right_val>-0.1012582033872604</right_val></_></_>
<_>
<!-- tree 6 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
1 9 18 6 -1.</_>
<_>
1 9 9 3 2.</_>
<_>
10 12 9 3 2.</_></rects>
<tilted>0</tilted></feature>
<threshold>-0.0430783592164516</threshold>
<left_val>-0.5607234239578247</left_val>
<right_val>0.1663125008344650</right_val></_></_>
<_>
<!-- tree 7 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
10 10 6 1 -1.</_>
<_>
12 10 2 1 3.</_></rects>
<tilted>0</tilted></feature>
<threshold>-1.4987450558692217e-03</threshold>
<left_val>0.1272646039724350</left_val>
<right_val>-0.1166080012917519</right_val></_></_>
<_>
<!-- tree 8 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
4 10 6 1 -1.</_>
<_>
6 10 2 1 3.</_></rects>
<tilted>0</tilted></feature>
<threshold>4.1716569103300571e-03</threshold>
<left_val>-0.2401334047317505</left_val>
<right_val>0.4614624083042145</right_val></_></_>
<_>
<!-- tree 9 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
17 13 3 7 -1.</_>
<_>
18 13 1 7 3.</_></rects>
<tilted>0</tilted></feature>
<threshold>4.8898528330028057e-03</threshold>
<left_val>0.0905465632677078</left_val>
<right_val>-0.4839006960391998</right_val></_></_>
<_>
<!-- tree 10 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
0 13 3 7 -1.</_>
<_>
1 13 1 7 3.</_></rects>
<tilted>0</tilted></feature>
<threshold>-1.1625960469245911e-03</threshold>
<left_val>-0.5429257154464722</left_val>
<right_val>0.1364106982946396</right_val></_></_>
<_>
<!-- tree 11 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
3 10 14 6 -1.</_>
<_>
10 10 7 3 2.</_>
<_>
3 13 7 3 2.</_></rects>
<tilted>0</tilted></feature>
<threshold>-0.0367816612124443</threshold>
<left_val>-0.7064548730850220</left_val>
<right_val>0.1088668033480644</right_val></_></_>
<_>
<!-- tree 12 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
1 10 6 5 -1.</_>
<_>
3 10 2 5 3.</_></rects>
<tilted>0</tilted></feature>
<threshold>0.0246897693723440</threshold>
<left_val>-0.1673354059457779</left_val>
<right_val>0.5149983167648315</right_val></_></_>
<_>
<!-- tree 13 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
9 7 2 3 -1.</_>
<_>
9 8 2 1 3.</_></rects>
<tilted>0</tilted></feature>
<threshold>-4.8654521815478802e-03</threshold>
<left_val>0.5060626268386841</left_val>
<right_val>-0.1594700068235397</right_val></_></_>
<_>
<!-- tree 14 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
5 8 10 3 -1.</_>
<_>
5 9 10 1 3.</_></rects>
<tilted>0</tilted></feature>
<threshold>-0.0117849996313453</threshold>
<left_val>0.4351908862590790</left_val>
<right_val>-0.1512733995914459</right_val></_></_>
<_>
<!-- tree 15 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
10 13 2 1 -1.</_>
<_>
10 13 1 1 2.</_></rects>
<tilted>0</tilted></feature>
<threshold>9.4989547505974770e-04</threshold>
<left_val>0.0692935213446617</left_val>
<right_val>-0.4393649101257324</right_val></_></_>
<_>
<!-- tree 16 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
8 13 2 1 -1.</_>
<_>
9 13 1 1 2.</_></rects>
<tilted>0</tilted></feature>
<threshold>5.9616740327328444e-04</threshold>
<left_val>0.0982565581798553</left_val>
<right_val>-0.6629868745803833</right_val></_></_>
<_>
<!-- tree 17 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
9 9 2 3 -1.</_>
<_>
9 10 2 1 3.</_></rects>
<tilted>0</tilted></feature>
<threshold>-6.2817288562655449e-03</threshold>
<left_val>0.4888150990009308</left_val>
<right_val>-0.1557238996028900</right_val></_></_></trees>
<stage_threshold>-1.1087180376052856</stage_threshold>
<parent>9</parent>
<next>-1</next></_>
<_>
<!-- stage 11 -->
<trees>
<_>
<!-- tree 0 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
9 0 1 8 -1.</_>
<_>
9 4 1 4 2.</_></rects>
<tilted>0</tilted></feature>
<threshold>-9.9095050245523453e-03</threshold>
<left_val>0.5630884766578674</left_val>
<right_val>-0.2063539028167725</right_val></_></_>
<_>
<!-- tree 1 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
19 0 1 14 -1.</_>
<_>
19 7 1 7 2.</_></rects>
<tilted>0</tilted></feature>
<threshold>4.5435219071805477e-03</threshold>
<left_val>-0.2470169961452484</left_val>
<right_val>0.1799020022153854</right_val></_></_>
<_>
<!-- tree 2 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
7 6 6 2 -1.</_>
<_>
7 7 6 1 2.</_></rects>
<tilted>0</tilted></feature>
<threshold>-8.7091082241386175e-04</threshold>
<left_val>0.2453050017356873</left_val>
<right_val>-0.2765454053878784</right_val></_></_>
<_>
<!-- tree 3 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
14 8 1 9 -1.</_>
<_>
14 11 1 3 3.</_></rects>
<tilted>0</tilted></feature>
<threshold>-0.0216368697583675</threshold>
<left_val>0.2515161931514740</left_val>
<right_val>-0.3227509856224060</right_val></_></_>
<_>
<!-- tree 4 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
2 18 4 2 -1.</_>
<_>
2 18 2 1 2.</_>
<_>
4 19 2 1 2.</_></rects>
<tilted>0</tilted></feature>
<threshold>2.5493409484624863e-03</threshold>
<left_val>-0.1476895958185196</left_val>
<right_val>0.5545899271965027</right_val></_></_>
<_>
<!-- tree 5 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
9 11 6 3 -1.</_>
<_>
9 11 3 3 2.</_></rects>
<tilted>0</tilted></feature>
<threshold>1.6613079933449626e-03</threshold>
<left_val>-0.2122790962457657</left_val>
<right_val>0.1571837961673737</right_val></_></_>
<_>
<!-- tree 6 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
0 0 1 14 -1.</_>
<_>
0 7 1 7 2.</_></rects>
<tilted>0</tilted></feature>
<threshold>9.4684818759560585e-03</threshold>
<left_val>-0.2621173858642578</left_val>
<right_val>0.2920702099800110</right_val></_></_>
<_>
<!-- tree 7 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
10 5 2 15 -1.</_>
<_>
10 10 2 5 3.</_></rects>
<tilted>0</tilted></feature>
<threshold>-0.0522385612130165</threshold>
<left_val>0.1780423969030380</left_val>
<right_val>-0.3343229889869690</right_val></_></_>
<_>
<!-- tree 8 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
5 11 6 3 -1.</_>
<_>
8 11 3 3 2.</_></rects>
<tilted>0</tilted></feature>
<threshold>2.5752868968993425e-03</threshold>
<left_val>-0.2065097987651825</left_val>
<right_val>0.4189889132976532</right_val></_></_>
<_>
<!-- tree 9 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
11 6 6 7 -1.</_>
<_>
13 6 2 7 3.</_></rects>
<tilted>0</tilted></feature>
<threshold>-0.0160471405833960</threshold>
<left_val>0.2585200071334839</left_val>
<right_val>-0.1094772964715958</right_val></_></_>
<_>
<!-- tree 10 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
4 10 12 9 -1.</_>
<_>
8 10 4 9 3.</_></rects>
<tilted>0</tilted></feature>
<threshold>-0.1159958988428116</threshold>
<left_val>0.6298483014106750</left_val>
<right_val>-0.1196947023272514</right_val></_></_>
<_>
<!-- tree 11 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
10 14 3 1 -1.</_>
<_>
11 14 1 1 3.</_></rects>
<tilted>0</tilted></feature>
<threshold>-9.7595580155029893e-04</threshold>
<left_val>-0.6507467031478882</left_val>
<right_val>0.0756275802850723</right_val></_></_>
<_>
<!-- tree 12 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
7 14 3 1 -1.</_>
<_>
8 14 1 1 3.</_></rects>
<tilted>0</tilted></feature>
<threshold>-4.2097578989341855e-04</threshold>
<left_val>-0.5833796858787537</left_val>
<right_val>0.1222841963171959</right_val></_></_>
<_>
<!-- tree 13 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
10 14 3 2 -1.</_>
<_>
11 14 1 2 3.</_></rects>
<tilted>0</tilted></feature>
<threshold>3.9017631206661463e-04</threshold>
<left_val>0.0758925378322601</left_val>
<right_val>-0.2629995942115784</right_val></_></_>
<_>
<!-- tree 14 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
4 8 2 6 -1.</_>
<_>
5 8 1 6 2.</_></rects>
<tilted>0</tilted></feature>
<threshold>3.1535029411315918e-03</threshold>
<left_val>-0.1664831042289734</left_val>
<right_val>0.4664255082607269</right_val></_></_>
<_>
<!-- tree 15 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
10 14 3 2 -1.</_>
<_>
11 14 1 2 3.</_></rects>
<tilted>0</tilted></feature>
<threshold>-1.4046890428289771e-03</threshold>
<left_val>-0.3981274962425232</left_val>
<right_val>0.0561619699001312</right_val></_></_>
<_>
<!-- tree 16 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
3 12 3 4 -1.</_>
<_>
4 12 1 4 3.</_></rects>
<tilted>0</tilted></feature>
<threshold>3.1666089780628681e-03</threshold>
<left_val>-0.1787768006324768</left_val>
<right_val>0.4090973138809204</right_val></_></_>
<_>
<!-- tree 17 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
3 1 14 6 -1.</_>
<_>
3 3 14 2 3.</_></rects>
<tilted>0</tilted></feature>
<threshold>-0.0164993591606617</threshold>
<left_val>0.2048030048608780</left_val>
<right_val>-0.3630825877189636</right_val></_></_>
<_>
<!-- tree 18 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
7 14 3 2 -1.</_>
<_>
8 14 1 2 3.</_></rects>
<tilted>0</tilted></feature>
<threshold>4.1761019383557141e-04</threshold>
<left_val>0.1311777979135513</left_val>
<right_val>-0.4833852946758270</right_val></_></_>
<_>
<!-- tree 19 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
12 11 3 3 -1.</_>
<_>
13 11 1 3 3.</_></rects>
<tilted>0</tilted></feature>
<threshold>9.0707670897245407e-03</threshold>
<left_val>9.2487707734107971e-03</left_val>
<right_val>-0.6447566151618958</right_val></_></_>
<_>
<!-- tree 20 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
5 11 3 3 -1.</_>
<_>
6 11 1 3 3.</_></rects>
<tilted>0</tilted></feature>
<threshold>3.3107338822446764e-04</threshold>
<left_val>-0.2549797892570496</left_val>
<right_val>0.2758406996726990</right_val></_></_>
<_>
<!-- tree 21 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
4 0 12 3 -1.</_>
<_>
4 1 12 1 3.</_></rects>
<tilted>0</tilted></feature>
<threshold>0.0139847695827484</threshold>
<left_val>0.1226134970784187</left_val>
<right_val>-0.5258917808532715</right_val></_></_>
<_>
<!-- tree 22 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
1 19 18 1 -1.</_>
<_>
7 19 6 1 3.</_></rects>
<tilted>0</tilted></feature>
<threshold>0.0238846298307180</threshold>
<left_val>-0.1637594997882843</left_val>
<right_val>0.3971964120864868</right_val></_></_>
<_>
<!-- tree 23 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
5 10 11 6 -1.</_>
<_>
5 12 11 2 3.</_></rects>
<tilted>0</tilted></feature>
<threshold>-0.0941136777400970</threshold>
<left_val>0.2231238931417465</left_val>
<right_val>-0.2817093133926392</right_val></_></_>
<_>
<!-- tree 24 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
0 9 12 1 -1.</_>
<_>
6 9 6 1 2.</_></rects>
<tilted>0</tilted></feature>
<threshold>-0.0163963604718447</threshold>
<left_val>0.5174812078475952</left_val>
<right_val>-0.1398597955703735</right_val></_></_></trees>
<stage_threshold>-1.1378910541534424</stage_threshold>
<parent>10</parent>
<next>-1</next></_>
<_>
<!-- stage 12 -->
<trees>
<_>
<!-- tree 0 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
5 12 1 6 -1.</_>
<_>
5 15 1 3 2.</_></rects>
<tilted>0</tilted></feature>
<threshold>-1.8984159396495670e-04</threshold>
<left_val>0.4796459972858429</left_val>
<right_val>-0.1926054060459137</right_val></_></_>
<_>
<!-- tree 1 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
14 12 6 6 -1.</_>
<_>
16 12 2 6 3.</_></rects>
<tilted>0</tilted></feature>
<threshold>4.7213290818035603e-03</threshold>
<left_val>-0.3855938911437988</left_val>
<right_val>0.2359178066253662</right_val></_></_>
<_>
<!-- tree 2 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
5 17 3 2 -1.</_>
<_>
5 18 3 1 2.</_></rects>
<tilted>0</tilted></feature>
<threshold>1.7611780203878880e-03</threshold>
<left_val>0.1145095974206924</left_val>
<right_val>-0.5536686778068542</right_val></_></_>
<_>
<!-- tree 3 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
14 12 6 6 -1.</_>
<_>
16 12 2 6 3.</_></rects>
<tilted>0</tilted></feature>
<threshold>0.0619058012962341</threshold>
<left_val>0.0361764803528786</left_val>
<right_val>-0.7537580132484436</right_val></_></_>
<_>
<!-- tree 4 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
0 12 6 6 -1.</_>
<_>
2 12 2 6 3.</_></rects>
<tilted>0</tilted></feature>
<threshold>6.8295709788799286e-03</threshold>
<left_val>-0.2995564043521881</left_val>
<right_val>0.2059424966573715</right_val></_></_>
<_>
<!-- tree 5 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
14 8 1 9 -1.</_>
<_>
14 11 1 3 3.</_></rects>
<tilted>0</tilted></feature>
<threshold>-0.0229486804455519</threshold>
<left_val>0.1910860985517502</left_val>
<right_val>-0.2746480107307434</right_val></_></_>
<_>
<!-- tree 6 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
0 16 11 4 -1.</_>
<_>
0 18 11 2 2.</_></rects>
<tilted>0</tilted></feature>
<threshold>0.0131213096901774</threshold>
<left_val>-0.1467829048633575</left_val>
<right_val>0.4494847953319550</right_val></_></_>
<_>
<!-- tree 7 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
14 8 1 9 -1.</_>
<_>
14 11 1 3 3.</_></rects>
<tilted>0</tilted></feature>
<threshold>-0.0331512987613678</threshold>
<left_val>0.2912957966327667</left_val>
<right_val>-0.1595291942358017</right_val></_></_>
<_>
<!-- tree 8 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
5 2 4 6 -1.</_>
<_>
5 5 4 3 2.</_></rects>
<tilted>0</tilted></feature>
<threshold>0.0224155597388744</threshold>
<left_val>-0.1776317954063416</left_val>
<right_val>0.3403505980968475</right_val></_></_>
<_>
<!-- tree 9 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
9 0 2 8 -1.</_>
<_>
9 4 2 4 2.</_></rects>
<tilted>0</tilted></feature>
<threshold>-0.0255698896944523</threshold>
<left_val>0.5480523109436035</left_val>
<right_val>-0.1752621978521347</right_val></_></_>
<_>
<!-- tree 10 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
8 10 2 8 -1.</_>
<_>
8 14 2 4 2.</_></rects>
<tilted>0</tilted></feature>
<threshold>0.0174023006111383</threshold>
<left_val>-0.3940981030464172</left_val>
<right_val>0.1953804939985275</right_val></_></_>
<_>
<!-- tree 11 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
12 12 8 3 -1.</_>
<_>
12 12 4 3 2.</_></rects>
<tilted>0</tilted></feature>
<threshold>-6.6808518022298813e-03</threshold>
<left_val>0.1267247051000595</left_val>
<right_val>-0.3698250055313110</right_val></_></_>
<_>
<!-- tree 12 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
1 3 18 3 -1.</_>
<_>
7 3 6 3 3.</_></rects>
<tilted>0</tilted></feature>
<threshold>-0.0474075004458427</threshold>
<left_val>-0.6734154224395752</left_val>
<right_val>0.0941268503665924</right_val></_></_>
<_>
<!-- tree 13 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
10 13 4 4 -1.</_>
<_>
12 13 2 2 2.</_>
<_>
10 15 2 2 2.</_></rects>
<tilted>0</tilted></feature>
<threshold>-7.0174131542444229e-03</threshold>
<left_val>-0.4878580868244171</left_val>
<right_val>-4.7722761519253254e-03</right_val></_></_>
<_>
<!-- tree 14 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
4 17 1 3 -1.</_>
<_>
4 18 1 1 3.</_></rects>
<tilted>0</tilted></feature>
<threshold>-5.6818639859557152e-04</threshold>
<left_val>0.3031811118125916</left_val>
<right_val>-0.1906266957521439</right_val></_></_>
<_>
<!-- tree 15 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
12 12 8 3 -1.</_>
<_>
12 12 4 3 2.</_></rects>
<tilted>0</tilted></feature>
<threshold>-0.0346436500549316</threshold>
<left_val>0.1061747968196869</left_val>
<right_val>-0.1113270968198776</right_val></_></_>
<_>
<!-- tree 16 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
5 13 8 4 -1.</_>
<_>
5 13 4 2 2.</_>
<_>
9 15 4 2 2.</_></rects>
<tilted>0</tilted></feature>
<threshold>0.0128513900563121</threshold>
<left_val>0.1139544025063515</left_val>
<right_val>-0.6669226884841919</right_val></_></_>
<_>
<!-- tree 17 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
0 0 20 18 -1.</_>
<_>
0 9 20 9 2.</_></rects>
<tilted>0</tilted></feature>
<threshold>0.2961465120315552</threshold>
<left_val>-0.1820058971643448</left_val>
<right_val>0.3209075033664703</right_val></_></_>
<_>
<!-- tree 18 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
5 17 1 2 -1.</_>
<_>
5 18 1 1 2.</_></rects>
<tilted>0</tilted></feature>
<threshold>-1.3540580403059721e-03</threshold>
<left_val>-0.7073159813880920</left_val>
<right_val>0.0918638333678246</right_val></_></_>
<_>
<!-- tree 19 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
17 18 3 2 -1.</_>
<_>
17 19 3 1 2.</_></rects>
<tilted>0</tilted></feature>
<threshold>-7.0616841549053788e-04</threshold>
<left_val>0.1960162967443466</left_val>
<right_val>-0.1338178962469101</right_val></_></_>
<_>
<!-- tree 20 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
4 8 7 3 -1.</_>
<_>
4 9 7 1 3.</_></rects>
<tilted>0</tilted></feature>
<threshold>-5.4999729618430138e-03</threshold>
<left_val>0.3074981868267059</left_val>
<right_val>-0.1724286973476410</right_val></_></_>
<_>
<!-- tree 21 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
7 9 13 2 -1.</_>
<_>
7 10 13 1 2.</_></rects>
<tilted>0</tilted></feature>
<threshold>-0.0122836297377944</threshold>
<left_val>0.1942628026008606</left_val>
<right_val>-0.1230755969882011</right_val></_></_>
<_>
<!-- tree 22 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
7 12 2 1 -1.</_>
<_>
8 12 1 1 2.</_></rects>
<tilted>0</tilted></feature>
<threshold>1.9181630341336131e-04</threshold>
<left_val>0.1334999054670334</left_val>
<right_val>-0.3691028952598572</right_val></_></_>
<_>
<!-- tree 23 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
7 11 6 5 -1.</_>
<_>
9 11 2 5 3.</_></rects>
<tilted>0</tilted></feature>
<threshold>2.7476788964122534e-03</threshold>
<left_val>-0.1872316002845764</left_val>
<right_val>0.2906386852264404</right_val></_></_>
<_>
<!-- tree 24 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
8 14 3 2 -1.</_>
<_>
9 14 1 2 3.</_></rects>
<tilted>0</tilted></feature>
<threshold>5.3845712682232261e-04</threshold>
<left_val>0.1176405027508736</left_val>
<right_val>-0.5548595190048218</right_val></_></_>
<_>
<!-- tree 25 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
17 18 3 2 -1.</_>
<_>
17 19 3 1 2.</_></rects>
<tilted>0</tilted></feature>
<threshold>-6.2914132140576839e-03</threshold>
<left_val>-0.6762797832489014</left_val>
<right_val>0.0256425291299820</right_val></_></_>
<_>
<!-- tree 26 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
0 18 3 2 -1.</_>
<_>
0 19 3 1 2.</_></rects>
<tilted>0</tilted></feature>
<threshold>-8.0435717245563865e-04</threshold>
<left_val>0.3097242116928101</left_val>
<right_val>-0.2231778949499130</right_val></_></_>
<_>
<!-- tree 27 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
16 18 3 2 -1.</_>
<_>
16 19 3 1 2.</_></rects>
<tilted>0</tilted></feature>
<threshold>0.0178245995193720</threshold>
<left_val>0.0100319497287273</left_val>
<right_val>-1.0000309944152832</right_val></_></_>
<_>
<!-- tree 28 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
1 18 3 2 -1.</_>
<_>
1 19 3 1 2.</_></rects>
<tilted>0</tilted></feature>
<threshold>-4.5915339142084122e-03</threshold>
<left_val>-0.7925583124160767</left_val>
<right_val>0.0804975628852844</right_val></_></_>
<_>
<!-- tree 29 -->
<_>
<!-- root node -->
<feature>
<rects>
<_>
11 15 2 2 -1.</_>
<_>
12 15 1 1 2.</_>
<_>
11 16 1 1 2.</_></rects>
<tilted>0</tilted></feature>
<threshold>-4.2610289528965950e-04</threshold>
<left_val>-0.4836213886737823</left_val>
<right_val>0.0490311309695244</right_val></_></_></trees>
<stage_threshold>-1.0918780565261841</stage_threshold>
<parent>11</parent>
<next>-1</next></_></stages></cars3>
</opencv_storage>All the source codes used in this article can be downloaded through this link. I encourage you to download the source code files in order to avoid any typing mistakes in your workbook.
After downloading the tracker file, save it as tracker.py To import in python as a module. We will import the tracker file later. Download the file tracker.pyusing this link.
Functions Available in our Tracker Class
update→ It inputs bounding box coordinates in an array.- Tracker returns a list containing object id and coordinates in the form of [x,y,w,h,
object_id]. - x,y,w,h is the bounding box coordinates of detected objects and
object_idis the unique id given to the objects?
Libraries and Video Feed
Before Starting, we will import the tracker object and initiate a video feed; it could be a camera feed or a video feed.
import cv2
import numpy as np
from tracker import EuclideanDistTracker
tracker = EuclideanDistTracker()
cap = cv2.VideoCapture('RoadRage.mp4')
ret, frame1 = cap.read()
ret, frame2 = cap.read()
We are using the sample highway video provided by OpenCV as a sample.
cap.read() It returns the frame and a boolean value after reading the feed.
Video Feed-In OpenCV
In this part, we will implement object detection using subsequent frame subtraction in OpenCV and use the detected objects for tracking using the tracker class.
Object detection might catch some noise due to unwanted moving objects like trees, leaves etc. we will filter all unwanted moving objects by defining a minimum threshold area.
while cap.isOpened():
diff = cv2.absdiff(frame1, frame2)
gray = cv2.cvtColor(diff, cv2.COLOR_BGR2GRAY)
blur = cv2.GaussianBlur(gray, (5,5), 0 )
height, width = blur.shape
print(height, width)
dilated = cv2.dilate(threshold, (1,1), iterations=1)
contours, _, = cv2.findContours(dilated, cv2.RETR_TREE, cv2.CHAIN_APPROX_SIMPLE)
detections = []
for contour in contours:
(x,y,w,h) = cv2.boundingRect(contour)
if cv2.contourArea(contour) <300:
continue
detections.append([x,y,w,h])
boxes_ids = tracker.update(detections)
for box_id in boxes_ids:
x,y,w,h,id = box_id
cv2.putText(frame1, str(id),(x,y-15), cv2.FONT_HERSHEY_SIMPLEX, 0.8, (0,0,255), 2)
cv2.rectangle(frame1, (x,y),(x+w, y+h), (0,255,0), 2)
cv2.imshow('frame',frame1)
frame1 = frame2
ret, frame2 = cap.read()
key = cv2.waitKey(30)
if key == ord('q):
break
cv2.destroyAllWindows()
cv2.absdiffThis method is used to find the difference between two subsequent frames and based on the difference, we will catch moving objects.- To find the objects, we will apply contouring on the difference of subsequent frames after scaling them into greyscale.
- We will apply a threshold to counter the noise.
- After contours detections, we will filter out contours smaller than 200 px area. Any contours having 300 or more areas will be considered detected objects.
boxes_idsIt contains the associated object Ids and coordinates of bounding boxes.
Output Frame:

Conclusion
In this article, we discussed Object Detection algorithms and learned the process of Euclidean Tracker. Using all the knowledge, we made a Tracker Class and implemented a Tracker in OpenCV.
We made a vehicle counter system using the Euclidean Tracker and object detection using frame subtraction.
Centroid Tracker is easy to implement but inaccurate compared to modern Tracking algorithms. Euclidean and Centroid Tracker Algorithms will fail if objects travel at different speeds. Hence it doesn’t suit the real-world scenario.
- DEEPSORT is a much more robust and accurate deep learning-based tracking algorithm.
- The centroid Tracking algorithm is a multi-step tracking algorithm based on geometrical calculation.
- Pairs with minimum distance difference will be considered as a single object.
- Centroid Tracking algorithms might not be a good fit for real-world problems.
Thanks for Reading!!
The media shown in this article is not owned by Analytics Vidhya and is used at the Author’s discretion.