This article was published as a part of the Data Science Blogathon.
Source: DDI
Introduction
Autoencoders are an unsupervised model that takes unlabeled data and learns effective coding about the data structure that can be applied to another context. It approximates the function that maps the data from input space to lower dimensional coordinates and further approximates to the same dimension of input space so that there is minimum loss.
Autoencoders can be used for a wide variety of tasks like Anomaly detection, Image Compression, Image Search, Image Denoising, etc. So given its popularity and extensive usage in the Industry, it is imperative to have a crystal clear understanding of this to succeed in a data science interview.
In this article, I have compiled a list of five important questions on Autoencoder that you could use as a guide to get more familiar with the topic and also formulate an effective answer to succeed in your next interview.
Interview Questions on Autoencoders
Question 1: What is Autoencoder?
Answer: Autoencoder is a neural network that aims to learn an identity function to reconstruct the original input while simultaneously compressing the data in the process. The reconstructed image is the approximation to input x.
The concept first emerged in the 1980s, and the seminal research paper later publicized by Hinton and Salakhutdinov in 2006.
Figure 1: Diagram illustrating the autoencoder architecture
Source: Lilian Weng
It consists of two networks:
i) Encoder Network: Encoder Network converts the original high-dimension input data into the latent low-dimensional or compressed representation. Consequently, the input size is larger than the output size. In short, the encoder learns to create a compressed/encoded version of the input data and accomplishes the dimensionality reduction.
ii) Decoder Network: Decoder network restores the data from its latent representation, and the original input data to the encoder is nearly identical to the reconstructed input. In short, the decoder reconstructs the original data from the compressed version.
Figure 2: Diagram illustrating compression and decompression/reconstruction of the original image
Source: programmathically.com
The encoder function g(.) is parameterized by ϕ, and the decoder function f(.) is parameterized by θ. The low-dimensional code learned for input x in the bottleneck layer is z=gϕ(x), and the reconstructed input is x′=fθ(gϕ(x)).
The parameters (θ,ϕ) are jointly learned to output a reconstructed data sample that is identical to the original input, x≈fθ(gϕ(x)). Metrics like cross-entropy and MSE loss can be used to quantify the difference between two vectors.
Internally, the bottleneck consists of a hidden layer describing a code representing the input. The hidden layers usually have fewer nodes than the input and output layers to prohibit the networks from learning the identity function. Having fewer nodes in the hidden layers than the input nodes forces the autoencoder to prioritize the useful features it wants to preserve and ignore the noise.
This architecture is helpful for applications like dimensionality reduction or file compression, where we wish to store a version of our data that is more memory efficient or reconstruct a copy (version) of an input that is less noisy than the original data.
When compared to deterministic methods for data compression, autoencoders are learned, meaning that they depend on the features that are specific/unique to the data that the autoencoder has been trained on.
Note: For dimensionality reduction to be efficacious, the lower dimensional features need to have some relationship with each other. The higher the correlation better will be the reconstruction.
Question 2: What will happen if the hidden layer and input layer both have the same number of nodes?
Answer: When the hidden layer and input layer have the same number of nodes, the encoding will resemble the input, making the autoencoder completely useless.
Question 3: Are Autoencoder and PCA the same, or are there any differences?
Answer: No, autoencoder and PCA are not the same things.
Since PCA hasn’t been covered in detail in this post, let me briefly explain it before we talk about the differences between PCA and Autoencoder.
Principal Component Analysis (PCA) is a method that projects/transform the high dimensional data into lower dimensional space while retaining as much info as possible. The variance of data determines the vectors of projections. By limiting the dimensionality to a certain no. of components that make up for most of the variance of the data set, dimensionality reduction is achieved.
Now when it comes to the comparison between PCA and Autoencoder following are some of the differences:
- Principal Component Analysis (PCA) and Autoencoder (Encoder Network) achieve dimensionality reduction. However, Autoencoders are more adaptable.
- PCA can only model linear functions, while Autoencoders can model complex linear and non-linear functions.
- PCA features are linearly uncorrelated with each other because features are projections on an orthogonal basis. However, auto-encoded features can have correlations because they are trained for approximate reconstruction.
- Compared to autoencoders, PCA is faster and computationally cheaper.
- An autoencoder with a single hidden layer and a linear activation function is similar to PCA.
- Because there are so many parameters, autoencoders are susceptible to overfitting. (But regularisation and cautious design choices can prevent this)
Question 4: When should PCA be used, and when should autoencoder?
Answer: In addition to considering computing resources, the choice of technique depends on the properties of the feature space itself. When the features have a non-linear relationship, the autoencoder can compress the data/information better into lower dimensional latent space using its capability to model complex non-linear functions.
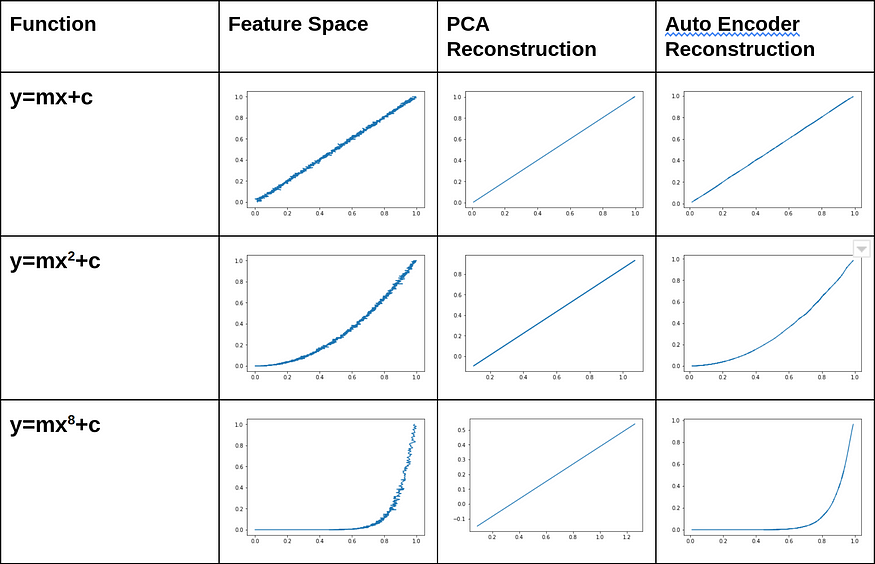
Figure 3: Diagram illustrating the output of PCA and Autoencoder when they are subjected to different 2D functions
Source: Urwa Muaz
Figure 4: Diagram illustrating the output of PCA and Autoencoder when they are subjected to different 3D functions
Source: Urwa Muaz
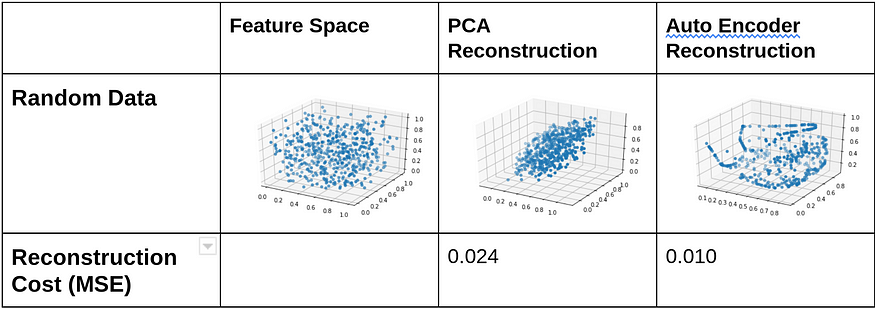
Figure 5: Diagram illustrating the output of PCA and Autoencoder when they are subjected to different random functions
Source: Urwa Muaz
So, from the above diagrams and MSEs, it’s quite evident that whenever there is a non-linear relationship in the feature space, Autoencoder reconstructs more accurately. Contrarily, PCA retains only the projection onto the first principal component, and any other info perpendicular to it is lost.
Question 5: List some applications of Autoencoder.
Answer: Following are some of the applications of Autoencoder:
- Dimensionality Reduction: The encoder network (of the Autoencoder) learns to create a compressed/encoded version of the input data and hence accomplishes the dimensionality reduction
- Feature Extraction: When given unlabeled data, autoencoders can efficiently code out the data’s structure and use that information for supervised learning tasks.
- Image Denoising: The autoencoder receives the noisy input image as input and reconstructs the noiseless output by minimizing the reconstruction loss from the original goal output (noiseless). The trained autoencoder weights can then be used to denoise the original image.
- Image Compression: Autoencoder aims to learn an identity function to reconstruct the original input while at the same time compressing the data in the process. The reconstructed image is the approximation to input x.
- Image Search: The image database can be compressed using autoencoders. The compressed embedding can be used to compare or search using an encoded version of the search image.
- Anomaly Detection: An anomaly detection model can detect a fraudulent transaction or any imbalanced supervised task.
- Missing Value Imputation: The missing values in the dataset can be imputed using denoising autoencoders.
Conclusion
This article presents the five most imperative interview questions on Autoencoders that could be asked in data science interviews. Using these interview questions, you can work on your understanding of different concepts, formulate effective responses, and present them to the interviewer.
To sum it up, the key takeaways from this article are:
1. Autoencoder aims to learn an identity function to reconstruct the original input while at the same time compressing the data in the process. The reconstructed image is the approximation to input x.
2. Autoencoder consists of Encoder and Decoder network.
3. Internally, the bottleneck consists of a hidden layer describing a code representing the input. The hidden layers usually have fewer nodes than the input and output layers to prohibit the networks from learning the identity function.
4. When the hidden layer and input layer have the same number of nodes, the autoencoder will be useless.
5. PCA and Autoencoder (Encoder Network) both achieve dimensionality reduction. However, Autoencoders are more flexible. PCA can only model linear functions, while Autoencoders can model complex linear and non-linear functions.
6. Autoencoders can be used for dimensionality reduction, image search, image compression, missing value imputation, etc.
The media shown in this article is not owned by Analytics Vidhya and is used at the Author’s discretion.
I'm a Researcher who works primarily on various Acoustic DL, NLP, and RL tasks. Here, my writing predominantly revolves around topics related to Acoustic DL, NLP, and RL, as well as new emerging technologies. In addition to all of this, I also contribute to open-source projects @Hugging Face.
For work-related queries please contact: [email protected]
