How to Calculate Cosine Similarity in Python?

Introduction

This article will discuss cosine similarity, a tool for comparing two non-zero vectors. Its effectiveness at determining the orientation of vectors, regardless of their size, leads to its extensive use in domains such as text analysis, data mining, and information retrieval. This article explores the mathematics of cosine similarity and shows how to use it in Python.

Overview: 

• Learn how cosine similarity measures the angle between two vectors to compare their orientation effectively.
• Discover the applications of cosine similarity in text analysis, data mining, and recommendation systems.
• Understand the mathematical foundation of cosine similarity and its practical implementation using Python.
• Gain insights into implementing cosine similarity with NumPy and scikit-learn libraries in Python.
• Explore how cosine similarity is used in real-world scenarios, including document comparison and recommendation systems.

What is Cosine Similarity?

Cosine similarity measures the cosine of the angle between two vectors in a multi-dimensional space. The cosine of two non-zero vectors can be derived by using the Euclidean dot product formula:

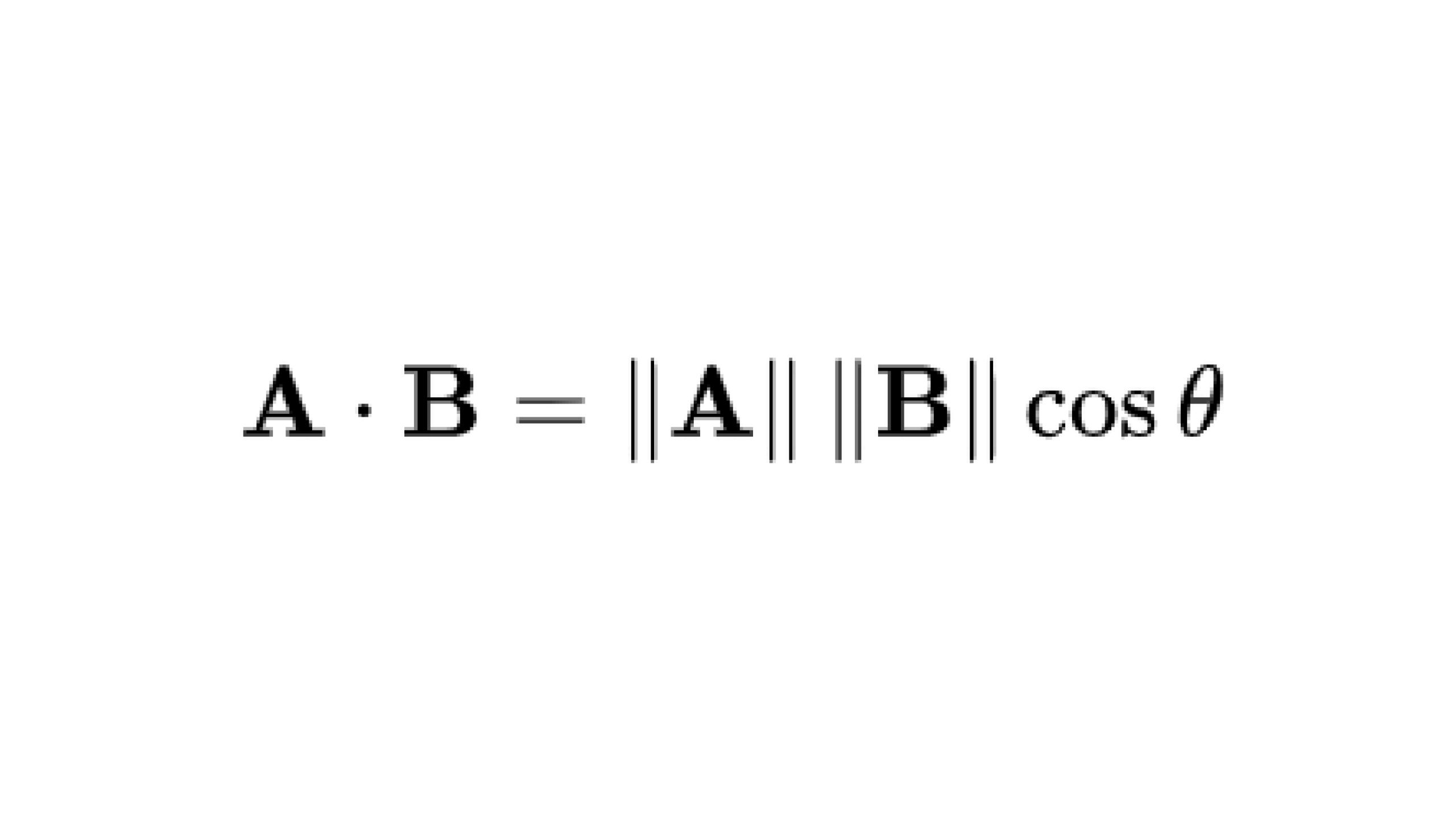
Given two n-dimensional vectors of attributes, A and B, the cosine similarity, cos(θ), is represented using a dot product and magnitude as

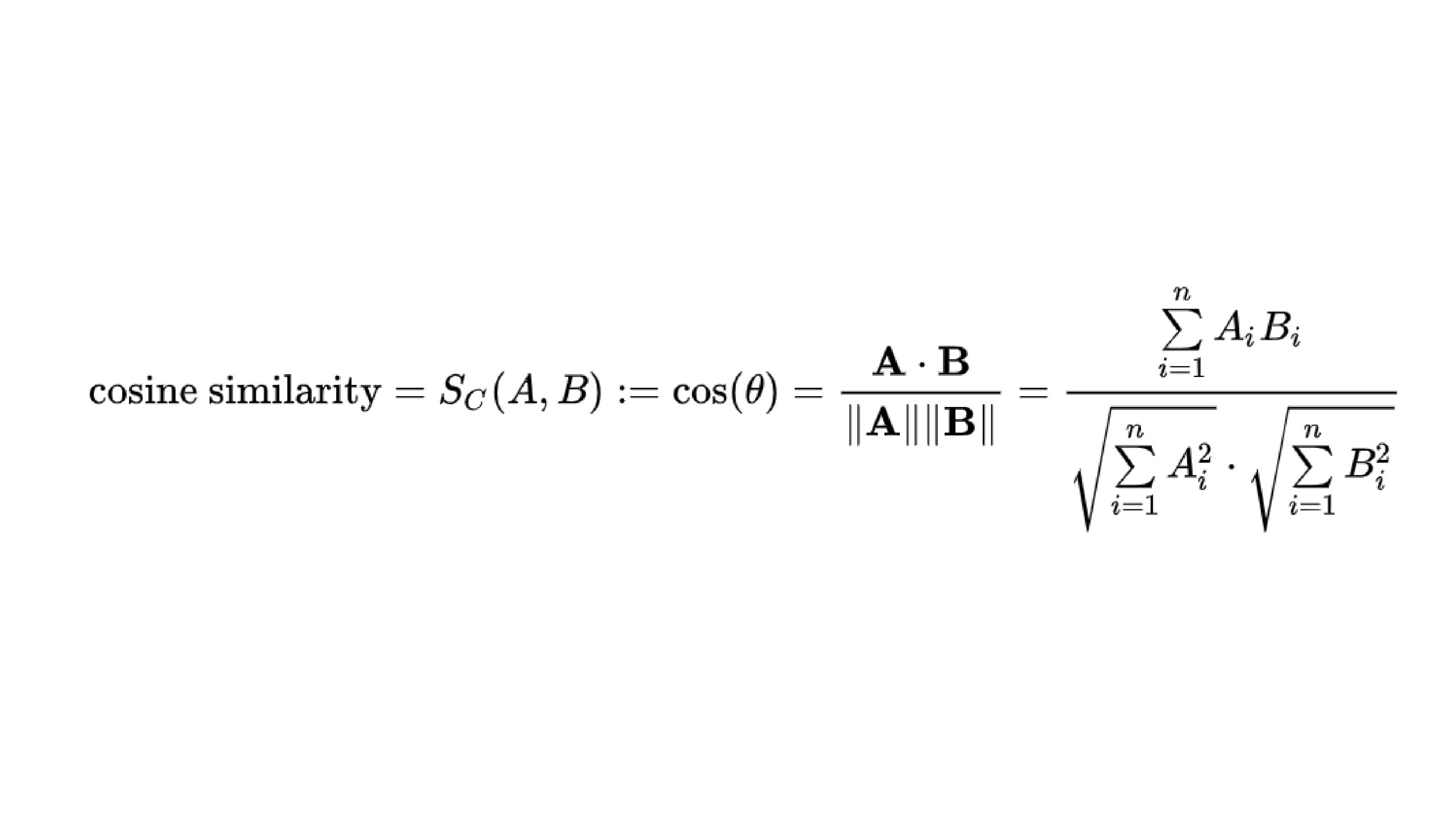
The cosine similarity ranges from -1 to 1, where:

• 1 indicates that the vectors are identical,
• 0 indicates that the vectors are orthogonal (no similarity),
• -1 indicates that the vectors are diametrically opposed.

Applications in Data Science

• Text similarity: In NLP, we use cosine similarity to understand document similarities. We transform texts in those documents into TF-IDF vectors and then use cosine similarity to find their similarities.
• Recommendation Systems: Let’s say we have a music recommendation system. Here, we calculate the similarity between users, and based on the score, we suggest songs or music to other users. Generally, recommendation systems use cosine similarity in collaborative filtering or other filtering techniques to suggest items for our users.

Implementation of Cosine Similarity

Let us now learn how to implement cosine similarity using different libraries:

Implementation Using Numpy Library

# Using numpy
import numpy as np

# Define two vectors
A = np.array([1, 2, 3])
B = np.array([4, 5, 6])

# Compute cosine similarity
cos_sim = np.dot(A, B) / (np.linalg.norm(A) * np.linalg.norm(B))
print("Cosine Similarity (NumPy):", cos_sim)

Here, we are creating two arrays, A and B, which will act as the vectors we need to compare. We use the cosine similarity formula, i.e., the dot product of A and B upon mod of A X mod B.

Implementation Using Scikit-learn Library

from sklearn.metrics.pairwise import cosine_similarity

# Define two vectors
A = [[1, 2, 3]]
B = [[4, 5, 6]]

# Compute cosine similarity
cos_sim = cosine_similarity(A, B)
print("Cosine Similarity (scikit-learn):", cos_sim[0][0])

Here, we can see that the inbuilt function in the sklearn library does our job of finding the cosine similarity.

Step-By-Step Mathematics Behind the Numpy Code

Conclusion

Cosine similarity is a powerful tool for finding the similarity between vectors, particularly useful in high-dimensional and sparse datasets. In this article, we have also seen the implementation of cosine similarity using Python, which is very straightforward. We have used Python’s NumPy and scikit-learn libraries to implement cosine similarity. Cosine similarity is important in NLP, text analysis, and recommendation systems because it is independent of the magnitude of the vector.

Frequently Asked Questions

Badrinarayan M

Data science Trainee at Analytics Vidhya, specializing in ML, DL and Gen AI. Dedicated to sharing insights through articles on these subjects. Eager to learn and contribute to the field's advancements. Passionate about leveraging data to solve complex problems and drive innovation.