What is Adaptive Gradient(Adagrad) Optimizer?

Imagine you’re planting a garden with a variety of plants, each requiring a different amount of water. If you used the same amount of water on all of them every day, some plants would thrive, while others might get overwatered or dry out. In machine learning, a similar challenge exists with gradient descent, where using the same learning rate for all parameters can slow down learning or lead to poor performance. This is where Adagrad comes in. It adjusts the step size for each parameter based on how much it has changed during training, helping the model adapt to the unique “needs” of each feature, especially when they vary in scale.

What is Adagrad(Adaptive Gradient)?

Adagrad (Adaptive Gradient) is an optimization algorithm widely used in machine learning, particularly for training deep neural networks. It dynamically adjusts the learning rate for each parameter based on its past gradients. This adaptability enhances training efficiency, especially in scenarios involving sparse data or parameters that converge at different rates.

By assigning higher learning rates to less frequent features and lower rates to more common ones, Adagrad excels in handling sparse data. Moreover, it eliminates the need for manual learning rate adjustments, simplifying the training process.

Working of Adagrad Algorithm?

Step 1: Initialize Parameters

The first step in Adagrad is to initialize the necessary components before starting the optimization process. The parameters being optimized, such as weights in a neural network, are given initial values, often random or zero, depending on the application. Alongside the parameters, a small constant epsilon ϵ is set, to avoid division by zero errors in later computations. Finally, the initial learning rate is chosen to control how large the parameter updates are at each step. The learning rate is typically selected based on experimentation or prior knowledge about the problem. These initial settings are crucial because they influence the behaviour of the optimizer and its ability to converge to a solution.

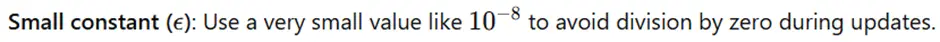
Step 2: Compute the Gradient

At each time step t, the gradient of the loss function with respect to each parameter is calculated. This gradient indicates the direction and magnitude of the changes needed to reduce the loss. The gradient provides the “slope” of the loss function, showing how the parameters should be adjusted to minimize the error. This computation is repeated for all parameters and is critical because it guides the optimizer in updating the parameters effectively. The accuracy and stability of these gradients depend on the properties of the loss function and the data being used.

g_t​ = ∇f(θ_t​)

• f(θ_t​): Loss Function
• g_t​: current gradient

Step 3: Accumulate the Squared Gradients

Instead of applying the gradient directly to update the parameters, Adagrad introduces an accumulation step where the squared gradients are summed over time. For each parameter ‘i’, this accumulated squared gradient​ is computed as:

G_t​=G_t−1​+g_t²

• G_t−1​: Accumulated squared gradients from previous steps.
• g_t^2​: Square of the current gradient (element-wise if vectorized).

This step ensures that the optimizer keeps track of how much each parameter has been updated historically. Parameters with large accumulated gradients are effectively “penalized” in subsequent updates, while those with smaller accumulated gradients retain higher learning rates. This mechanism allows Adagrad to dynamically adjust the learning rate for each parameter, making it particularly useful in cases where gradients differ significantly across parameters, such as in sparse data scenarios.

Step 4: Update the Parameters

Once the accumulated gradient is computed, the parameters are updated using Adagrad’s update rule:

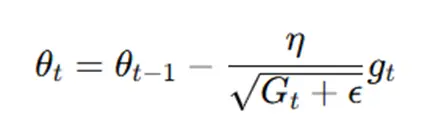
The denominator adjusts the learning rate for each parameter based on its accumulated gradient history. Parameters with large accumulated gradients have smaller updates due to the larger denominator, which prevents overshooting and promotes stability. Conversely, parameters with small accumulated gradients have larger updates, ensuring they are not neglected during training. This adaptive adjustment of learning rates enables Adagrad to handle varying parameter sensitivities effectively.

Also read: Gradient Descent Algorithm: How Does it Work in Machine Learning?

How Adagrad Adapts the Learning Rate?

Parameters with frequent updates :

Large accumulated gradients cause the term to shrink.

This reduces the learning rate for these parameters, slowing down their updates to prevent instability.

Parameters with infrequent updates:

Small accumulated gradients keep larger.

This ensures larger updates for these parameters, enabling effective learning.

Why Adagrad’s Adjustment Matters?

Adagrad’s dynamic learning rate adjustment makes it particularly well-suited for problems where some parameters require frequent updates while others are updated less often. For example, in natural language processing, words that appear frequently in the data will have large accumulated gradients, reducing their learning rates and stabilizing their updates. In contrast, rare words will retain higher learning rates, ensuring they receive adequate updates. However, the accumulation of squared gradients can cause the learning rates to decay too much over time, slowing convergence in long training sessions. Despite this drawback, Adagrad is a powerful and intuitive optimization algorithm for scenarios where per-parameter learning rate adaptation is beneficial.

Also read: Complete Guide to Gradient-Based Optimizers in Deep Learning

Implementation for Better Understanding

1. Importing Necessary Libraries

import numpy as np
from sklearn.datasets import fetch_california_housing
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler

2. Define the Gradient Descent Linear Regression Class

class GradientDescentLinearRegression:
    def __init__(self, learning_rate=1, max_iterations=10000, eps=1e-6):
        # Initialize hyperparameters
        self.learning_rate = learning_rate
        self.max_iterations = max_iterations
        self.eps = eps

The __init__ method initializes the class by setting key hyperparameters for gradient descent optimization: learning_rate, which controls the step size for weight updates; max_iterations, the maximum number of iterations to prevent infinite loops; and eps, a small threshold for stopping the optimization when weight changes are negligible, signaling convergence. These parameters ensure the training process is both efficient and precise, with flexibility for customization based on the dataset and requirements. For instance, users can modify these values to balance speed and accuracy or rely on the default settings for general purposes.

3. Define the Predict Method

def predict(self, X):
        return np.dot(X, self.w.T)
    

This method calculates predictions by computing the dot product of the input features (X) and the weight vector (w). It represents the core functionality of linear regression, where the predicted values are a linear combination of the input features.

4. Define the Cost Methods

def cost(self, X, y):
        y_pred = self.predict(X)
        loss = (y - y_pred) ** 2
        return np.mean(loss)

The cost method calculates the Mean Squared Error (MSE) loss, which measures the difference between actual target values (y) and predicted values (y_pred). This function guides the optimization process by quantifying the model’s performance.

5. Define the Grad Method

def grad(self, X, y):
        y_pred = self.predict(X)
        d_intercept = -2 * sum(y - y_pred)                  
        d_x = -2 * sum(X[:, 1:] * (y - y_pred).reshape(-1, 1))  
        g = np.append(np.array(d_intercept), d_x)          
        return g / X.shape[0]

This method computes the gradient of the cost function concerning the model’s weights. The gradient indicates the direction in which the weights should be adjusted to minimize the cost. It separately computes the gradients for the intercept and feature weights.

6. Define the Adagrad Method

def adagrad(self, g):
        self.G += g**2  
        step = self.learning_rate / (np.sqrt(self.G + self.eps)) * g
        return step

The Adagrad method implements the AdaGrad optimization technique, which adjusts the learning rate for each weight dynamically based on the accumulated gradient squared (G). This approach is particularly effective for sparse data or when dealing with weights updated at varying rates.

7. Define the Fit Method

def fit(self, X, y, method="adagrad", verbose=True):
        # Initialize weights and AdaGrad cache if needed
        self.w = np.zeros(X.shape[1])  # Initialize weights
        if method == "adagrad":
            self.G = np.zeros(X.shape[1])  # Initialize AdaGrad cache
        w_hist = [self.w]  # History of weights
        cost_hist = [self.cost(X, y)]  # History of cost function values
        for iter in range(self.max_iterations):
            g = self.grad(X, y)  # Compute the gradient
            if method == "standard":
                step = self.learning_rate * g  # Standard gradient descent step
            elif method == "adagrad":
                step = self.adagrad(g)  # AdaGrad step
            else:
                raise ValueError("Method not supported.")
            self.w = self.w - step  # Update weights
            w_hist.append(self.w)  # Save weight history
            J = self.cost(X, y)  # Compute cost
            cost_hist.append(J)  # Save cost history
            if verbose:
                print(f"Iter: {iter}, Gradient: {g}, Weights: {self.w}, Cost: {J}")
            # Stop if weight updates are smaller than the threshold
            if np.linalg.norm(w_hist[-1] - w_hist[-2]) < self.eps:
                break
        # Store history and optimization method used
        self.iterations = iter + 1
        self.w_hist = w_hist
        self.cost_hist = cost_hist
        self.method = method
        return self   

The fit method trains the linear regression model using gradient descent. It initializes the weight vector (w) and accumulates gradient information if using AdaGrad. In each iteration, it computes the gradient, updates the weights, and calculates the current cost. If the weight changes become too small (less than eps), the training halts early. Verbose output optionally provides detailed logs of the optimization process.

Here’s the full code:

# Import necessary libraries
import numpy as np
from sklearn.datasets import fetch_california_housing
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
# Define the custom Gradient Descent Linear Regression class
class GradientDescentLinearRegression:
    def __init__(self, learning_rate=1, max_iterations=10000, eps=1e-6):
        # Initialize hyperparameters
        self.learning_rate = learning_rate
        self.max_iterations = max_iterations
        self.eps = eps
    def predict(self, X):
        return np.dot(X, self.w.T)  # Linear regression prediction: X*w^T
    def cost(self, X, y):
        y_pred = self.predict(X)
        loss = (y - y_pred) ** 2
        return np.mean(loss)
    def grad(self, X, y):
        y_pred = self.predict(X)
        d_intercept = -2 * sum(y - y_pred)                  
        d_x = -2 * sum(X[:, 1:] * (y - y_pred).reshape(-1, 1))  
        g = np.append(np.array(d_intercept), d_x)          
        return g / X.shape[0]                              
    def adagrad(self, g):
        self.G += g**2  
        step = self.learning_rate / (np.sqrt(self.G + self.eps)) * g
        return step
    def fit(self, X, y, method="adagrad", verbose=True):
        # Initialize weights and AdaGrad cache if needed
        self.w = np.zeros(X.shape[1])  # Initialize weights
        if method == "adagrad":
            self.G = np.zeros(X.shape[1])  # Initialize AdaGrad cache
        w_hist = [self.w]  # History of weights
        cost_hist = [self.cost(X, y)]  # History of cost function values
        for iter in range(self.max_iterations):
            g = self.grad(X, y)  # Compute the gradient
            if method == "standard":
                step = self.learning_rate * g  # Standard gradient descent step
            elif method == "adagrad":
                step = self.adagrad(g)  # AdaGrad step
            else:
                raise ValueError("Method not supported.")
            self.w = self.w - step  # Update weights
            w_hist.append(self.w)  # Save weight history
            J = self.cost(X, y)  # Compute cost
            cost_hist.append(J)  # Save cost history
            if verbose:
                print(f"Iter: {iter}, Gradient: {g}, Weights: {self.w}, Cost: {J}")
            # Stop if weight updates are smaller than the threshold
            if np.linalg.norm(w_hist[-1] - w_hist[-2]) < self.eps:
                break
        # Store history and optimization method used
        self.iterations = iter + 1
        self.w_hist = w_hist
        self.cost_hist = cost_hist
        self.method = method
        return self
# Load the California housing dataset
data = fetch_california_housing()
X, y = data.data, data.target
# Split the dataset into training and testing sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# Standardize the feature data
scaler = StandardScaler()
X_train = scaler.fit_transform(X_train)
X_test = scaler.transform(X_test)
# Train and evaluate the model using standard gradient descent
model = GradientDescentLinearRegression(learning_rate=0.1, max_iterations=1000, eps=1e-6)
model.fit(X_train, y_train, method="standard", verbose=False)
y_pred = model.predict(X_test)  # Predict test data
mse = np.mean((y_test - y_pred) ** 2)  # Compute MSE
print("Final Weights (Standard):", model.w)
print("Mean Squared Error (Standard GD):", mse)
# Train and evaluate the model using AdaGrad
model = GradientDescentLinearRegression(learning_rate=0.1, max_iterations=1000, eps=1e-6)
model.fit(X_train, y_train, method="adagrad", verbose=False)
y_pred = model.predict(X_test)  # Predict test data
mse = np.mean((y_test - y_pred) ** 2)  # Compute MSE
print("Final Weights (AdaGrad):", model.w)
print("Mean Squared Error (AdaGrad):", mse)

Also read: A Comprehensive Guide on Optimizers in Deep Learning

Applications of Adagrad Optimizer

Here are the applications of Adagrad Optimizer:

1. Natural Language Processing (NLP): Adagrad is extensively used for tasks like sentiment analysis, text classification, language modeling, and machine translation. Its adaptive learning rates are particularly effective in optimizing sparse embeddings, which are common in NLP tasks​.
2. Recommender Systems: The optimizer is applied to personalize recommendations by dynamically adjusting learning rates. This capability helps models handle sparse datasets, which are typical in recommendation scenarios​.
3. Time Series Analysis: It is used for forecasting tasks like stock price predictions, where data patterns can be non-uniform and need adaptive learning rate adjustments​.
4. Image Recognition: While not as common as other optimizers like Adam, Adagrad has been used in computer vision tasks for efficiently training models where certain features require higher learning rates​.
5. Speech and Audio Processing: Similar to NLP, Adagrad can optimize models for tasks like speech recognition and audio classification, especially when handling sparse feature representations​

Limitations of Adagrad

Here are the limitations of Adagrad:

1. Aggressive Learning Rate Decay: Adagrad accumulates the squared gradients over all iterations. This accumulation grows continuously, leading to a drastic reduction in the learning rate.This aggressive decay can cause the algorithm to stop learning prematurely, especially in later stages of training.
2. Poor Performance on Non-Convex Problems: For complex non-convex optimization problems, Adagrad’s decreasing learning rate can hinder its ability to escape from saddle points or local minima, slowing convergence.
3. Computational Overhead: Adagrad requires maintaining a per-parameter learning rate and accumulative squared gradients. This can lead to increased memory consumption and computational overhead, especially for large-scale models.

Conclusion

AdaGrad is one of the variants of optimization algorithms that have made massive contributions toward advancing the development of machine learning. It creates adaptive learning rates specific to the needs of every sparse data-compatible parameter, adjusts step sizes, dynamically changes, and learns from it, which explains why it turns out to be useful in domains like natural language processing, recommender systems, and time-series analysis.

However, all of these strengths came at a great cost: sharp learning rate decay, poor optimization on nonconvex problems, and high computational overhead. This produced successors: AdaDelta and RMSProp, which avoided the weaknesses of AdaGrad while keeping at least some of the main strengths.

Despite all these limitations, AdaGrad intuitively and effectively is a good choice for problems that either have sparse data or features with varying sensitivities; hence it is a cornerstone in the evolution of adaptive optimization techniques. Its simplicity and effectiveness continued to make it foundational for learners and practitioners in the field of machine learning.

If you are looking for an AI/ML course online, then explore: Certified AI & ML BlackBelt PlusProgram

Frequently Asked Questions