Neural Network Weight Quantization

In the age of increasingly large language models and complex neural networks, optimizing model efficiency has become paramount. Weight quantization stands out as a crucial technique for reducing model size and improving inference speed without significant performance degradation. This guide provides a hands-on approach to implementing and understanding weight quantization, using GPT-2 as our practical example.

Learning Objectives

• Understand the fundamentals of weight quantization and its importance in model optimization.
• Learn the differences between absmax and zero-point quantization techniques.
• Implement weight quantization methods on GPT-2 using PyTorch.
• Analyze the impact of quantization on memory efficiency, inference speed, and accuracy.
• Visualize quantized weight distributions using histograms for insights.
• Evaluate model performance post-quantization through text generation and perplexity metrics.
• Explore the advantages of quantization for deploying models on resource-constrained devices.

This article was published as a part of the Data Science Blogathon.

Understanding Weight Quantization Fundamentals

Weight quantization converts high-precision floating-point weights (typically 32-bit) to lower-precision representations (commonly 8-bit integers). This process significantly reduces model size and memory usage while attempting to preserve model performance. The key challenge lies in maintaining model accuracy while reducing numerical precision.

Why Quantize?

• Memory Efficiency: Reducing precision from 32-bit to 8-bit can theoretically reduce model size by 75%
• Faster Inference: Integer operations are generally faster than floating-point operations
• Lower Power Consumption: Reduced memory bandwidth and simpler computations lead to energy savings
• Deployment Flexibility: Smaller models can be deployed on resource-constrained devices

Practical Implementation

Let’s dive into implementing two popular quantization methods: absmax quantization and zero-point quantization.

Setting Up the Environment

First, we’ll set up our development environment with necessary dependencies:

import seaborn as sns
import torch
import numpy as np
from transformers import AutoModelForCausalLM, AutoTokenizer
from copy import deepcopy
import matplotlib.pyplot as plt
import matplotlib.ticker as ticker
import seaborn as sns

Below we will look into implementing quantization methods:

Absmax Quantization

The absmax quantization method scales weights based on the maximum absolute value in the tensor:

# Define quantization functions
def absmax_quantize(X):
    scale = 100 / torch.max(torch.abs(X))  # Adjusted scale
    X_quant = (scale * X).round()
    X_dequant = X_quant / scale
    return X_quant.to(torch.int8), X_dequant

This method works by:

• Finding the maximum absolute value in the weight tensor
• Computing a scaling factor to fit values within int8 range
• Scaling and rounding the values
• Providing both quantized and dequantized versions

Key advantages:

• Simple implementation
• Good preservation of large values
• Symmetric quantization around zero

Zero-point Quantization

Zero-point quantization adds an offset to better handle asymmetric distributions:

def zeropoint_quantize(X):
    x_range = torch.max(X) - torch.min(X)
    x_range = 1 if x_range == 0 else x_range
    scale = 200 / x_range
    zeropoint = (-scale * torch.min(X) - 128).round()
    X_quant = torch.clip((X * scale + zeropoint).round(), -128, 127)
    X_dequant = (X_quant - zeropoint) / scale
    return X_quant.to(torch.int8), X_dequant

Output:

Using device: cuda

This method:

• Calculates the full range of values
• Determines scale and zero-point parameters
• Applies scaling and shifting
• Clips values to ensure int8 bounds

Benefits:

• Better handling of asymmetric distributions
• Improved representation of near-zero values
• Often results in better overall accuracy

Loading and Preparing the Model

Let’s apply these quantization methods to a real model. We’ll use GPT-2 as our example:

# Load model and tokenizer
model_id = 'gpt2'
model = AutoModelForCausalLM.from_pretrained(model_id).to(device)
tokenizer = AutoTokenizer.from_pretrained(model_id)

# Print model size
print(f"Model size: {model.get_memory_footprint():,} bytes")

Output:

Quantization Process: Weights and Model

Dive into applying quantization techniques to both individual weights and the entire model. This step ensures reduced memory usage and computational efficiency while maintaining performance.

# Quantize and visualize weights
weights_abs_quant, _ = absmax_quantize(weights)
weights_zp_quant, _ = zeropoint_quantize(weights)


# Quantize the entire model
model_abs = deepcopy(model)
model_zp = deepcopy(model)

for param in model_abs.parameters():
    _, dequantized = absmax_quantize(param.data)
    param.data = dequantized

for param in model_zp.parameters():
    _, dequantized = zeropoint_quantize(param.data)
    param.data = dequantized

Visualizing Quantized Weight Distributions

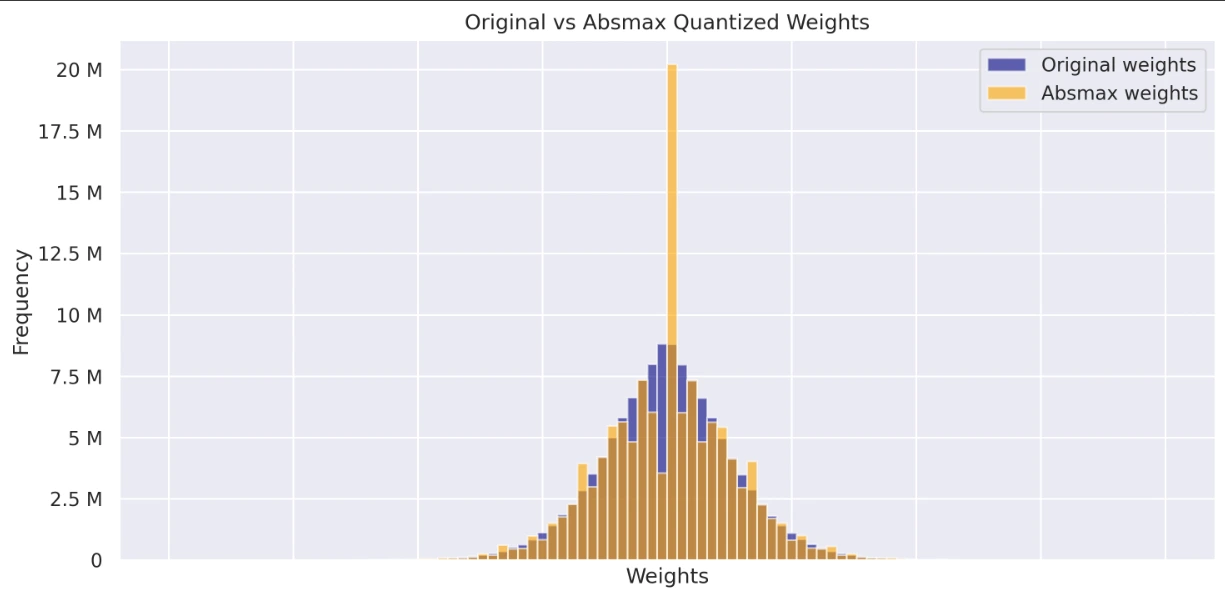
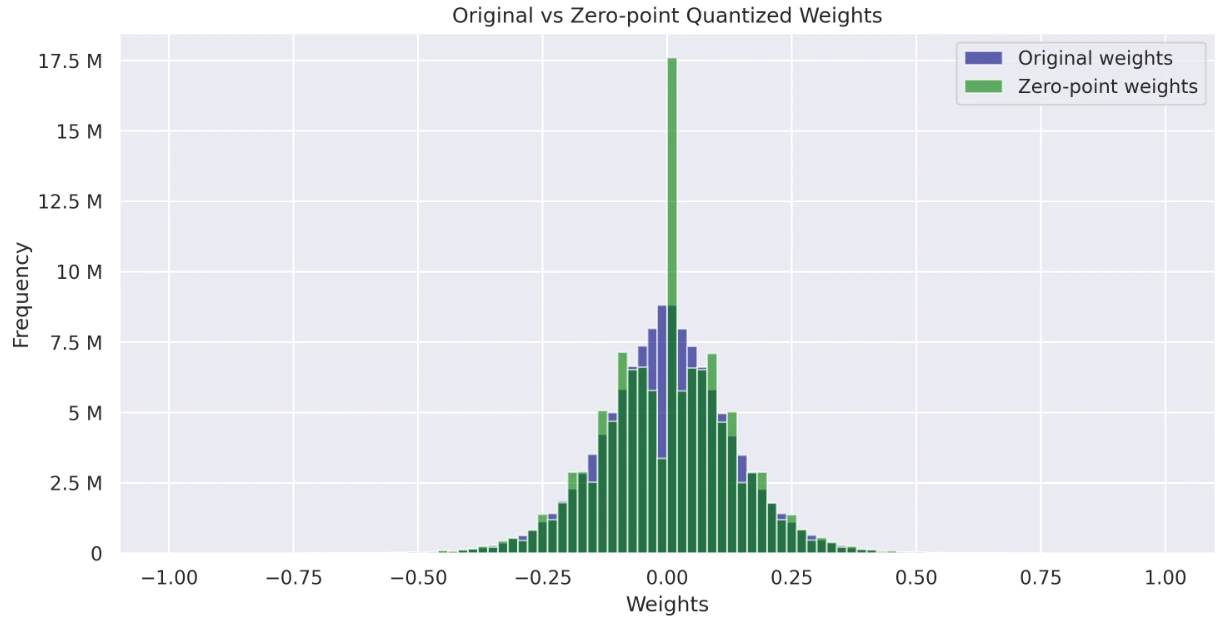
Visualize and compare the weight distributions of the original, absmax quantized, and zero-point quantized models. These histograms provide insights into how quantization impacts weight values and their overall distribution.

# Visualize histograms of weights
def visualize_histograms(original_weights, absmax_weights, zp_weights):
    sns.set_theme(style="darkgrid")
    fig, axs = plt.subplots(2, figsize=(10, 10), dpi=300, sharex=True)

    axs[0].hist(original_weights, bins=100, alpha=0.6, label='Original weights', color='navy', range=(-1, 1))
    axs[0].hist(absmax_weights, bins=100, alpha=0.6, label='Absmax weights', color='orange', range=(-1, 1))

    axs[1].hist(original_weights, bins=100, alpha=0.6, label='Original weights', color='navy', range=(-1, 1))
    axs[1].hist(zp_weights, bins=100, alpha=0.6, label='Zero-point weights', color='green', range=(-1, 1))

    for ax in axs:
        ax.legend()
        ax.set_xlabel('Weights')
        ax.set_ylabel('Frequency')
        ax.yaxis.set_major_formatter(ticker.EngFormatter())

    axs[0].set_title('Original vs Absmax Quantized Weights')
    axs[1].set_title('Original vs Zero-point Quantized Weights')
    plt.tight_layout()
    plt.show()

# Flatten weights for visualization
original_weights = np.concatenate([param.data.cpu().numpy().flatten() for param in model.parameters()])
absmax_weights = np.concatenate([param.data.cpu().numpy().flatten() for param in model_abs.parameters()])
zp_weights = np.concatenate([param.data.cpu().numpy().flatten() for param in model_zp.parameters()])

visualize_histograms(original_weights, absmax_weights, zp_weights)

The code includes a comprehensive visualization function:

• Graph displaying Original Weights vs Absmax Weights
• Graph displaying Original Weights vs Zero-point Weights

Output:

Performance Evaluation

Evaluating the impact of quantization on model performance is essential to ensure efficiency and accuracy. Let’s measure how well the quantized models perform compared to the original.

Text Generation

Explore how the quantized models generate text and compare the quality of outputs to the original model’s predictions.

def generate_text(model, input_text, max_length=50):
    input_ids = tokenizer.encode(input_text, return_tensors='pt').to(device)
    output = model.generate(inputs=input_ids,
                            max_length=max_length,
                            do_sample=True,
                            top_k=30,
                            pad_token_id=tokenizer.eos_token_id,
                            attention_mask=input_ids.new_ones(input_ids.shape))
    return tokenizer.decode(output[0], skip_special_tokens=True)

# Generate text with original and quantized models
original_text = generate_text(model, "The future of AI is")
absmax_text   = generate_text(model_abs, "The future of AI is")
zp_text       = generate_text(model_zp, "The future of AI is")



print(f"Original model:\n{original_text}")
print("-" * 50)
print(f"Absmax model:\n{absmax_text}")
print("-" * 50)
print(f"Zeropoint model:\n{zp_text}")

This code compares text generation outputs from three models: the original, an “absmax” quantized model, and a “zeropoint” quantized model. It uses a generate_text function to generate text based on an input prompt, applying sampling with a top-k value of 30. Finally, it prints the results from all three models.

Output:

# Perplexity evaluation
def calculate_perplexity(model, text):
    encodings = tokenizer(text, return_tensors='pt').to(device)
    input_ids = encodings.input_ids
    with torch.no_grad():
        outputs = model(input_ids, labels=input_ids)
    return torch.exp(outputs.loss)

long_text = "Artificial intelligence is a transformative technology that is reshaping industries."

ppl_original = calculate_perplexity(model, long_text)
ppl_absmax = calculate_perplexity(model_abs, long_text)
ppl_zp = calculate_perplexity(model_zp, long_text)

print(f"\nPerplexity (Original): {ppl_original.item():.2f}")
print(f"Perplexity (Absmax): {ppl_absmax.item():.2f}")
print(f"Perplexity (Zero-point): {ppl_zp.item():.2f}")

The code calculates the perplexity (a measure of how well a model predicts text) for a given input using three models: the original, “absmax” quantized, and “zeropoint” quantized models. Lower perplexity indicates better performance. It prints the perplexity scores for comparison.

Output:

You can access colab link here.

Advantages of Weight Quantization

Below we will look into the advantages of weight quantization:

• Memory Efficiency: Quantization reduces model size by up to 75%, enabling faster loading and inference.
• Faster Inference: Integer operations are faster than floating-point operations, leading to quicker model execution.
• Lower Power Consumption: Reduced memory bandwidth and simplified computation lead to energy savings, essential for edge devices and mobile deployment.
• Deployment Flexibility: Smaller models are easier to deploy on hardware with limited resources (e.g., mobile phones, embedded devices).
• Minimal Performance Degradation: With the right quantization strategy, models can retain most of their accuracy despite the reduced precision.

Conclusion

Weight quantization plays a crucial role in enhancing the efficiency of large language models, particularly when it comes to deploying them on resource-constrained devices. By converting high-precision weights to lower-precision integer representations, we can significantly reduce memory usage, improve inference speed, and lower power consumption, all without severely affecting the model’s performance.

In this guide, we explored two popular quantization techniques—absmax quantization and zero-point quantization—using GPT-2 as a practical example. Both techniques demonstrated the ability to reduce the model’s memory footprint and computational requirements while maintaining a high level of accuracy in text generation tasks. However, the zero-point quantization method, with its asymmetric approach, generally resulted in better preservation of model accuracy, especially for non-symmetric weight distributions.

Key Takeaways

• Absmax Quantization is simpler and works well for symmetric weight distributions, though it might not capture asymmetric distributions as effectively as zero-point quantization.
• Zero-point Quantization offers a more flexible approach by introducing an offset to handle asymmetric distributions, often leading to better accuracy and a more efficient representation of weights.
• Quantization is essential for deploying large models in real-time applications where computational resources are limited.
• Despite the quantization process reducing precision, it’s possible to maintain model performance close to the original with proper tuning and quantization strategies.
• Visualization techniques like histograms can provide insights into how quantization affects model weights and the distribution of values in the tensors.

Frequently Asked Questions

The media shown in this article is not owned by Analytics Vidhya and is used at the Author’s discretion.

Nilesh Dwivedi

My name is Nilesh Dwivedi, and I'm excited to join this vibrant community of bloggers and readers. I'm currently in my first year of BTech, specializing in Data Science and Artificial Intelligence at IIIT Dharwad. I'm passionate about technology and data science and looking forward to write more blogs.