Evaluating language models has always been a challenging task. How do we measure if a model truly understands language, generates coherent text, or produces accurate responses? Among the various metrics developed for this purpose, the Perplexity Metric stands out as one of the most fundamental and widely used evaluation metrics in the field of Natural Language Processing (NLP) and Language Model (LM) assessment.
Perplexity has been used since the early days of statistical language modeling and continues to be relevant even in the era of large language models (LLMs). In this article, we’ll dive deep into perplexity—what it is, how it works, its mathematical foundations, implementation details, advantages, limitations, and how it compares to other evaluation metrics.
By the end of this article, you’ll have a thorough understanding of perplexity and be able to implement it yourself to evaluate language models.
Table of contents
- What is Perplexity Metric?
- How Does Perplexity Work?
- How is Perplexity Calculated?
- Alternate Representations of Perplexity Metric
- Implementation of Perplexity Metric from Scratch in Python
- Example and Output
- Implementing Perplexity Metric in NLTK
- Advantages of Perplexity
- Limitations of Perplexity
- Overcoming Limitations Using LLM-as-a-Judge
- Practical Applications
- Comparison with Other LLM Evaluation Metrics
- Conclusion
What is Perplexity Metric?
Perplexity Metric is a measurement of how well a probability model predicts a sample. In the context of language models, perplexity quantifies how “surprised” or “confused” a model is when encountering a text sequence. The lower the perplexity, the better the model is at predicting the sample text.
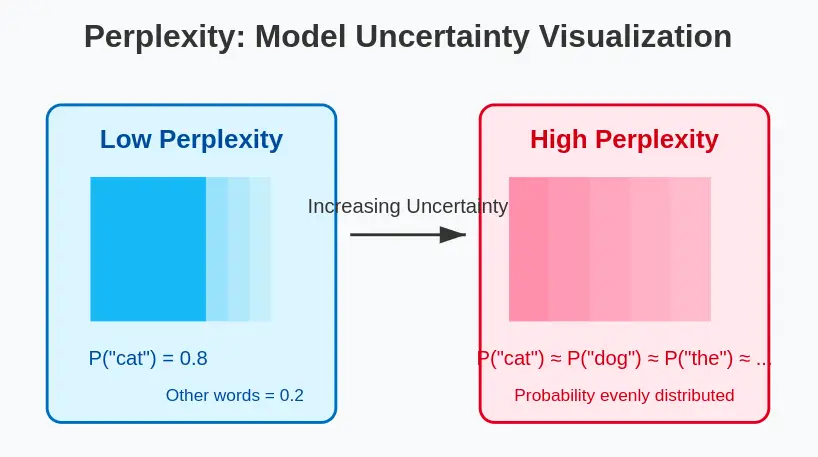
To put it more intuitively:
- Low perplexity: The model is confident and accurate in its predictions about what words come next in a sequence.
- High perplexity: The model is uncertain and struggles to predict the next words in a sequence.
Think of perplexity as answering the question: “On average, how many different words could plausibly follow each word in this text, according to the model?” A perfect model would assign a probability of 1 to each correct word, resulting in a perplexity of 1 (the minimum possible value). Real models, however, distribute probability across multiple possible words, resulting in higher perplexity.
Quick Check: If a language model assigns equal probability to 10 possible next words at each step, what would its perplexity be? (Answer: Exactly 10)
How Does Perplexity Work?
Perplexity works by measuring how well a language model predicts a test set. The process involves:
- Training a language model on a corpus of text
- Evaluating the model on unseen data (the test set)
- Calculating how likely the model thinks the test data is
The fundamental idea is to use the model to assign a probability to each word in the test sequence, given the preceding words. These probabilities are then combined to produce a single perplexity score.
For example, consider the sentence “The cat sat on the mat”:
- The model calculates P(“cat” | “The”)
- Then P(“sat” | “The cat”)
- Then P(“on” | “The cat sat”)
- And so on…
These probabilities are combined to get the overall likelihood of the sentence, which is then converted to perplexity.
How is Perplexity Calculated?
Let’s dive into the mathematics behind perplexity. For a language model, perplexity is defined as the exponential of the average negative log-likelihood:
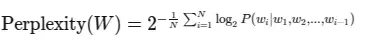
Where:
- $W$ is the test sequence $(w_1, w_2, …, w_N)$
- $N$ is the number of words in the sequence
- $P(w_i|w_1, w_2, …, w_{i-1})$ is the conditional probability of the word $w_i$ given all previous words
Alternatively, if we use the chain rule of probability to express the joint probability of the sequence, we get:
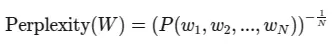
Where $P(w_1, w_2, …, w_N)$ is the joint probability of the entire sequence.
Let’s break down these formulas step by step:
- We calculate the probability of each word given its context (previous words)
- We take the logarithm (typically base 2) of each probability
- We average these log probabilities across the entire sequence
- We take the negative of this average (since log probabilities are negative)
- Finally, we compute 2 raised to this power
The resulting value is the perplexity score.
Try It: Consider a simple model that assigns P(“the”)=0.2, P(“cat”)=0.1, P(“sat”)=0.05 for “The cat sat”. Calculate the perplexity of this sequence. (We’ll show the solution in the implementation section)
Alternate Representations of Perplexity Metric
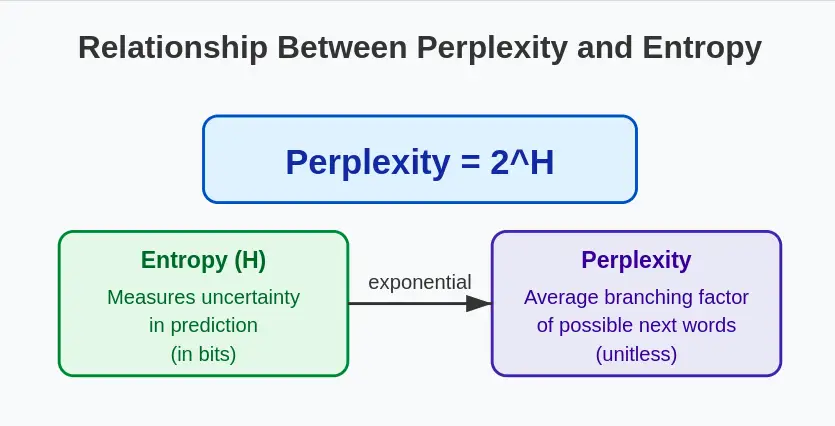
1. Perplexity in Terms of Entropy
Perplexity is directly related to the information-theoretic concept of entropy. If we denote the entropy of the probability distribution as $H$, then:
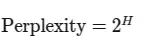
This relationship highlights that perplexity is essentially measuring the average uncertainty in predicting the next word in a sequence. The higher the entropy (uncertainty), the higher the perplexity.
2. Perplexity as a Multiplicative Inverse
Another way to understand the Perplexity Metric is as the inverse of the geometric mean of the word probabilities:
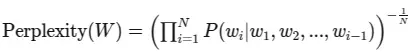
This formulation emphasizes that perplexity is inversely related to the model’s confidence in its predictions. As the model becomes more confident (higher probabilities), the perplexity decreases.
Implementation of Perplexity Metric from Scratch in Python
Let’s implement perplexity calculation in Python to solidify our understanding:
import numpy as np
from collections import Counter, defaultdict
class NgramLanguageModel:
def __init__(self, n=2):
self.n = n
self.context_counts = defaultdict(Counter)
self.context_totals = defaultdict(int)
def train(self, corpus):
"""Train the language model on a corpus"""
# Add start and end tokens
tokens = ['<s>'] * (self.n - 1) + corpus + ['</s>']
# Count n-grams
for i in range(len(tokens) - self.n + 1):
context = tuple(tokens[i:i+self.n-1])
word = tokens[i+self.n-1]
self.context_counts[context][word] += 1
self.context_totals[context] += 1
def probability(self, word, context):
"""Calculate probability of word given context"""
if self.context_totals[context] == 0:
return 1e-10 # Smoothing for unseen contexts
return (self.context_counts[context][word] + 1) / (self.context_totals[context] + len(self.context_counts))
def sequence_probability(self, sequence):
"""Calculate probability of entire sequence"""
tokens = ['<s>'] * (self.n - 1) + sequence + ['</s>']
prob = 1.0
for i in range(len(tokens) - self.n + 1):
context = tuple(tokens[i:i+self.n-1])
word = tokens[i+self.n-1]
prob *= self.probability(word, context)
return prob
def perplexity(self, test_sequence):
"""Calculate perplexity of a test sequence"""
N = len(test_sequence) + 1 # +1 for the end token
log_prob = 0.0
tokens = ['<s>'] * (self.n - 1) + test_sequence + ['</s>']
for i in range(len(tokens) - self.n + 1):
context = tuple(tokens[i:i+self.n-1])
word = tokens[i+self.n-1]
prob = self.probability(word, context)
log_prob += np.log2(prob)
return 2 ** (-log_prob / N)
# Let's test our implementation
def tokenize(text):
"""Simple tokenization by splitting on spaces"""
return text.lower().split()
# Example usage
corpus = tokenize("the cat sat on the mat the dog chased the cat the cat ran away")
test = tokenize("the cat sat on the floor")
model = NgramLanguageModel(n=2)
model.train(corpus)
print(f"Perplexity of test sequence: {model.perplexity(test):.2f}")This implementation creates a basic n-gram language model with add-one smoothing for handling unseen words or contexts. Let’s analyze what’s happening in the code:
- We define an NgramLanguageModel class that stores counts of contexts and words.
- The train method processes a corpus and builds the n-gram statistics.
- The probability method calculates P(word|context) with basic smoothing.
- The sequence_probability method computes the joint probability of a sequence.
- Finally, the perplexity method calculates the perplexity as defined by our formula.
Output
Perplexity of test sequence: 129.42
Example and Output
Let’s run through a complete example with our implementation:
# Training corpus
train_corpus = tokenize("the cat sat on the mat the dog chased the cat the cat ran away")
# Test sequences
test_sequences = [
tokenize("the cat sat on the mat"),
tokenize("the dog sat on the floor"),
tokenize("a bird flew through the window")
]
# Train a bigram model
model = NgramLanguageModel(n=2)
model.train(train_corpus)
# Calculate perplexity for each test sequence
for i, test in enumerate(test_sequences):
ppl = model.perplexity(test)
print(f"Test sequence {i+1}: '{' '.join(test)}'")
print(f"Perplexity: {ppl:.2f}")
print()Output
Test sequence 1: 'the cat sat on the mat'
Perplexity: 6.15
Test sequence 2: 'the dog sat on the floor'
Perplexity: 154.05
Test sequence 3: 'a bird flew through the window'
Perplexity: 28816455.70
Note how the perplexity increases as we move from test sequence 1 (which appears verbatim in the training data) to sequence 3 (which contains many words not seen in training). This demonstrates how perplexity reflects model uncertainty.
Implementing Perplexity Metric in NLTK
For practical applications, you might want to use established libraries like NLTK, which provide more sophisticated implementations of language models and perplexity calculations:
import nltk
from nltk.lm import Laplace
from nltk.lm.preprocessing import padded_everygram_pipeline
from nltk.tokenize import word_tokenize
import math
# Download required resources
nltk.download('punkt')
# Prepare the training data
train_text = "The cat sat on the mat. The dog chased the cat. The cat ran away."
train_tokens = [word_tokenize(train_text.lower())]
# Create n-grams and vocabulary
n = 2 # Bigram model
train_data, padded_vocab = padded_everygram_pipeline(n, train_tokens)
# Train the model using Laplace smoothing
model = Laplace(n) # Laplace (add-1) smoothing to handle unseen words
model.fit(train_data, padded_vocab)
# Test sentence
test_text = "The cat sat on the floor."
test_tokens = word_tokenize(test_text.lower())
# Prepare test data with padding
test_data = list(nltk.ngrams(test_tokens, n, pad_left=True, pad_right=True,
left_pad_symbol='<s>', right_pad_symbol='</s>'))
# Compute perplexity manually
log_prob_sum = 0
N = len(test_data)
for ngram in test_data:
prob = model.score(ngram[-1], ngram[:-1]) # P(w_i | w_{i-1})
log_prob_sum += math.log2(prob) # Avoid log(0) due to smoothing
# Compute final perplexity
perplexity = 2 ** (-log_prob_sum / N)
print(f"Perplexity (Laplace smoothing): {perplexity:.2f}")Output: Perplexity (Laplace smoothing): 8.33
In natural language processing (NLP), perplexity measures how well a language model predicts a sequence of words. A lower perplexity score indicates a better model. However, Maximum Likelihood Estimation (MLE) models suffer from the out-of-vocabulary (OOV) problem, assigning zero probability to unseen words, leading to infinite perplexity.
To solve this, we use Laplace smoothing (Add-1 smoothing), which assigns small probabilities to unseen words, preventing zero probabilities. The corrected code implements a bigram language model using NLTK’s Laplace class instead of MLE. This ensures a finite perplexity score, even when the test sentence contains words not present in training.
This technique is crucial in building robust n-gram models for text prediction and speech recognition.
Advantages of Perplexity
Perplexity offers several advantages as an evaluation metric for language models:
- Interpretability: Perplexity has a clear interpretation as the average branching factor of the prediction task.
- Model-Agnostic: It can be applied to any probabilistic language model that assigns probabilities to sequences.
- No Human Annotations Required: Unlike many other evaluation metrics, perplexity doesn’t require human-annotated reference texts.
- Efficiency: It’s computationally efficient to calculate, especially compared to metrics that require generation or sampling.
- Historical Precedent: As one of the oldest metrics in language modeling, perplexity has established benchmarks and a rich research history.
- Enables Direct Comparison: Models with the same vocabulary can be directly compared based on their perplexity scores.
Limitations of Perplexity
Despite its widespread use, perplexity has several important limitations:
- Vocabulary Dependency: Perplexity scores are only comparable between models that use the same vocabulary.
- Not Aligned with Human Judgment: Lower perplexity doesn’t always translate to better quality in human evaluations.
- Limited for Open-ended Generation: Perplexity evaluates how well a model predicts specific text, not how coherent, diverse, or interesting its generations are.
- No Semantic Understanding: A model could achieve low perplexity by memorizing n-grams without true understanding.
- Task-Agnostic: Perplexity doesn’t measure task-specific performance (e.g., question answering, summarization).
- Issues with Long-Range Dependencies: Traditional implementations of perplexity struggle with evaluating long-range dependencies in text.
Overcoming Limitations Using LLM-as-a-Judge
To address the limitations of perplexity, researchers have developed alternative evaluation approaches, including using large language models as judges (LLM-as-a-Judge):
- Principle: Use a more powerful LLM to evaluate the outputs of another language model.
- Implementation:
- Generate text using the model being evaluated
- Provide this text to a “judge” LLM along with evaluation criteria
- Have the judge LLM score or rank the generated text
- Advantages:
- Can evaluate aspects like coherence, factuality, and relevance
- More aligned with human judgments
- Can be customized for specific evaluation criteria
- Example Implementation:
def llm_as_judge(generated_text, reference_text=None, criteria="coherence and fluency"):
"""Use a large language model to judge generated text"""
# This is a simplified example - in practice, you'd call an actual LLM API
if reference_text:
prompt = f"""
Please evaluate the following generated text based on {criteria}.
Reference text: {reference_text}
Generated text: {generated_text}
Score from 1-10 and provide reasoning.
"""
else:
prompt = f"""
Please evaluate the following generated text based on {criteria}.
Generated text: {generated_text}
Score from 1-10 and provide reasoning.
"""
# In a real implementation, you would call your LLM API here
# response = llm_api.generate(prompt)
# return parse_score(response)
# For demonstration purposes only:
import random
score = random.uniform(1, 10)
return scoreThis approach complements perplexity by providing human-like judgments of text quality across multiple dimensions.
Practical Applications
Perplexity finds applications in various NLP tasks:
- Language Model Evaluation: Comparing different LM architectures or hyperparameter settings.
- Domain Adaptation: Measuring how well a model adapts to a specific domain.
- Out-of-Distribution Detection: Identifying text that doesn’t match the training distribution.
- Data Quality Assessment: Evaluating the quality of training or test data.
- Text Generation Filtering: Using perplexity to filter out low-quality generated text.
- Anomaly Detection: Identifying unusual or anomalous text patterns.
Comparison with Other LLM Evaluation Metrics
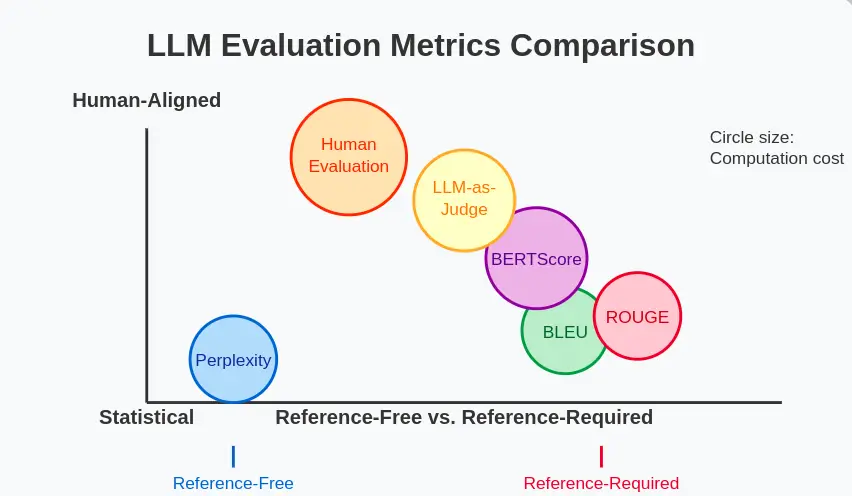
Let’s compare perplexity with other popular evaluation metrics for language models:
| Metric | What It Measures | Advantages | Limitations |
| Perplexity | Prediction accuracy | No reference needed, efficient | Vocabulary dependent, not aligned with human judgment |
| BLEU | N-gram overlap with reference | Good for translation, summarization | Requires reference, poor for creativity |
| ROUGE | Recall of n-grams from reference | Good for summarization | Requires reference, focuses on overlap |
| BERTScore | Semantic similarity using contextual embeddings | Better semantic understanding | Computationally intensive |
| Human Evaluation | Various aspects as judged by humans | Most reliable for quality | Expensive, time-consuming, subjective |
| LLM-as-Judge | Various aspects as judged by an LLM | Flexible, scalable | Depends on judge model quality |
To choose the right metric, consider:
- Task: What aspect of language generation are you evaluating?
- Availability of References: Do you have reference texts?
- Computational Resources: How efficient does the evaluation need to be?
- Interpretability: How important is it to understand the metric?
A hybrid approach often works best—combining perplexity for efficiency with other metrics for comprehensive evaluation.
Conclusion
Perplexity Metric has long served as a key metric for evaluating language models, offering a clear, information-theoretic measure of how well a model predicts text. Despite its limits—like poor alignment with human judgment—it remains useful when combined with newer methods, such as reference-based scores, embedding similarities, and LLM-based evaluations.
As models grow more advanced, evaluation will likely shift toward hybrid approaches that blend perplexity’s efficiency with more human-aligned metrics.
The bottom line: treat perplexity as one signal among many, knowing both its strengths and its blind spots.
Challenge for You: Try implementing perplexity calculation for your own text corpus! Use the code provided in this article as a starting point, and experiment with different n-gram sizes, smoothing techniques, and test sets. How does changing these parameters affect the perplexity scores?






